Навигация
Метод Хемминга
3.1 Метод Хемминга
Метод Хемминга обладает достоинствами, связанными с простотой и относительно небольшой погрешностью. Существует в двух модификациях. Базовый алгоритм (А-метод Хемминга) применяется для прогнозирования относительно стабильных или слабо изменяющихся динамических рядов, имеющих фиксированную структуру.
![]() ,
,
где ![]() – прогнозное значение;
– прогнозное значение;
![]() - значение функции;
- значение функции;
![]() - порядковый номер элемента, входящего в состав исследуемого объекта;
- порядковый номер элемента, входящего в состав исследуемого объекта;
![]() - время запаздывания или исследование обрабатываемых данных (реализация функций объекта);
- время запаздывания или исследование обрабатываемых данных (реализация функций объекта);
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() - коэффициенты настройки, задаваемые жестко, в виде числа.
- коэффициенты настройки, задаваемые жестко, в виде числа.
Для каждого ряда коэффициенты задаются индивидуально. Число коэффициентов всегда не четное. Сумма всех коэффициентов всегда должна быть равной 1 (![]() ).
).
Наиболее удачными, по мнению Хемминга, являются коэффициенты для 3 и 5 слагаемых (таблица 3.2).
Таблица 3.2
| А1 | А2 | А3 | А4 | А5 | |
| для трех | 0,60 | 0,30 | 0,10 | ||
| для пяти | 0,65 | 0,15 | 0,10 | 0,04 | 0,01 |
Данный алгоритм прошел апробацию и достаточно точно прогнозирует переменные различного рода технологических и транспортных операций в нормальном режиме эксплуатации. Однако при применении в случае нештатного и аварийного режимов производства имеет место значительная погрешность, т.е. больше 15%.
Исследования показали, что для увеличения адаптивных возможностей требуется методика настройки коэффициентов, алгоритм которой и включает В-метод Хемминга.
Идея заключается в следующем: в фиксированный момент времени t1 (в который обнаружилось превышение порога погрешности в 5%) рассматривается автокорреляционная функция (АКФ) ряда ![]() . При этом оценивается величина вклада каждой из компонент
. При этом оценивается величина вклада каждой из компонент ![]() в t2, и рассчитываются соответствующие коэффициенты:
в t2, и рассчитываются соответствующие коэффициенты:
Шаг 1: оценивается величина площади под АКФ
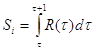 ;
;
Шаг 2: коэффициенты рассчитываются по формуле
![]() .
.
Модифицированный метод проверялся на реальных данных нестационарной динамики, и погрешности не превышали 5-10%, что вполне приемлемо для подобных задач.
Решение:
Результаты моделирования по методу Хэмминга представлены в таблице 3.3.
Таблица 3.3
|
|
|
|
|
| 1 | 50,0 | 50,000 | 0,00 |
| 2 | 53,0 | 53,000 | 0,00 |
| 3 | 56,5 | 54,800 | 1,70 |
| 4 | 53,5 | 54,350 | 0,85 |
| 5 | 51,0 | 52,300 | 1,30 |
| 6 | 54,0 | 53,050 | 0,95 |
| 7 | 53,5 | 53,400 | 0,10 |
| 8 | 60,0 | 57,450 | 2,55 |
| 9 | 59,0 | 58,750 | 0,25 |
| 10 | 60,0 | 59,700 | 0,30 |
| 11 | 61,0 | 60,500 | 0,50 |
| 12 | 62,0 | 61,500 | 0,50 |
| 13 | 58,0 | 59,500 | 1,50 |
| 14 | 57,0 | 57,800 | 0,80 |
| 15 | 57,5 | 57,400 | 0,10 |
| 16 | 59,5 | 58,650 | 0,85 |
| 17 | 60,5 | 59,900 | 0,60 |
| 18 | 61,0 | 60,700 | 0,30 |
| 19 | 62,0 | 61,550 | 0,45 |
| 20 | 62,5 | 62,200 | 0,30 |
| 21 | 61,855 | ||
| 22 | 61,928 | ||
| 23 | 61,933 | ||
| 24 | 61,924 |
Прогнозные значение на основе базового алгоритма Хэмминга (А-метод ):
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
На основе полученных данных построим график прогнозирования по адаптивной модели Хемминга (рисунок 2)
Рисунок 2
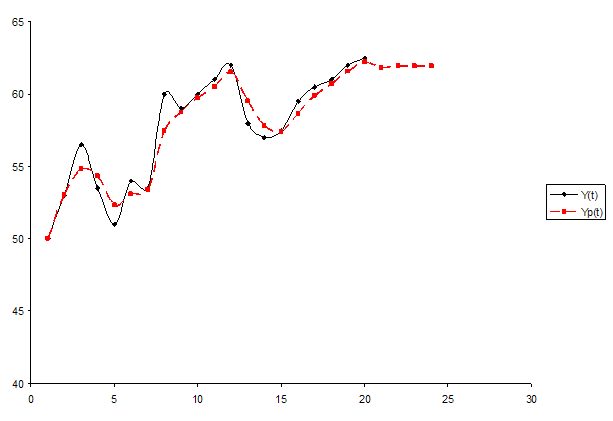
Оценим адекватность модели с помощью коэффициента детерминации. Для этого рассчитаем
![]() ,
,
остальные расчеты представлены в таблице 3.4.
Таблица 3.4
|
|
|
|
| 50,0 | 0,000 | 57,381 |
| 53,0 | 0,000 | 20,931 |
| 56,5 | 2,890 | 1,156 |
| 53,5 | 0,722 | 16,606 |
| 51,0 | 1,690 | 43,231 |
| 54,0 | 0,903 | 12,781 |
| 53,5 | 0,010 | 16,606 |
| 60,0 | 6,503 | 5,881 |
| 59,0 | 0,063 | 2,031 |
| 60,0 | 0,090 | 5,881 |
| 61,0 | 0,250 | 11,731 |
| 62,0 | 0,250 | 19,581 |
| 58,0 | 2,250 | 0,181 |
| 57,0 | 0,640 | 0,331 |
| 57,5 | 0,010 | 0,006 |
| 59,5 | 0,723 | 3,706 |
| 60,5 | 0,360 | 8,556 |
| 61,0 | 0,090 | 11,731 |
| 62,0 | 0,203 | 19,581 |
| 62,5 | 0,090 | 24,256 |
|
| 17,735 | 282,138 |
Коэффициент детерминации находится по формуле:
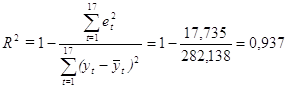 |
Похожие работы
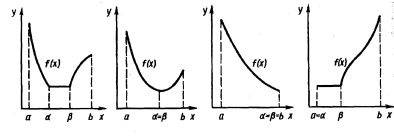
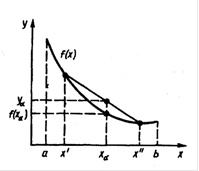
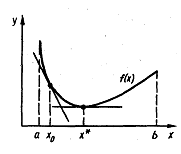
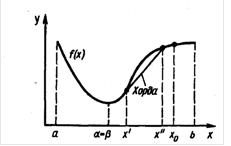
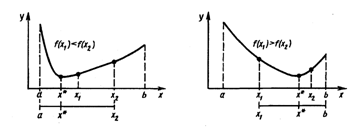
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
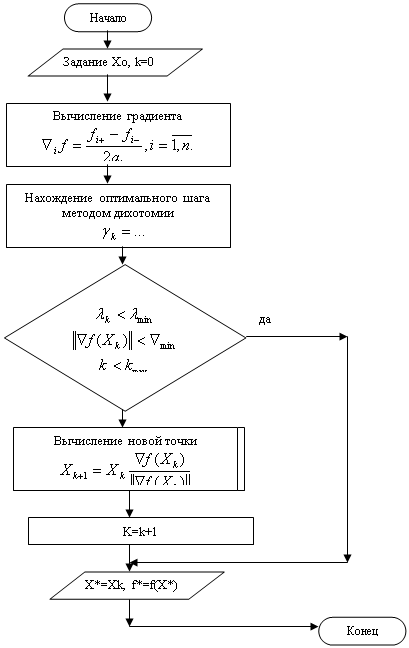
... : т.е. . Для определения координат точки Х1 нужно выбрать значение шага . Получим : Из соотношения (,)=0 имеем: (-3-3)(-3)+(1+)=10+10=0 откуда = Задание 4 ПРИМЕНЕНИЕ ГРАДИЕНТНЫХ МЕТОДОВ ДЛЯ ОПТИМИЗАЦИИ НА ЭВМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ Цель задания: приобрести практические навыки разработки алгоритмов и программ оптимизации математических моделей градиентным методом. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...

0 комментариев