Навигация
Стимулирование и мотивация как функции управления
5 Стимулирование и мотивация как функции управления
1. Задача стимулирования для одноэлементной системы.
Руководитель поручает рабочему производство продукции, используя следующую систему стимулирования: ![]() , где α – ставка оплаты единицы произведенной агентом продукции. Цена, по которой центр продаёт продукцию, p=1000 руб. Затраты агента, выраженные в денежной форме:
, где α – ставка оплаты единицы произведенной агентом продукции. Цена, по которой центр продаёт продукцию, p=1000 руб. Затраты агента, выраженные в денежной форме: ![]() Определить параметр системы стимулирования α.
Определить параметр системы стимулирования α.
Решение:
Запишем целевую функцию центра:
(3.1.1)
и целевую функцию агента:
(3.1.2)
Задача стимулирования формулируется:
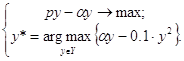 (3.1.3)
(3.1.3)
(3.1.4)
Данная задача решается в 2 этапа. На первом этапе из выражения (3.1.4) определяется реакция агента как аналитическая зависимость от параметра системы стимулирования центра α . На втором этапе полученная аналитическая зависимость подставляется в формулу (3.1.3), получается задача безусловной оптимизации. Решая эту задачу, определим параметр системы стимулирования α.
Первый этап. Найдем реакцию агента из решения оптимизационной задачи (3.1.4). Для этого продифференцируем выражение (3.1.4) по y и приравняем к нулю:
Решая уравнение, определим реакцию агента:
Второй этап. Подставим реакцию агента в целевую функцию (3.1.3):
Вычислим первую производную и приравняем к нулю:
Решая уравнение, определим параметр α:
Ответ: параметр системы стимулирования равен 500.
2. Задача стимулирования для многоэлементной системы со слабосвязанными агентами.
Руководитель поручает работу бригаде, состоящей из двух рабочих. Центр использует пропорциональную систему стимулирования: ![]() , где
, где ![]() – ставка оплаты единицы произведенной i-м агентом продукции. Известна функция затрат каждого агента:
– ставка оплаты единицы произведенной i-м агентом продукции. Известна функция затрат каждого агента: ![]()
Рыночная цена, по которой продается продукция р=1000 руб., фонд заработной платы бригады R=20000 руб. Определить параметры системы стимулирования ![]() и
и ![]() .
.
Решение
Сформулируем задачу стимулирования:
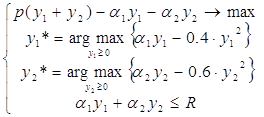 |
(3.2.1)
(3.2.2)
(3.2.3)
(3.2.4)
Первый этап. Из выражения (3.2.2) и (3.2.3) определим реакцию агентов.
Для нахождения экстремума функции одной переменной продифференцируем функции и приравняем к нулю:
Из решения уравнений следует:
Второй этап. Подставив![]() и
и ![]() в выражение для целевой функции центра (3.2.1) и ограничение (3.2.4), получим задачу на условный экстремум:
в выражение для целевой функции центра (3.2.1) и ограничение (3.2.4), получим задачу на условный экстремум:
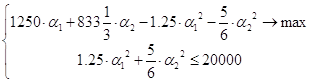 |
Для ее решения применим метод множителей Лагранжа. Запишем функцию Лагранжа:
Найдём частные производные от функции Лагранжа по неизвестным ![]() ,
,![]() и
и ![]() :(3.2.5)
:(3.2.5)
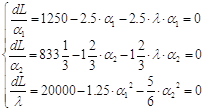 |
(3.2.6)
(3.2.7)
Выразим из (3.2.5) и (3.2.6) неизвестные ![]() ,
,![]() :
:
Получилось, что параметры функций стимулирования для обоих агентов одинаковы. Из ограничения (3.2.7) определяем параметр системы стимулирования:
![]()
![]() Ответ: Параметры системы стимулирования и равны между собой и равны 30,98.
Ответ: Параметры системы стимулирования и равны между собой и равны 30,98.
Похожие работы
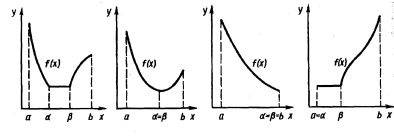
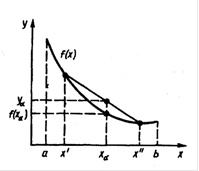
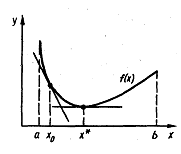
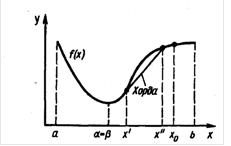
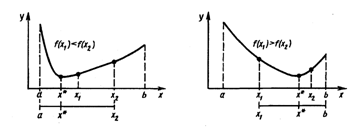
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
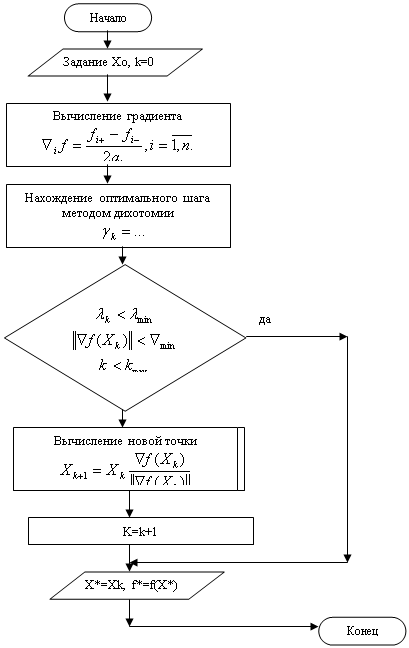
... : т.е. . Для определения координат точки Х1 нужно выбрать значение шага . Получим : Из соотношения (,)=0 имеем: (-3-3)(-3)+(1+)=10+10=0 откуда = Задание 4 ПРИМЕНЕНИЕ ГРАДИЕНТНЫХ МЕТОДОВ ДЛЯ ОПТИМИЗАЦИИ НА ЭВМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ Цель задания: приобрести практические навыки разработки алгоритмов и программ оптимизации математических моделей градиентным методом. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
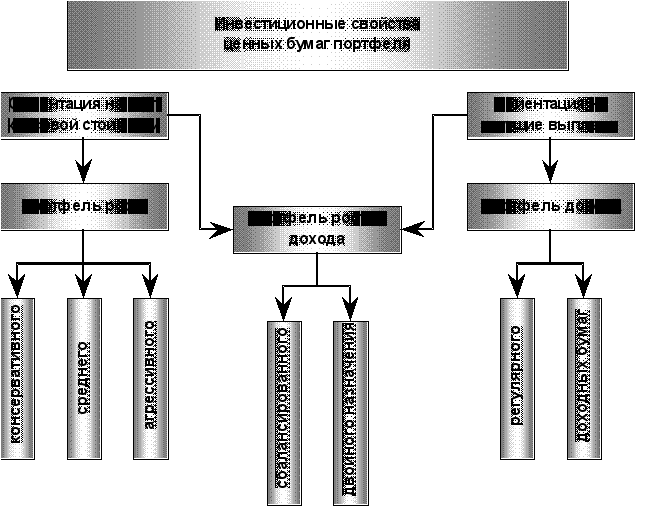
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...

0 комментариев