Моделирование систем массового обслуживания
Графы состояний СМО
Уравнения Колмогорова
Процессы «рождения – гибели»
Экономико-математическая постановка задач массового обслуживания
Одноканальная СМО с отказами в обслуживании
Многоканальная СМО с отказами в обслуживании
Модель многофазной системы обслуживания туристов
Одноканальная СМО с ограниченной длиной очереди
Одноканальная СМО с неограниченной очередью
Многоканальная СМО с ограниченной длиной очереди
Многоканальная СМО с неограниченной очередью
Анализ системы массового обслуживания супермаркета
Навигация
Многоканальная СМО с отказами в обслуживании
Моделирование систем массового обслуживания
93262
знака
21
таблица
4
изображения
3.2 Многоканальная СМО с отказами в обслуживании
В коммерческой деятельности примерами многоканальных СМО являются офисы коммерческих предприятий с несколькими телефонными каналами, бесплатная справочная служба по наличию в авто магазинах самых дешевых автомобилей в Москве имеет 7 телефонных номеров, а дозвониться и получить справку, как известно, очень трудно.
Следовательно, авто магазины теряют клиентов, возможность увеличить количество проданных автомобилей и выручку от продаж, товарооборот, прибыль.
Туристические фирмы по продаже путевок имеют два, три, четыре и более каналов, как, например, фирма Express-Line.
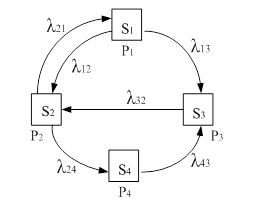
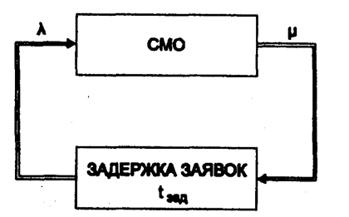
Рассмотрим многоканальную СМО с отказами в обслуживании на рис. 3.2, на вход которой поступает пуассоновский поток заявок с интенсивностью λ.
λ λ
λ λ λ
|
|
S0|
|
|
|
| Sn |
μ 2μ kμ (k+1)μ nμ
Рис. 3.2. Размеченный граф состояний многоканальной СМО с отказами
Поток обслуживания в каждом канале имеет интенсивность μ. По числу заявок СМО определяются ее состояния Sk, представленные в виде размеченного графа:
S0 – все каналы свободны k=0,
S1 – занят только один канал, k=1,
S2 – заняты только два канала, k=2,
Sk – заняты k каналов,
Sn – заняты все n каналов, k= n.
Состояния многоканальной СМО меняются скачкообразно в случайные моменты времени. Переход из одного состояния, например S0 в S1, происходит под воздействием входного потока заявок с интенсивностью λ, а обратно – под воздействием потока обслуживания заявок с интенсивностью μ. Для перехода системы из состояния Skв Sk-1 безразлично, какой именно из каналов освободиться, поэтому поток событий, переводящий СМО, имеет интенсивность kμ, следовательно, поток событий, переводящий систему из Snв Sn-1, имеет интенсивность nμ. Так формулируется классическая задача Эрланга, названная по имени датского инженера – математика- основателя теории массового обслуживания.
Случайный процесс, протекающий в СМО, представляет собой частный случай процесса «рождения- гибели» и описывается системой дифференциальных уравнений Эрланга, которые позволяют получить выражения для предельных вероятностей состояния рассматриваемой системы, называемые формулами Эрланга:
.
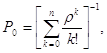
Вычислив все вероятности состояний n – канальной СМО с отказами р0 , р1, р2, …,рk,…, рn, можно найти характеристики системы обслуживания.
Вероятность отказа в обслуживании определяется вероятностью того, что поступившая заявка на обслуживание найдет все n каналов занятыми, система будет находиться в состоянии Sn:
k=n.
В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому
Ротк+Робс=1
На этом основании относительная пропускная способность опредляется по формуле
Q = Pобс= 1-Ротк=1-Рn
Абсолютную пропускную способность СМО можно определить по формуле
А=λ*Робс
Вероятность обслуживания, или доля обслуженных заявок, определяет относительную пропускную способность СМО, которая может быть определена и по другой формуле:
Из этого выражения можно определить среднее число заявок, находящихся под обслуживанием, или, что же самое, среднее число занятых обслуживанием каналов
Коэффициент занятости каналов обслуживанием определятся отношением среднего числа занятых каналов к их общему числу
Вероятность занятости каналов обслуживанием, которая учитывает среднее время занятости tзан и простоя tпр каналов, определяется следующим образом:
Из этого выражения можно определить среднее время простоя каналов
Среднее время пребывания заявки в системе в установившемся режиме определятся формулой Литтла
Тсмо= nз/λ.
Похожие работы
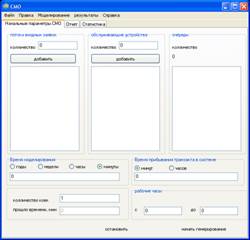
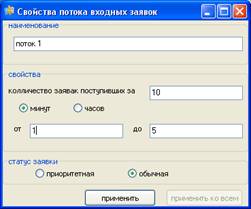
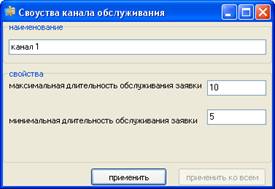
... как точки на временной оси. Для достижения основной цели моделирования достаточно наблюдать систему в моменты реализации основных событий. Рассмотрим пример одноканальной системы массового обслуживания. Целью имитационного моделирования подобной системы является определение оценок ее основных характеристик, таких, как среднее время пребывания заявки в очереди, средняя длина очереди и доля ...
... каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных ...
... 6. Петухов О.А. , Морозов А.В. , Петухова Е.О. Моделирование системное, имитационное, аналитическое. Учебное пособие – Санкт-Петербург 2008 7. Норенков И.П., Федорук Е.В.Имитационное моделирование систем массового обслуживания. Методические указания – Москва 1999 8. Кутузов О.И., Татарникова Т.М., Петров К.О. Распределенные информационные системы управления. Учебное пособие – Санкт-Петербург ...
... *0,1*25 – 1*,09 = 2148,2 ден.ед. Таким образом, максимальная прибыль достигается при установлении трех телефонных линий. Программа имитационного моделирования для оптимального режима работы примет вид: имитационный моделирование массовый обслуживание Результаты расчетов функциональных характеристик СМО: Характеристика Значение l 1/0,67 = 1,5 зв./мин. m 60/2=30 зв./мин. ...
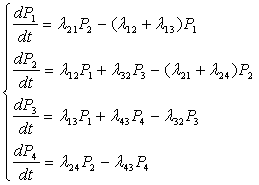
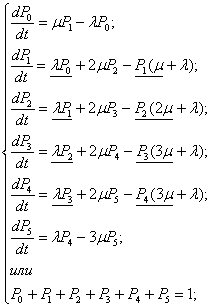
0 комментариев