АНАЛІЗ МЕТОДІВ ТА ПРИЙОМІВ ДОСЛІДЖЕННЯ ФІНАНСОВОЇ ДІЯЛЬНОСТІ
Кратні (моделі розподілу), наприклад вищенаведена формула продуктивності праці [28]
Графічні прийоми пов'язані, передусім, із геометричним зображенням функціональної залежності за допомогою ліній на площині
Аналіз методів теорії синергетики
Мета та задачі дослідження
Методика побудови математичних моделей показників фінансової стійкості
Методика комп’ютерного моделювання
РОЗРОБКА МАТЕМАТИЧНИХ МОДЕЛЕЙ ФІНАНСОВОГО СТАНУ ТА СТІЙКОСТІ БАНКУ
Розробка математичних моделей динаміки зміни коефіцієнтів фінансової стійкості банка
Розробка математичної моделі динаміки зміни коефіцієнта фінансового важеля
Розробка математичної моделі динаміки зміни коефіцієнта участі власного капіталу у формуванні активів
Розробка математичної моделі динаміки зміни коефіцієнта мультиплікатора капіталу
Організація збору і передачі первинної інформації
Технічне забезпечення
ОХОРОНА ПРАЦІ
Вимоги до приміщень, обладнаними робочими місцями з комп'ютерною технікою
Вимоги до організації робочого місця користувача ПЭВМ
Навигация
Розробка математичної моделі динаміки зміни коефіцієнта фінансового важеля
Підвищення ефективності діяльності ПриватБанку на основі теорії синергетики
199453
знака
24
таблицы
50
изображений
3.2.2 Розробка математичної моделі динаміки зміни коефіцієнта фінансового важеля
В якості вихідних даних обраний такий показник фінансової стійкості, як коефіцієнт фінансового важеля, який розкриває здатність банку залучати кошти на фінансовому ринку. Розрахунок цього показника представлен у додатку А.
На основі представленої методики у розділі 2.2 розробляються математичні моделі різних типів. Представимо таблицю 3.14 з порівняльною оцінкою отриманих моделей та оптимальною моделлю.
Таблиця 3.14 – Порівняльна оцінка моделей динаміки зміни коефіцієнта фінансового важеля
| Тип залежності |
| Математична модель | |
| Лінійна | 1150,79 | Х*=-0,41*t+26,03 | |
| Параболічна | 6803,96 | X*=58,45-3,55*t+0,06t2 | |
| Гіперболічна | 972,07 | X*=14,83+5,02*(1/t) | |
| Напівлогарифмічна | 22872,60 | X*=98,75-61,45*logt | |
| Мінімальна | 972,07 | X*=14,83+5,02*(1/t) |
Результати розрахунків показників точності і адекватності між досліджуваними ознаками представлені в таблиці 3.15
Таблиця 3.15 – Розрахунок показників точності і адекватності
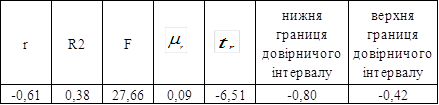
Отримані результати свідчать про те, що сума квадратів відхилень, отриманого значення Xi* (апроксимуючого значення) від заданого значення Xi, мінімальна у випадку побудови гіперболічного поліному. Таким чином, найбільш точним поліномом є гіпербола, яка має таку математичну модель: X*=14,83+5,02*(1/t).
Розрахунок коефіцієнта кореляції говорить о наявності оберненого зв’язку між досліджуваними ознаками з середньою щільністю коефіцієнта фінансового важеля від часу (-0,61).
Отже, в обстеженій сукупності показників коефіцієнта фінансового важеля у 38% варіації здатність банку залучати кошти на фінансовому ринку пояснюється різним часовим періодом. Істотність зв’язку коефіцієнта детермінації R2 перевірили за допомогою таблиці критерію F для 5%-ного рівня значущості. Критичне значення Fт(0,95)=5,32 значно менше від фактичного 5,32<27,66, що підтверджує істотність кореляційного зв’язку між досліджуваними ознаками.
При достатньо великому числі спостережень коефіцієнт кореляції можна вважати достовірним, тому що він перевищує свою помилку в більше ніж 3 рази, а отже зв’язок між коефіцієнтом фінансового важеля (здатність банку залучати кошти на фінансовому ринку) та часом доведений.
Двірничий інтервал: -0,80<r(-0,61)<-0,42.
Усе це дає підставу вважати, що обчислений лінійний коефіцієнт кореляції достатньо точно характеризує щільність зв’язку між досліджуваними ознаками.
0 комментариев