Розробка математичної моделі динаміки зміни коефіцієнта мультиплікатора капіталу

3.2.6 Розробка математичної моделі динаміки зміни коефіцієнта мультиплікатора капіталу

В якості вихідних даних обраний такий показник фінансової стійкості, як коефіцієнт мультиплікатора капіталу, який характеризує ступінь покриття активів (акціонерним) капіталом. Розрахунок цього показника представлен у додатку А.

На основі представленої методики у розділі 2.2 розробляються математичні моделі різних типів. Представимо таблицю 3.22 з порівняльною оцінкою отриманих моделей та оптимальною моделлю.

Результати розрахунків показників точності і адекватності між досліджуваними ознаками представлені в таблиці 3.23

Таблиця 3.22 – Порівняльна оцінка моделей динаміки зміни коефіцієнта мультиплікатору капіталу

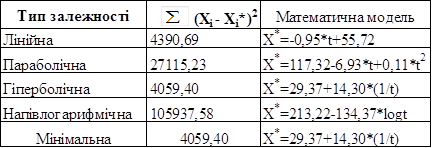
Таблиця 3.23 – Розрахунок показників точності і адекватності

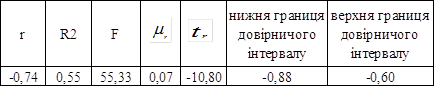
Отримані результати свідчать про те, що сума квадратів відхилень, отриманого значення X_i^* (апроксимуючого значення) від заданого значення X_i, мінімальна у випадку побудови гіперболічного поліному. Таким чином, найбільш точним поліномом є гіпербола, яка має таку математичну модель: X^*= 29,37+14,30*(1/t).

Розрахунок коефіцієнта кореляції говорить о наявності оберненого зв’язку між досліджуваними ознаками з тісною щільністю коефіцієнта мультиплікатора капіталу від часу (-0,74).

Отже, в обстеженій сукупності показників досліджуваного коефіцієнта у 55% варіації ступінь покриття активів (акціонерним) капіталом пояснюється різним часовим періодом. Істотність зв’язку коефіцієнта детермінації R² перевірили за допомогою таблиці критерію F для 5%-ного рівня значущості. Критичне значення F_т(0,95)=5,32 значно менше від фактичного 5,32<55,33, що підтверджує істотність кореляційного зв’язку між досліджуваними ознаками.

При достатньо великому числі спостережень коефіцієнт кореляції можна вважати достовірним, тому що він перевищує свою помилку в більше ніж 3 рази, а отже зв’язок між коефіцієнтом достатності капіталу та часом доведений.

Двірничий інтервал: -0,60<r(-0,74)<-0,88.

Усе це дає підставу вважати, що обчислений лінійний коефіцієнт кореляції достатньо точно характеризує щільність зв’язку між досліджуваними ознаками.

3.3 Комп’ютерне моделювання фінансової стійкості

1) Досліджувані показники фінансової стійкості ПриватБанку розраховані за формулами 2.1 -2.6, наведеними у розділі 2.1, та представлені у додатку А.

2) Установа має нормальну стійкість фінансового стану, яка гарантує його платоспроможність, але є можливість промоделювати деякі показники, щоб вона набула абсолютної стійкості.

3) Коефіцієнт надійності – співвідношення власного капіталу до залучених коштів. Мінімально допустиме його значення складає не менше 5%. Даний показник за досліджуваний період 2005 -2008 роки лише з лютого по жовтень 2005 року був нижче оптимального значення, тобто банк мав високий рівень залежності від залучених коштів, але на протязі всього подальшого часу знаходився в нормі. Тому проводити комп’ютерне моделювання цього показника немає потреби.

4) Показник фінансового важеля – співвідношення зобов’язань банку і капіталу. Він має максимально допустиме співвідношення 1:20. Показник знаходиться нижче указаного співвідношення, а це свідчить про те, що банк не проявляє активності у залученні вільних коштів на фінансовому ринку, тому що має високе забезпечення власними. Виходячи з цього, проводити комп’ютерне моделювання показника фінансового важеля також немає потреби.

5) Коефіцієнт участі власного капіталу у формуванні активів або достатність капіталу – співвідношення капіталу і загальних активів. Оптимальне значення цього показника має бути не менше 10%. Розраховане значення не досягає цього обмеження, тобто банк не має достатнього сформованого власного капіталу в активізації та покритті різних ризиків, але воно має поступовий ріст, що вже говорить про наявність позитивної тенденції. Для досягнення абсолютної стійкості банка за цим показником необхідно провести моделювання.

а) дослідження зміни коефіцієнта достатності капіталу від зміни капіталу

В даному випадку розглянемо поведінку коефіцієнта участі власного капіталу у формуванні активів при незмінному значенні загальних активів та варіації капіталу. За досліджуваний період часу (2005-2008 роки) капітал банку змінювався від 280 193 221,29 і до 1 365 510 804,78 гривень. Побудуємо графік (рис. 3.5), на якому зобразимо досліджуваний коефіцієнт в динаміці в залежності від росту капіталу, а також червону лінію показника (оптимальне значення).

З рисунка можна зробити висновок про те, що коефіцієнт знаходиться в нормі при числовому значенні капіталу від 979 400 104,95 і до 1 021 688 770,43 грн. Таким чином, указаний грошовий інтервал являється критичним значенням капіталу, тому що більші числові значення призводять до росту коефіцієнта достатності капіталу, а менші – к його падінню. Значить, для досягнення абсолютної стійкості банка за цим показником необхідне зростання капіталу.

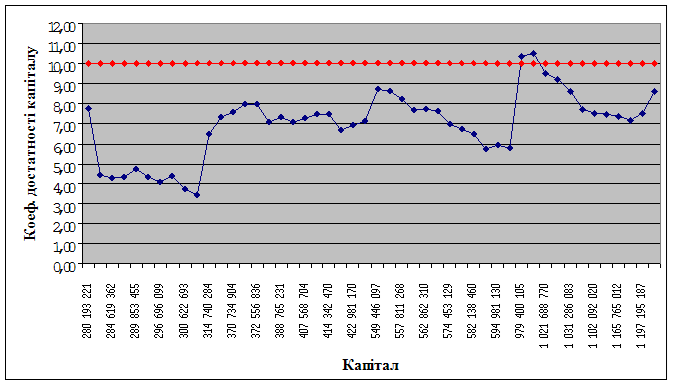
Рисунок 3.5 – Залежність коефіцієнта достатності капіталу від росту капіталу

б) дослідження зміни коефіцієнта достатності капіталу від зміни загальних активів

Розглянемо поведінку коефіцієнта участі власного капіталу у формуванні активів при незмінному значенні капіталу та варіації загальних активів. За досліджуваний період часу (2005-2008 роки) загальні активи банку змінювалися від 3 610 522 710,02 і до 16 692 673 778,10 гривень. Побудуємо графік (рис. 3.6), на якому зобразимо досліджуваний коефіцієнт в динаміці в залежності від росту загальних активів, а також червону лінію показника (оптимальне значення).

З рисунка можна зробити висновок про те, що коефіцієнт знаходиться в нормі при числовому значенні загальних активів від 10 323 838 576,79 і до 10 938 880 583,31 грн. Таким чином, указаний грошовий інтервал являється критичним значенням загальних активів, тому що менші числові значення призводять до росту коефіцієнта достатності капіталу, а більші – к його падінню. Значить, для досягнення абсолютної стійкості банка за цим показником необхідне зменшення загальних активів.

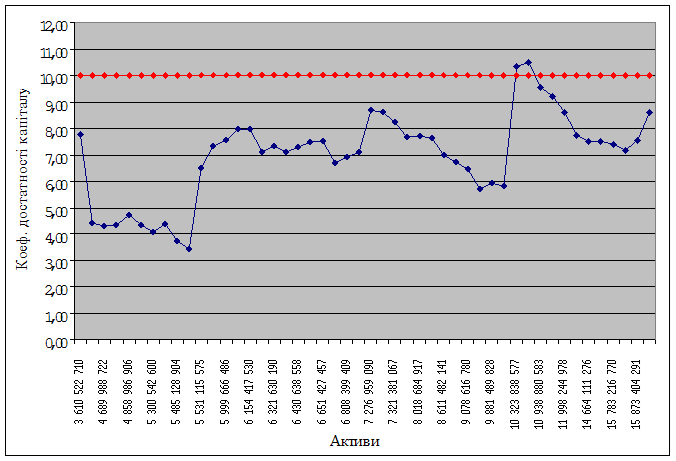
Рисунок 3.6 – Залежність коефіцієнта достатності капіталу від росту загальних активів

в) дослідження зміни коефіцієнта достатності капіталу від одночасної зміни власного капіталу та загальних активів.

Розглянемо поведінку коефіцієнта участі власного капіталу у формуванні активів при варіюванні значень капіталу та загальних активів. Як вже встановлено для росту коефіцієнта необхідне зростання капіталу та зменшення загальних активів. Таким чином, побудуємо графік (рис. 3.7), на якому зобразимо поведінку коефіцієнта при збільшенні капіталу та зменшенні загальних активів від знайденого критичного діапазону значень та припустимо невизначений часовий інтервал.

З отриманих результатів робимо висновок про те, що за досліджуваним коефіцієнтом банк буде мати абсолютну стійкість у випадку зростання капіталу та зниження загальних активів на основі зросту коефіцієнта участі власного капіталу у формування активів.

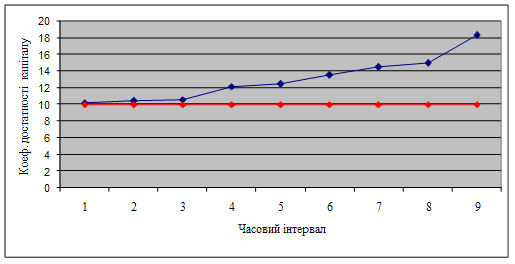
Рисунок 3.7 – Моделювання коефіцієнта участі власного капіталу у формуванні активів від зміни капіталу та загальних активів

6) Коефіцієнт захищеності власного капіталу – співвідношення капіталізованих активів (основні засоби та нематеріальні активи) і капіталу. При розрахунку показника за досліджуваний період виявлено його перемінне зростання, що свідчить про зростання захищеності власного капіталу зростаючим вкладенням його також у свої власні капіталізовані активи. Це свідчить про добру тенденцію, але взагалі показник коефіцієнта остався на одному рівні, тому для абсолютної стійкості банку за цим показником проведемо моделювання.

а) дослідження зміни коефіцієнта захищеності власного капіталу від зміни капіталу

В даному випадку розглянемо поведінку коефіцієнта захищеності власного капіталу при незмінному значенні капіталізованих активів та варіації капіталу. За досліджуваний період часу (2005-2008 роки) капітал банку змінювався від 280 193 221,29 і до 1 365 510 804,78 гривень. Побудуємо графік (рис. 3.8), на якому зобразимо досліджуваний коефіцієнт в динаміці в залежності від росту капіталу.

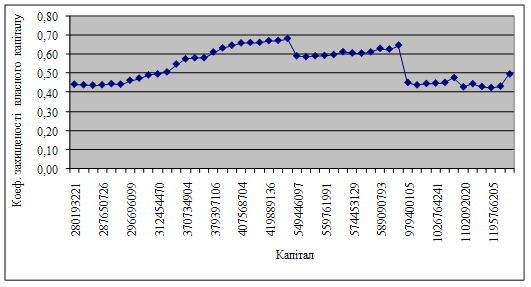
Рисунок 3.8 – Залежність коефіцієнта захищеності капіталу від росту капіталу

З рисунка можна зробити висновок про те, що коефіцієнт має ріст при грошовому значенні капіталу від 414 342 469,97 і до 425 876 358,63 грн. Таким чином, указаний грошовий інтервал являється критичним значенням капіталу, тому що менші числові значення призводять до росту коефіцієнта захищеності капіталу, а більші – к його падінню. Значить, для досягнення абсолютної стійкості банка за цим показником необхідне зменшення капіталу.

б) дослідження зміни коефіцієнта захищеності власного капіталу від зміни капіталізованих активів

Розглянемо поведінку коефіцієнта захищеності власного капіталу при незмінному значенні капіталу та варіації капіталізованих активів. За досліджуваний період часу (2005-2008 роки) капіталізовані активи банку змінювалися від 123 395 197,36 і до 676 969 060,10 гривень. Побудуємо графік (рис. 3.9), на якому зобразимо досліджуваний коефіцієнт в динаміці в залежності від росту капіталізованих активів.

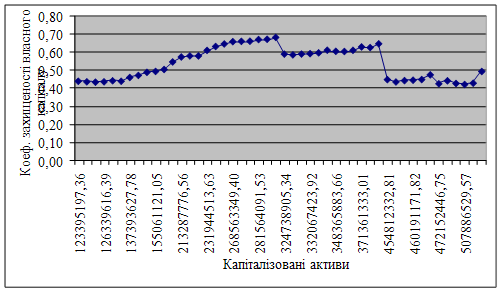
Рисунок 3.9 – Залежність коефіцієнта захищеності власного капіталу від росту капіталізованих активів

З рисунка можна зробити висновок про те, що коефіцієнт має ріст в грошовому значенні капіталізованих активів від 271 360 668,61 і до 290 651 807,34 грн. Таким чином, указаний грошовий інтервал являється критичним значенням капіталізованих активів, тому що більші числові значення призводять до росту коефіцієнта захищеності власного капіталу, а менші – к його падінню. Значить, для досягнення абсолютної стійкості банка за цим показником необхідне збільшення капіталізованих активів.

в) дослідження зміни коефіцієнта захищеності власного капіталу від одночасної зміни власного капіталу та капіталізованих активів

Розглянемо поведінку досліджуваного коефіцієнта при варіюванні значень капіталу та капіталізованих активів. Як вже встановлено для росту коефіцієнта необхідне зростання капіталізованих активів та зменшення капіталу іншими словами темп росту капіталізованих активів повинен перевищувати темп росту капіталу. Таким чином, побудуємо графік (рис. 3.10), на якому зобразимо поведінку коефіцієнта при збільшенні капіталізованих активів та зменшенні капіталу від знайденого критичного діапазону значень та припустимо невизначений часовий інтервал.

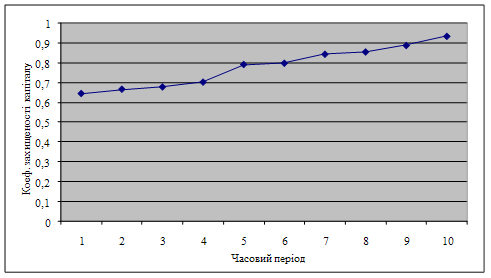
Рисунок 3.10 – Моделювання коефіцієнта захищеності власного капіталу від зміни капіталу та капіталізованих активів

З отриманих результатів робимо висновок про те, що за досліджуваним коефіцієнтом банк буде мати абсолютну стійкість у випадку зростання капіталізованих активів та зниження капіталу на основі зросту коефіцієнта захищеності власного капіталу.

7) Коефіцієнт захищеності дохідних активів власним капіталом – співвідношення капіталу за мінусом недохідних активів та збитків і дохідних активів. Для того, щоб банк посилював захист дохідних активів мобільним власним капіталом, необхідне зростання показника.

а) дослідження зміни коефіцієнта захищеності дохідних активів власним капіталом від зміни капіталу;

В даному випадку розглянемо поведінку досліджуваного коефіцієнта при незмінному значенні недохідних та дохідних активів та варіації капіталу. За досліджуваний період часу (2005-2008 роки) капітал банку змінювався від 280 193 221,29 і до 1 365 510 804,78 гривень. Побудуємо графік (рис. 3.11), на якому зобразимо досліджуваний коефіцієнт в динаміці в залежності від росту капіталу.

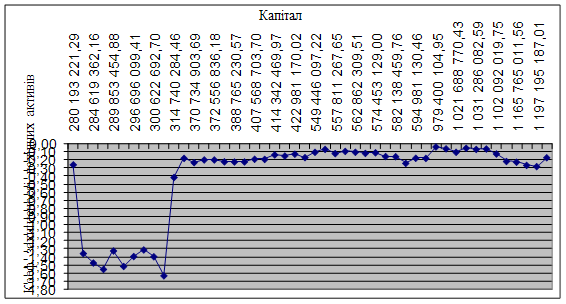Рисунок 3.11 - Залежність коефіцієнта захищеності дохідних активів власним капіталом від росту капіталу

З рисунка можна зробити висновок про те, що коефіцієнт знаходиться в нормі при числовому значенні капіталу від 979 400 104,95 і до 1 021 688 770,43 грн. Таким чином, указаний грошовий інтервал являється критичним значенням капіталу, тому що більші числові значення призводять до росту коефіцієнта захищеності дохідних активів власним капіталом, а менші – к його падінню. Значить, для досягнення абсолютної стійкості банка за цим показником необхідне зростання капіталу.

б) дослідження зміни коефіцієнта захищеності дохідних активів власним капіталом від зміни недохідних активів

Розглянемо поведінку досліджуваного коефіцієнта при незмінному значенні капіталу і дохідних активів та варіації недохідних активів. За досліджуваний період часу (2005-2008 роки) недохідні активи банку змінювалися від 914 466 693,71 і до 5 742 884 541,20 гривень. Побудуємо графік (рис. 3.12), на якому зобразимо коефіцієнт захищеності дохідних активів власним капіталом в динаміці в залежності від росту недохідних активів.

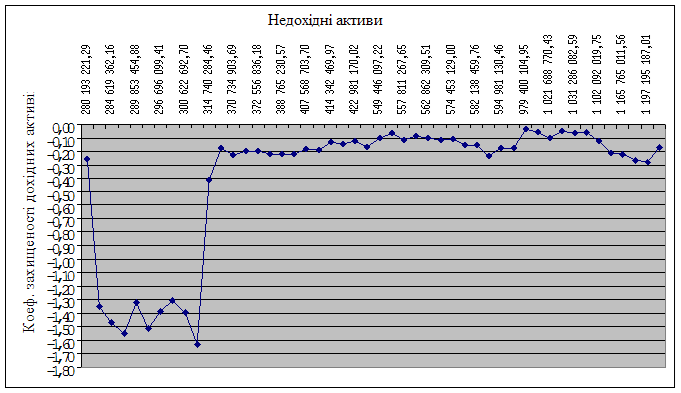
Рисунок 3.12 - Залежність коефіцієнта захищеності дохідних активів власним капіталом від росту недохідних активів

З рисунка можна зробити висновок про те, що коефіцієнт має ріст в грошовому значенні недохідних активів від 3 627 297 962,24 і до 3 990 436 964,64 грн. Таким чином, указаний грошовий інтервал являється критичним значенням недохідних активів, тому що менші числові значення призводять до росту коефіцієнта захищеності дохідних активів власним капіталом, а більші – к його падінню. Значить, для досягнення абсолютної стійкості банка за цим показником необхідне зменшення недохідних активів.

в) дослідження зміни коефіцієнта захищеності дохідних активів власним капіталом від зміни дохідних активів

Розглянемо поведінку досліджуваного коефіцієнта при незмінному значенні капіталу і недохідних активів та варіації дохідних активів. За досліджуваний період часу (2005-2008 роки) дохідні активи банку змінювалися від 2 497 658 105,71 і до 12 396 187 165,61 гривень. Побудуємо графік (рис. 3.13), на якому зобразимо коефіцієнт захищеності дохідних активів власним капіталом в динаміці в залежності від росту дохідних активів.

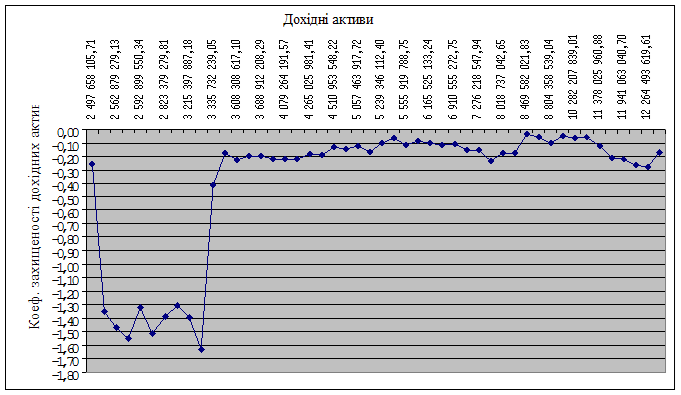
Рисунок 3.13 - Залежність коефіцієнта захищеності дохідних активів власним капіталом від росту дохідних активів

З рисунка можна зробити висновок про те, що коефіцієнт має ріст в грошовому значенні дохідних активів від 8 469 582 021,83 і до 9 609 239 557,89 грн. Таким чином, указаний грошовий інтервал являється критичним значенням дохідних активів, тому що менші числові значення призводять до росту коефіцієнта захищеності дохідних активів власним капіталом, а більші – к його падінню. Значить, для досягнення абсолютної стійкості банка за цим показником необхідне зменшення дохідних активів.

г) дослідження зміни коефіцієнта захищеності дохідних активів власним капіталом від зміни капіталу, дохідних та недохідних активів

Розглянемо поведінку досліджуваного коефіцієнта при варіюванні значень капіталу дохідних та недохідних активів. Як вже встановлено для росту коефіцієнта необхідне зростання капіталу та зменшення недохідних і дохідних активів. Таким чином, побудуємо графік (рис. 3.14), на якому зобразимо поведінку коефіцієнта при збільшенні капіталу та зменшенні недохідних і дохідних активів від знайденого критичного діапазону значень та припустимо невизначений часовий інтервал.

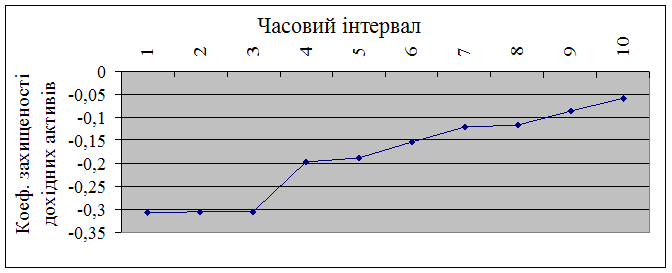
Рисунок 3.14 – Моделювання коефіцієнта захищеності дохідних активів власним капіталом від зміни капіталу, недохідних та дохідних активів

З отриманих результатів робимо висновок про те, що за досліджуваним коефіцієнтом банк буде мати абсолютну стійкість у випадку зростання капіталу та зниження дохідних і недохідних активів на основі зросту коефіцієнта захищеності дохідних активів власним капіталом.

8) Коефіцієнт мультиплікатора капіталу – співвідношення загальних активів і засновницького (акціонерного) капіталу. Оптимальне співвідношення цього показника 12,0 – 15,0 разів. Якщо розраховане значення менше норми, то ступінь покриття активів акціонерним капіталом замала та необхідно, щоб темп зростання акціонерного капіталу перевищував темп зростання активів, а якщо більше – навпаки.

а) дослідження зміни коефіцієнта мультиплікатора капіталу від зміни загальних активів

Розглянемо поведінку досліджуваного коефіцієнта при незмінному значенні засновницького (акціонерного) капіталу та варіації загальних активів. За досліджуваний період часу (2005-2008 роки) загальні активи банку змінювалися від 3 610 522 710,02 і до 16 692 673 778,10 гривень. Побудуємо графік (рис. 3.15), на якому зобразимо коефіцієнт мультиплікатора капіталу в динаміці в залежності від росту загальних активів і червоний (оптимальний) коридор.

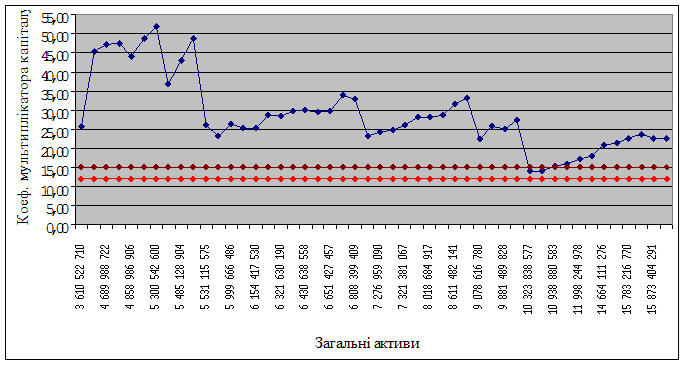
Рисунок 3.15 - Залежність коефіцієнта мультиплікатора капіталу від росту загальних активів

З рисунка можна зробити висновок про те, що коефіцієнт знаходиться в нормі при числовому значенні загальних активів від 10 323 838 576,79 і до 10 938 880 583,31 грн. Таким чином, указаний грошовий інтервал являється критичним значенням загальних активів, тому що менші числові значення призводять до зниження коефіцієнта мультиплікатора капіталу, а більші – к його росту. Значить, для досягнення абсолютної стійкості банка за цим показником необхідне зменшення загальних активів.

б) дослідження зміни коефіцієнта мультиплікатора капіталу від зміни засновницького капіталу

В даному випадку розглянемо поведінку досліджуваного коефіцієнта при незмінному значенні загальних активів та варіації засновницького капіталу. За досліджуваний період часу (2005-2008 роки) акціонерний капітал банку змінювався від 140 000 000,00 до 700 000 000,00 гривень. Побудуємо графік (рис. 3.16), на якому зобразимо коефіцієнт мультиплікатора капіталу в динаміці в залежності від росту засновницького капіталу, а також червоний (оптимальний) коридор.

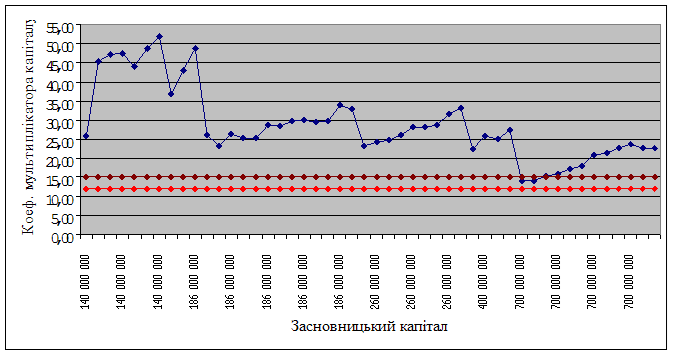
Рисунок 3.16 - Залежність коефіцієнта мультиплікатора капіталу від росту засновницького капіталу

З рисунка можна зробити висновок про те, що коефіцієнт знаходиться в нормі при числовому значенні засновницького капіталу 700 000 000,00 грн. Таким чином, не має можливості указати грошовий інтервал, тому що критичним значенням являється максимальне число акціонерного капіталу, але більші числові значення призводять до росту коефіцієнта мультиплікатора капіталу, а менші – к його падінню. Значить, для досягнення абсолютної стійкості банка за цим показником необхідне зростання засновницького капіталу.

в) дослідження зміни коефіцієнта мультиплікатора капіталу і від одночасної зміни засновницького капіталу та загальних активів

Розглянемо поведінку досліджуваного коефіцієнта при варіюванні значень акціонерного капіталу та загальних активів. Як вже встановлено для оптимального значення коефіцієнта необхідне зростання засновницького капіталу та зменшення загальних активів. Але для того щоб розрахований показник не просто зменшився, а попав в указаний червоний коридор необхідно зафіксувати зменшенні значення загальних активів. Таким чином, побудуємо графік (рис. 3.17), на якому зобразимо поведінку коефіцієнта при збільшенні капіталу та зменшенні загальних активів від знайденого критичного діапазону значень, припустимо невизначений часовий інтервал.

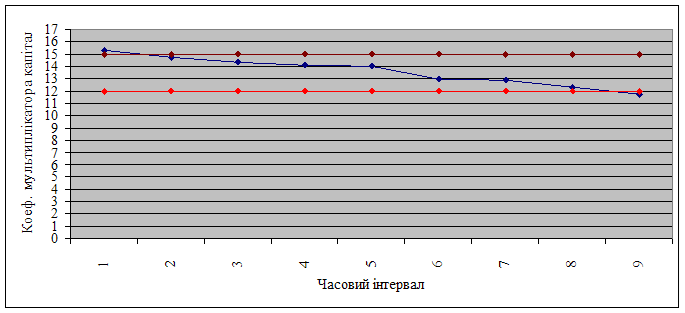
Рисунок 3.17 – Моделювання коефіцієнта мультиплікатора капіталу від зміни засновницького капіталу та загальних активів

З отриманих результатів робимо висновок про те, що за досліджуваним коефіцієнтом банк буде мати абсолютну стійкість у випадку фіксованого значення капіталу 700 000 000,00 грн. та зміни загальних активів від 8 61 482 141,49 до 10 323 838 576,79, тому що коефіцієнт мультиплікатора капіталу буде знаходитись в указаному червоному (оптимальному) коридорі.

4 РОЗРОБКА ІНФОРМАЦІЙНОЇ СИСТЕМИ

4.1 Інформаційне забезпечення

4.1.1 Загальна характеристика інформаційного забезпечення

Інформаційне забезпечення являє собою сукупність проектних рішень по обсягах, розміщенню, формах організації інформації, що циркулює в автоматизованих інформаційних технологіях. Воно містить у собі сукупність показників, довідкових даних, класифікаторів і кодифікаторів інформації, уніфіковані системи документації, спеціально організовані для автоматичного обслуговування, масиви інформації на відповідних носіях, а також персонал, що забезпечує надійність збереження, своєчасність і якість технології обробки інформації [9].

Загальну структуру інформаційного забезпечення ілюструє рисунок 4.1. Важливою складовою інформаційного забезпечення є інформаційна база, що складається з внутрімашинної і внемашинной інформаційної бази.

Машинна інформаційна база – частина інформаційної бази інформаційної системи, що являє собою сукупність інформаційних файлів, що зберігаються в пам'яті ЕОМ і на магнітних носіях.

Машинна інформаційна база складається з інформаційних файлів, що можуть бути організовані у виді окремих незалежних між собою, локальних інформаційних файлів або у виді бази даних, тобто інтегрованої сукупності зв'язаних між собою файлів, якими керує система керування базами даних (СУБД).

Файл – це ідентифікована сукупність логічно зв'язаних між собою даних, що розташовані поза програмою в зовнішній пам'яті і доступні програмі за допомогою спеціальних операцій.

База даних (БД) – це пойменована, структурована сукупність взаємозалежних даних, що характеризують окрему предметну область і знаходяться під керуванням СУБД [5].

Основне функціональне призначення інформаційне забезпечення системи - нагромадження всієї доступної інформації, що передує і супроводжує біржовому процесові, а також генеруємої їм, і видача біржової інформації або результатів аналізу біржового процесу зовнішнім приймачам інформації фондового ринку.

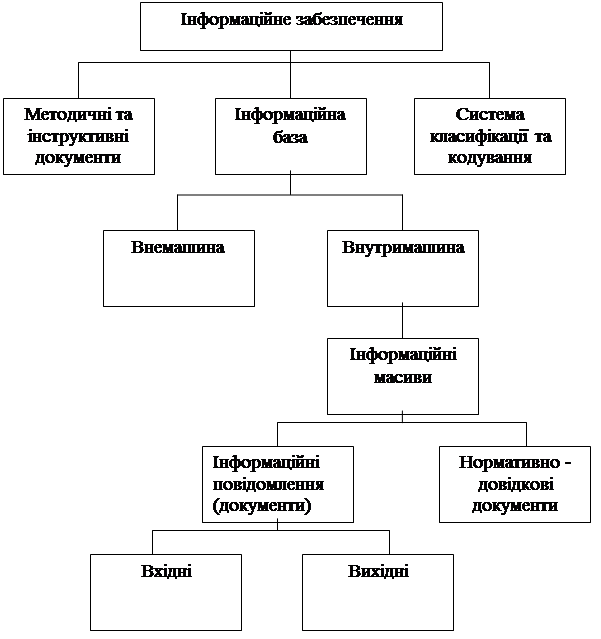
Рисунок 4.1 – Структура інформаційного забезпечення

На вибір СУБД найбільший вплив робить узгодження ряду параметрів середовища реалізації і СУБД [9].

Фактори, що впливають на вибір СУБД:

§     трудомісткість реалізації додатків;

§     вартість експлуатації інформаційної системи;

§     можливість з'єднання розробки БД із раніше виконаними програмними реалізаціями;

§     прогнозовані терміни реалізації інформаційної системи;

§     витрати на навчання персоналу.

Для контролю інформації необхідно вирішити наступні задачі:

·                    створити "динамічну" модель предметної області системи (у якій відповідність БД поточному станові предметної області забезпечується не періодично, а в режимі реального часу);

·                    забезпечити ефективність функціонування, тобто забезпечити вимоги своєчасної реакції системи на запити і відновлення БД;

·                    забезпечити централізоване збереження даних у пам'яті ЕОМ;

·                    забезпечити вибірку з інформаційних масивів даних відповідно заданим критеріям;

·                    забезпечити захист даних від некоректних відновлень, від руйнувань при збоях устаткування і від несанкціонованого доступу.

Ці задачі можна здійснити за допомогою створення єдиного сховища - бази даних і використання засобів СУБД [22].