Навигация
Розробка математичних моделей динаміки зміни коефіцієнтів фінансової стійкості банка
3.2 Розробка математичних моделей динаміки зміни коефіцієнтів фінансової стійкості банка
3.2.1 Розробка математичної моделі динаміки зміни коефіцієнта надійності
Розглянемо запропоновану методику у розділі 2.2 на прикладі одного з показників фінансової стійкості, а саме коефіцієнта надійності.
1) Формуємо масив вихідних даних (табл. 3.7) на основі даних, розрахованих у розділі 2.1 ( додаток А).
де ti- часовий інтервал (з 01.01.01 до 01.12.04р.);
Хi –відповідний показник коефіцієнта надійності.
Таблиця 3.7 – Вихідні данні
| № п/п | ti | Xi | № п/п | ti | Xi | № п/п | ti | Xi |
| 1 | 1 | 8,41 | 17 | 17 | 7,91 | 33 | 33 | 6,91 |
| 2 | 2 | 4,62 | 18 | 18 | 7,62 | 34 | 34 | 6,05 |
| 3 | 3 | 4,50 | 19 | 19 | 7,86 | 35 | 35 | 6,31 |
| 4 | 4 | 4,52 | 20 | 20 | 8,09 | 36 | 36 | 6,16 |
| 5 | 5 | 4,94 | 21 | 21 | 8,10 | 37 | 37 | 11,53 |
| 6 | 6 | 4,53 | 22 | 22 | 7,14 | 38 | 38 | 11,73 |
| 7 | 7 | 4,25 | 23 | 23 | 7,43 | 39 | 39 | 10,53 |
| 8 | 8 | 4,57 | 24 | 24 | 7,64 | 40 | 40 | 10,16 |
| 9 | 9 | 3,90 | 25 | 25 | 9,52 | 41 | 41 | 9,40 |
| 10 | 10 | 3,56 | 26 | 26 | 9,42 | 42 | 42 | 8,38 |
| 11 | 11 | 6,93 | 27 | 27 | 8,98 | 43 | 43 | 8,13 |
| 12 | 12 | 7,91 | 28 | 28 | 8,28 | 44 | 44 | 8,10 |
| 13 | 13 | 8,17 | 29 | 29 | 8,35 | 45 | 45 | 7,98 |
| 14 | 14 | 8,63 | 30 | 30 | 8,26 | 46 | 46 | 7,72 |
| 15 | 15 | 8,63 | 31 | 31 | 7,50 | 47 | 47 | 8,16 |
| 16 | 16 | 7,63 | 32 | 32 | 7,21 | 48 | 48 | 9,42 |
2) Вибір апроксимуючого полінома і його параметрів для коефіцієнта надійності
а) Визначення параметрів та побудова лінійної моделі
Таблиця 3.8 - Процедура розрахунку показників моделі при лінійній апроксимації
| № п/п | ti | Xi | ti2 | Xi * ti | Xi* | (Xi - Xi*)2 |
| 1 | 1 | 8,41 | 1 | 8,41 | 7,45 | 0,92 |
| 2 | 2 | 4,62 | 4 | 9,24 | 7,48 | 8,16 |
| 3 | 3 | 4,50 | 9 | 13,49 | 7,50 | 9,02 |
| 4 | 4 | 4,52 | 16 | 18,08 | 7,52 | 9,02 |
| 5 | 5 | 4,94 | 25 | 24,71 | 7,55 | 6,78 |
| 6 | 6 | 4,53 | 36 | 27,20 | 7,57 | 9,22 |
| 7 | 7 | 4,25 | 49 | 29,75 | 7,59 | 11,17 |
| 8 | 8 | 4,57 | 64 | 36,54 | 7,62 | 9,29 |
| 9 | 9 | 3,90 | 81 | 35,06 | 7,64 | 14,02 |
| 10 | 10 | 3,56 | 100 | 35,64 | 7,66 | 16,80 |
| 11 | 11 | 6,93 | 121 | 76,19 | 7,69 | 0,58 |
| 12 | 12 | 7,91 | 144 | 94,89 | 7,71 | 0,04 |
| 13 | 13 | 8,17 | 169 | 106,22 | 7,73 | 0,19 |
| 14 | 14 | 8,63 | 196 | 120,81 | 7,76 | 0,76 |
| 15 | 15 | 8,63 | 225 | 129,44 | 7,78 | 0,72 |
| 16 | 16 | 7,63 | 256 | 122,03 | 7,80 | 0,03 |
| 17 | 17 | 7,91 | 289 | 134,55 | 7,83 | 0,01 |
| 18 | 18 | 7,62 | 324 | 137,08 | 7,85 | 0,05 |
| 19 | 19 | 7,86 | 361 | 149,40 | 7,87 | 0,00 |
| 20 | 20 | 8,09 | 400 | 161,86 | 7,89 | 0,04 |
| 21 | 21 | 8,10 | 441 | 170,05 | 7,92 | 0,03 |
| 22 | 22 | 7,14 | 484 | 157,06 | 7,94 | 0,64 |
| 23 | 23 | 7,43 | 529 | 170,97 | 7,96 | 0,28 |
| 24 | 24 | 7,64 | 576 | 183,38 | 7,99 | 0,12 |
| 25 | 25 | 9,52 | 625 | 237,97 | 8,01 | 2,27 |
| 26 | 26 | 9,42 | 676 | 245,00 | 8,03 | 1,93 |
| 27 | 27 | 8,98 | 729 | 242,34 | 8,06 | 0,84 |
| 28 | 28 | 8,28 | 784 | 231,80 | 8,08 | 0,04 |
| 29 | 29 | 8,35 | 841 | 242,19 | 8,10 | 0,06 |
| 30 | 30 | 8,26 | 900 | 247,67 | 8,13 | 0,02 |
| 31 | 31 | 7,50 | 961 | 232,52 | 8,15 | 0,42 |
| 32 | 32 | 7,21 | 1024 | 230,65 | 8,17 | 0,93 |
| 33 | 33 | 6,91 | 1089 | 228,19 | 8,20 | 1,64 |
| 34 | 34 | 6,05 | 1156 | 205,75 | 8,22 | 4,70 |
| 35 | 35 | 6,31 | 1225 | 220,89 | 8,24 | 3,73 |
| 36 | 36 | 6,16 | 1296 | 221,67 | 8,27 | 4,44 |
| 37 | 37 | 11,53 | 1369 | 426,53 | 8,29 | 10,49 |
| 38 | 38 | 11,73 | 1444 | 445,66 | 8,31 | 11,67 |
| 39 | 39 | 10,53 | 1521 | 410,80 | 8,34 | 4,83 |
| 40 | 40 | 10,16 | 1600 | 406,43 | 8,36 | 3,25 |
| 41 | 41 | 9,40 | 1681 | 385,55 | 8,38 | 1,04 |
| 42 | 42 | 8,38 | 1764 | 351,86 | 8,40 | 0,00 |
| 43 | 43 | 8,13 | 1849 | 349,43 | 8,43 | 0,09 |
| 44 | 44 | 8,10 | 1936 | 356,29 | 8,45 | 0,13 |
| 45 | 45 | 7,98 | 2025 | 358,88 | 8,47 | 0,25 |
| 46 | 46 | 7,72 | 2116 | 354,94 | 8,50 | 0,61 |
| 47 | 47 | 8,16 | 2209 | 383,40 | 8,52 | 0,13 |
| 48 | 48 | 9,42 | 2304 | 452,01 | 8,54 | 0,76 |
| Сумма | 1176,00 | 361,66 | 38024,00 | 9620,48 | 383,95 | 152,19 |
В результаті рішення системи рівнянь (2.8) обчислюємо значення параметрів a і b і одержуємо поліном при лінійній апроксимації Х*=0,02*t+7,43. Представляємо графічне зображення отриманого рішення на рисунку 3.1.
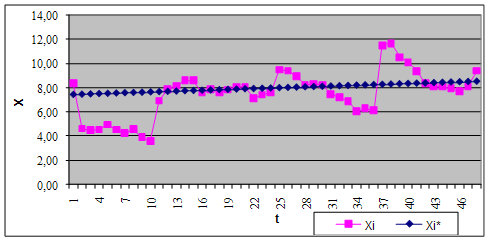
Рисунок 3.1 – Лінійна апроксимація динаміки зміни коефіцієнта надійності – Х*=0,02*t+7,43
На графіку 1 відповідає січень 2005 року, 2 – лютий 2005 року і т.д. до 48 – грудень 2008 року.
б) Визначення параметрів та побудова параболічної моделі
Таблиця 3.9 - Процедура розрахунку показників моделі при параболічній апроксимації
| № п/п | ti | Xi | ti2 | ti3 | ti4 | Xi * ti | Xi * ti2 | Xi* | (Xi - Xi*)2 |
| 1 | 1 | 8,41 | 1 | 1 | 1 | 8,41 | 8,41 | 10,97 | 6,55 |
| 2 | 2 | 4,62 | 4 | 8 | 16 | 9,24 | 18,48 | 10,64 | 36,22 |
| 3 | 3 | 4,50 | 9 | 27 | 81 | 13,49 | 40,47 | 10,32 | 33,91 |
| 4 | 4 | 4,52 | 16 | 64 | 256 | 18,08 | 72,32 | 10,02 | 30,20 |
| 5 | 5 | 4,94 | 25 | 125 | 625 | 24,71 | 123,56 | 9,73 | 22,88 |
| 6 | 6 | 4,53 | 36 | 216 | 1296 | 27,20 | 163,21 | 9,45 | 24,16 |
| 7 | 7 | 4,25 | 49 | 343 | 2401 | 29,75 | 208,27 | 9,19 | 24,37 |
| 8 | 8 | 4,57 | 64 | 512 | 4096 | 36,54 | 292,36 | 8,94 | 19,10 |
| 9 | 9 | 3,90 | 81 | 729 | 6561 | 35,06 | 315,50 | 8,70 | 23,13 |
| 10 | 10 | 3,56 | 100 | 1000 | 10000 | 35,64 | 356,43 | 8,49 | 24,21 |
| 11 | 11 | 6,93 | 121 | 1331 | 14641 | 76,19 | 838,06 | 8,28 | 1,83 |
| 12 | 12 | 7,91 | 144 | 1728 | 20736 | 94,89 | 1138,63 | 8,09 | 0,03 |
| 13 | 13 | 8,17 | 169 | 2197 | 28561 | 106,22 | 1380,87 | 7,91 | 0,07 |
| 14 | 14 | 8,63 | 196 | 2744 | 38416 | 120,81 | 1691,31 | 7,75 | 0,78 |
| 15 | 15 | 8,63 | 225 | 3375 | 50625 | 129,44 | 1941,55 | 7,60 | 1,06 |
| 16 | 16 | 7,63 | 256 | 4096 | 65536 | 122,03 | 1952,52 | 7,46 | 0,03 |
| 17 | 17 | 7,91 | 289 | 4913 | 83521 | 134,55 | 2287,42 | 7,34 | 0,33 |
| 18 | 18 | 7,62 | 324 | 5832 | 104976 | 137,08 | 2467,41 | 7,24 | 0,14 |
| 19 | 19 | 7,86 | 361 | 6859 | 130321 | 149,40 | 2838,64 | 7,14 | 0,52 |
| 20 | 20 | 8,09 | 400 | 8000 | 160000 | 161,86 | 3237,12 | 7,06 | 1,06 |
| 21 | 21 | 8,10 | 441 | 9261 | 194481 | 170,05 | 3571,10 | 7,00 | 1,21 |
| 22 | 22 | 7,14 | 484 | 10648 | 234256 | 157,06 | 3455,39 | 6,95 | 0,04 |
| 23 | 23 | 7,43 | 529 | 12167 | 279841 | 170,97 | 3932,30 | 6,91 | 0,27 |
| 24 | 24 | 7,64 | 576 | 13824 | 331776 | 183,38 | 4401,04 | 6,89 | 0,56 |
| 25 | 25 | 9,52 | 625 | 15625 | 390625 | 237,97 | 5949,29 | 6,88 | 6,94 |
| 26 | 26 | 9,42 | 676 | 17576 | 456976 | 245,00 | 6369,95 | 6,89 | 6,42 |
| 27 | 27 | 8,98 | 729 | 19683 | 531441 | 242,34 | 6543,13 | 6,91 | 4,26 |
| 28 | 28 | 8,28 | 784 | 21952 | 614656 | 231,80 | 6490,36 | 6,95 | 1,78 |
| 29 | 29 | 8,35 | 841 | 24389 | 707281 | 242,19 | 7023,51 | 6,99 | 1,84 |
| 30 | 30 | 8,26 | 900 | 27000 | 810000 | 247,67 | 7430,17 | 7,06 | 1,44 |
| 31 | 31 | 7,50 | 961 | 29791 | 923521 | 232,52 | 7208,24 | 7,13 | 0,13 |
| 32 | 32 | 7,21 | 1024 | 32768 | 1048576 | 230,65 | 7380,88 | 7,22 | 0,00 |
| 33 | 33 | 6,91 | 1089 | 35937 | 1185921 | 228,19 | 7530,20 | 7,33 | 0,17 |
| 34 | 34 | 6,05 | 1156 | 39304 | 1336336 | 205,75 | 6995,45 | 7,45 | 1,95 |
| 35 | 35 | 6,31 | 1225 | 42875 | 1500625 | 220,89 | 7731,22 | 7,58 | 1,62 |
| 36 | 36 | 6,16 | 1296 | 46656 | 1679616 | 221,67 | 7980,02 | 7,73 | 2,47 |
| 37 | 37 | 11,53 | 1369 | 50653 | 1874161 | 426,53 | 15781,76 | 7,89 | 13,22 |
| 38 | 38 | 11,73 | 1444 | 54872 | 2085136 | 445,66 | 16934,98 | 8,07 | 13,39 |
| 39 | 39 | 10,53 | 1521 | 59319 | 2313441 | 410,80 | 16021,20 | 8,26 | 5,18 |
| 40 | 40 | 10,16 | 1600 | 64000 | 2560000 | 406,43 | 16257,11 | 8,46 | 2,88 |
| 41 | 41 | 9,40 | 1681 | 68921 | 2825761 | 385,55 | 15807,41 | 8,68 | 0,52 |
| 42 | 42 | 8,38 | 1764 | 74088 | 3111696 | 351,86 | 14778,00 | 8,91 | 0,29 |
| 43 | 43 | 8,13 | 1849 | 79507 | 3418801 | 349,43 | 15025,55 | 9,16 | 1,07 |
| 44 | 44 | 8,10 | 1936 | 85184 | 3748096 | 356,29 | 15676,82 | 9,42 | 1,75 |
| 45 | 45 | 7,98 | 2025 | 91125 | 4100625 | 358,88 | 16149,70 | 9,69 | 2,96 |
| 46 | 46 | 7,72 | 2116 | 97336 | 4477456 | 354,94 | 16327,39 | 9,98 | 5,14 |
| 47 | 47 | 8,16 | 2209 | 103823 | 4879681 | 383,40 | 18019,67 | 10,29 | 4,53 |
| 48 | 48 | 9,42 | 2304 | 110592 | 5308416 | 452,01 | 21696,43 | 10,60 | 1,41 |
| Сума | 1176 | 362 | 38024 | 1382976 | 53651864 | 9620,48 | 319840,83 | 395,62 | 334,04 |
В результаті рішення системи рівнянь (2.9) обчислюємо значення параметрів a0, a1 і a2 і одержуємо поліном при параболічній апроксимації Х*= 11,32-0,35*t-0,01*t2. Представляємо графічне зображення отриманого рішення на рисунку3.2.
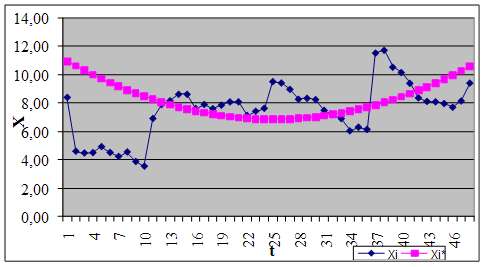
Рисунок 3.2 – Параболічна апроксимація динаміки зміни коефіцієнта надійності - Х*= 11,32-0,35*t-0,01*t2
в) Визначення параметрів та побудова гіперболічної моделі
Таблиця 3.10 - Процедура розрахунку показників моделі при гіперболічній апроксимації
| № п/п | ti | Xi | 1/ti | 1/ti2 | Xi/ti | Xi* | (Xi - Xi*)2 |
| 1 | 1 | 8,41 | 1,00 | 1,00 | 8,41 | 3,22 | 26,99 |
| 2 | 2 | 4,62 | 0,50 | 0,25 | 2,31 | 5,89 | 1,62 |
| 3 | 3 | 4,50 | 0,33 | 0,11 | 1,50 | 6,78 | 5,23 |
| 4 | 4 | 4,52 | 0,25 | 0,06 | 1,13 | 7,23 | 7,34 |
| 5 | 5 | 4,94 | 0,20 | 0,04 | 0,99 | 7,50 | 6,53 |
| 6 | 6 | 4,53 | 0,17 | 0,03 | 0,76 | 7,68 | 9,87 |
| 7 | 7 | 4,25 | 0,14 | 0,02 | 0,61 | 7,80 | 12,62 |
| 8 | 8 | 4,57 | 0,13 | 0,02 | 0,57 | 7,90 | 11,09 |
| 9 | 9 | 3,90 | 0,11 | 0,01 | 0,43 | 7,97 | 16,63 |
| 10 | 10 | 3,56 | 0,10 | 0,01 | 0,36 | 8,03 | 19,96 |
| 11 | 11 | 6,93 | 0,09 | 0,01 | 0,63 | 8,08 | 1,33 |
| 12 | 12 | 7,91 | 0,08 | 0,01 | 0,66 | 8,12 | 0,05 |
| 13 | 13 | 8,17 | 0,08 | 0,01 | 0,63 | 8,16 | 0,00 |
| 14 | 14 | 8,63 | 0,07 | 0,01 | 0,62 | 8,18 | 0,20 |
| 15 | 15 | 8,63 | 0,07 | 0,00 | 0,58 | 8,21 | 0,18 |
| 16 | 16 | 7,63 | 0,06 | 0,00 | 0,48 | 8,23 | 0,37 |
| 17 | 17 | 7,91 | 0,06 | 0,00 | 0,47 | 8,25 | 0,11 |
| 18 | 18 | 7,62 | 0,06 | 0,00 | 0,42 | 8,27 | 0,43 |
| 19 | 19 | 7,86 | 0,05 | 0,00 | 0,41 | 8,29 | 0,18 |
| 20 | 20 | 8,09 | 0,05 | 0,00 | 0,40 | 8,30 | 0,04 |
| 21 | 21 | 8,10 | 0,05 | 0,00 | 0,39 | 8,31 | 0,05 |
| 22 | 22 | 7,14 | 0,05 | 0,00 | 0,32 | 8,32 | 1,40 |
| 23 | 23 | 7,43 | 0,04 | 0,00 | 0,32 | 8,33 | 0,81 |
| 24 | 24 | 7,64 | 0,04 | 0,00 | 0,32 | 8,34 | 0,49 |
| 25 | 25 | 9,52 | 0,04 | 0,00 | 0,38 | 8,35 | 1,36 |
| 26 | 26 | 9,42 | 0,04 | 0,00 | 0,36 | 8,36 | 1,13 |
| 27 | 27 | 8,98 | 0,04 | 0,00 | 0,33 | 8,37 | 0,37 |
| 28 | 28 | 8,28 | 0,04 | 0,00 | 0,30 | 8,38 | 0,01 |
| 29 | 29 | 8,35 | 0,03 | 0,00 | 0,29 | 8,38 | 0,00 |
| 30 | 30 | 8,26 | 0,03 | 0,00 | 0,28 | 8,39 | 0,02 |
| 31 | 31 | 7,50 | 0,03 | 0,00 | 0,24 | 8,39 | 0,80 |
| 32 | 32 | 7,21 | 0,03 | 0,00 | 0,23 | 8,40 | 1,42 |
| 33 | 33 | 6,91 | 0,03 | 0,00 | 0,21 | 8,40 | 2,22 |
| 34 | 34 | 6,05 | 0,03 | 0,00 | 0,18 | 8,41 | 5,56 |
| 35 | 35 | 6,31 | 0,03 | 0,00 | 0,18 | 8,41 | 4,42 |
| 36 | 36 | 6,16 | 0,03 | 0,00 | 0,17 | 8,42 | 5,11 |
| 37 | 37 | 11,53 | 0,03 | 0,00 | 0,31 | 8,42 | 9,65 |
| 38 | 38 | 11,73 | 0,03 | 0,00 | 0,31 | 8,43 | 10,90 |
| 39 | 39 | 10,53 | 0,03 | 0,00 | 0,27 | 8,43 | 4,43 |
| 40 | 40 | 10,16 | 0,03 | 0,00 | 0,25 | 8,43 | 2,98 |
| 41 | 41 | 9,40 | 0,02 | 0,00 | 0,23 | 8,44 | 0,94 |
| 42 | 42 | 8,38 | 0,02 | 0,00 | 0,20 | 8,44 | 0,00 |
| 43 | 43 | 8,13 | 0,02 | 0,00 | 0,19 | 8,44 | 0,10 |
| 44 | 44 | 8,10 | 0,02 | 0,00 | 0,18 | 8,45 | 0,12 |
| 45 | 45 | 7,98 | 0,02 | 0,00 | 0,18 | 8,45 | 0,22 |
| 46 | 46 | 7,72 | 0,02 | 0,00 | 0,17 | 8,45 | 0,54 |
| 47 | 47 | 8,16 | 0,02 | 0,00 | 0,17 | 8,45 | 0,09 |
| 48 | 48 | 9,42 | 0,02 | 0,00 | 0,20 | 8,46 | 0,92 |
| Сума | 1176 | 361,66 | 4,46 | 1,62 | 29,51 | 387,36 | 176,81 |
У результаті рішення системи рівнянь обчислюємо значення параметрів a0 і a1 і одержуємо поліном при гіперболічній апроксимації: X*=8,57-5,35*1/t. Представляємо графічне зображення отриманого рішення на рисунку 3.3
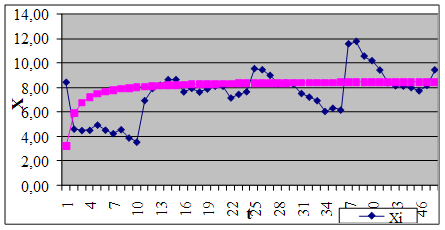
Рисунок 3.3 – Гіперболічна апроксимація динаміки зміни коефіцієнта надійності - X*=8,57-5,35*1/t
г) Визначення параметрів та побудова напівлогарифмічної моделі
Таблиця 3.11 - Процедура розрахунку показників моделі при напівлогарифмічній апроксимації
| № п/п | ti | Xi | Log ti | (log ti)^2 | Xi log ti | Xi* | (Xi - Xi*)2 |
| 1 | 1 | 8,41 | 0,00 | 0,00 | 0,00 | 15,94 | 56,67 |
| 2 | 2 | 4,62 | 0,30 | 0,09 | 1,39 | 14,19 | 91,55 |
| 3 | 3 | 4,50 | 0,48 | 0,23 | 2,15 | 13,16 | 75,10 |
| 4 | 4 | 4,52 | 0,60 | 0,36 | 2,72 | 12,44 | 62,66 |
| 5 | 5 | 4,94 | 0,70 | 0,49 | 3,45 | 11,87 | 48,01 |
| 6 | 6 | 4,53 | 0,78 | 0,61 | 3,53 | 11,41 | 47,29 |
| 7 | 7 | 4,25 | 0,85 | 0,71 | 3,59 | 11,02 | 45,84 |
| 8 | 8 | 4,57 | 0,90 | 0,82 | 4,13 | 10,68 | 37,40 |
| 9 | 9 | 3,90 | 0,95 | 0,91 | 3,72 | 10,39 | 42,13 |
| 10 | 10 | 3,56 | 1,00 | 1,00 | 3,56 | 10,12 | 42,96 |
| 11 | 11 | 6,93 | 1,04 | 1,08 | 7,21 | 9,88 | 8,71 |
| 12 | 12 | 7,91 | 1,08 | 1,16 | 8,53 | 9,66 | 3,07 |
| 13 | 13 | 8,17 | 1,11 | 1,24 | 9,10 | 9,46 | 1,65 |
| 14 | 14 | 8,63 | 1,15 | 1,31 | 9,89 | 9,27 | 0,41 |
| 15 | 15 | 8,63 | 1,18 | 1,38 | 10,15 | 9,09 | 0,22 |
| 16 | 16 | 7,63 | 1,20 | 1,45 | 9,18 | 8,93 | 1,70 |
| 17 | 17 | 7,91 | 1,23 | 1,51 | 9,74 | 8,78 | 0,74 |
| 18 | 18 | 7,62 | 1,26 | 1,58 | 9,56 | 8,63 | 1,04 |
| 19 | 19 | 7,86 | 1,28 | 1,64 | 10,06 | 8,50 | 0,40 |
| 20 | 20 | 8,09 | 1,30 | 1,69 | 10,53 | 8,37 | 0,07 |
| 21 | 21 | 8,10 | 1,32 | 1,75 | 10,71 | 8,24 | 0,02 |
| 22 | 22 | 7,14 | 1,34 | 1,80 | 9,58 | 8,13 | 0,97 |
| 23 | 23 | 7,43 | 1,36 | 1,85 | 10,12 | 8,01 | 0,34 |
| 24 | 24 | 7,64 | 1,38 | 1,90 | 10,55 | 7,91 | 0,07 |
| 25 | 25 | 9,52 | 1,40 | 1,95 | 13,31 | 7,80 | 2,95 |
| 26 | 26 | 9,42 | 1,41 | 2,00 | 13,33 | 7,70 | 2,96 |
| 27 | 27 | 8,98 | 1,43 | 2,05 | 12,85 | 7,61 | 1,87 |
| 28 | 28 | 8,28 | 1,45 | 2,09 | 11,98 | 7,52 | 0,58 |
| 29 | 29 | 8,35 | 1,46 | 2,14 | 12,21 | 7,43 | 0,85 |
| 30 | 30 | 8,26 | 1,48 | 2,18 | 12,19 | 7,34 | 0,84 |
| 31 | 31 | 7,50 | 1,49 | 2,22 | 11,19 | 7,26 | 0,06 |
| 32 | 32 | 7,21 | 1,51 | 2,27 | 10,85 | 7,18 | 0,00 |
| 33 | 33 | 6,91 | 1,52 | 2,31 | 10,50 | 7,10 | 0,03 |
| 34 | 34 | 6,05 | 1,53 | 2,35 | 9,27 | 7,02 | 0,95 |
| 35 | 35 | 6,31 | 1,54 | 2,38 | 9,74 | 6,95 | 0,41 |
| 36 | 36 | 6,16 | 1,56 | 2,42 | 9,58 | 6,88 | 0,52 |
| 37 | 37 | 11,53 | 1,57 | 2,46 | 18,08 | 6,81 | 22,25 |
| 38 | 38 | 11,73 | 1,58 | 2,50 | 18,53 | 6,74 | 24,84 |
| 39 | 39 | 10,53 | 1,59 | 2,53 | 16,76 | 6,68 | 14,86 |
| 40 | 40 | 10,16 | 1,60 | 2,57 | 16,28 | 6,61 | 12,58 |
| 41 | 41 | 9,40 | 1,61 | 2,60 | 15,17 | 6,55 | 8,13 |
| 42 | 42 | 8,38 | 1,62 | 2,63 | 13,60 | 6,49 | 3,56 |
| 43 | 43 | 8,13 | 1,63 | 2,67 | 13,27 | 6,43 | 2,87 |
| 44 | 44 | 8,10 | 1,64 | 2,70 | 13,31 | 6,37 | 2,97 |
| 45 | 45 | 7,98 | 1,65 | 2,73 | 13,18 | 6,32 | 2,75 |
| 46 | 46 | 7,72 | 1,66 | 2,76 | 12,83 | 6,26 | 2,12 |
| 47 | 47 | 8,16 | 1,67 | 2,80 | 13,64 | 6,21 | 3,81 |
| 48 | 48 | 9,42 | 1,68 | 2,83 | 15,83 | 6,15 | 10,65 |
| Сума | 1176 | 362 | 61 | 85 | 481 | 409 | 692 |
В результаті рішення системи рівнянь обчислюємо значення параметрів a0 і a1 і одержуємо поліном при напівлогарифмічній апроксимації: X*=15,94-5,82*logt. Представляємо графічне зображення отриманого рішення на рисунку 3.4.
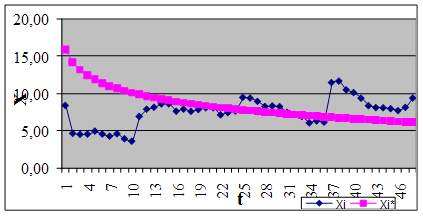
Рисунок 3.4 – Напівлогарифмічна апроксимація динаміки зміни коефіцієнта надійності - X*=15,94-5,82*logt
3) Порівняння значень Xi*, отриманих шляхом застосування кожного з поліномів.
Таблиця 3.12 – Порівняльна оцінка моделей динаміки зміни коефіцієнта надійності
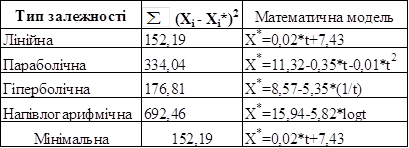
Найбільш точним поліномом являється лінійна модель, яка відповідає емпіричним (заданим) значенням Xi та дає найменше значення цієї суми (152,19).
4) Розрахунок показників точності і адекватності між досліджуваними ознаками
Таблиця 3.13 – Показники точності і адекватності
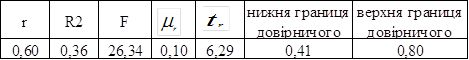
5) Висновки відносно отриманих результатів та визначення оптимальної моделі.
Отримані результати, які наведені в таблиці 3.8, говорять про те, що сума квадратів відхилень, отриманого значення Xi* (апроксимуючого значення) від заданого значення Xi, мінімальна у випадку побудови лінійного поліному. Таким чином, найбільш точним поліномом є лінійна модель, яка має наступну математичну модель: X*=0,02*t+7,43.
Розрахунок коефіцієнта кореляції говорить о наявності прямого зв’язку між досліджуваними ознаками з середньою щільністю коефіцієнта надійності від часу (0,6).
Отже, в обстеженій сукупності показників коефіцієнта надійності 36% варіації рівень залежності банку від залучених коштів пояснюється різним часовим періодом. Істотність зв’язку коефіцієнта детермінації R2 перевірили за допомогою таблиці критерію F для 5%-ного рівня значущості. Критичне значення Fт(0,95)=5,32 значно менше від фактичного 5,32<26,34, що підтверджує істотність кореляційного зв’язку між досліджуваними ознаками.
При достатньо великому числі спостережень коефіцієнт кореляції можна вважати достовірним, тому що він перевищує свою помилку в більше ніж 3 рази, а отже зв’язок між коефіцієнтом надійності (рівнем залежності банку від залучених коштів) та часом доведений.
Двірничий інтервал: 0,41<r(0,60)<0,80.
Усе це дає підставу вважати, що обчислений лінійний коефіцієнт кореляції достатньо точно характеризує щільність зв’язку між досліджуваними ознаками.
Аналогічно робимо розрахунки для інших коефіцієнтів фінансової стійкості.
0 комментариев