Навигация
Методика побудови математичних моделей показників фінансової стійкості
2.2 Методика побудови математичних моделей показників фінансової стійкості
В якості вихідних даних були обрані показники фінансової стійкості, зокрема коефіцієнт надійності, коефіцієнт фінансового важеля, коефіцієнт участі власного капіталу у формуванні активів, коефіцієнт захищеності власного капіталу, коефіцієнт захищеності дохідних активів власним капіталом, коефіцієнт мультиплікатора капіталу, розраховані в розділі 2.1 ( додаток А).
Методика передбачає розробку математичних моделей різних типів і вибір оптимальних моделей по сукупності критеріїв якості і надійності:
1) Сформувати масив вихідних даних:
ti- часовий інтервал (з 01.01.01 до 01.12.04р.);
Хi – відповідний показник коефіцієнта фінансової стійкості.
2) Вибір апроксимуючого полінома і його параметрів для даного тимчасового ряду коефіцієнта фінансової стійкості.
а) У випадку лінійної форми зв’язку результативна ознака змінюється під впливом факторної ознаки рівномірно. Така форма зв’язку виражається рівнянням прямої:
Х*=а*t+b (2.7)
де Х* - вирівняне середнє значення результативної ознаки;
a і b – параметри рівняння.
Параметри рівняння a і b визначаємо методом найменших квадратів складеної і розв’язаної системи двох рівнянь з двома невідомими:
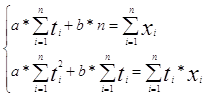 |
(2.8)
де n – число членів в кожному з двох порівнювальних рядів;
![]() - сума значень факторної ознаки;
- сума значень факторної ознаки;
![]() - сума квадратів значень факторної ознаки;
- сума квадратів значень факторної ознаки;
![]() - сума значень результативної ознаки;
- сума значень результативної ознаки;
![]() - сума добутків значень факторної ознаки на значення результативної ознаки [7].
- сума добутків значень факторної ознаки на значення результативної ознаки [7].
Результати розрахунку представляємо у виді таблиці 2.1.
Таблиця 2.1 - Процедура розрахунку показників моделі при лінійній апроксимації
| № п/п | ti | Xi | ti2 | Xi * ti | Xi* | (Xi - Xi*)2 |
| ... | ... | ... | ... | ... | ... | ... |
| Сума | Сума | Сума | Сума | Сума | Сума |
В результаті рішення системи рівнянь обчислюємо значення параметрів a і b і одержуємо поліном при лінійній апроксимації. Представляємо графічне зображення отриманого рішення.
б) Параболічна залежність як форма математичного вираження зв’язків між досліджуваними явищами застосовується в тих випадках, коли із зростанням факторної ознаки відбувається нерівномірне зростання або спадання результативної ознаки.
При знаходженні рівняння зв’язку між ознаками в якості апроксимаційної функції застосовується тип кривої, вираженої у вигляді параболи другого порядку:
X*=a0+a1*t+a2*t2 (2.9)
Параметри a0, a1 і a2 визначаємо по методу найменших квадратів шляхом складання і розв’язку системи нормальних рівнянь [7]:
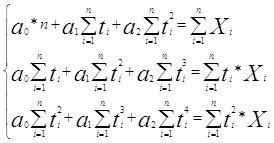 |
(2.10)
Результати розрахунку представимо у виді таблиці 2.2.
Таблиця 2.2 - Процедура розрахунку показників моделі при параболічній апроксимації
| № п/п | ti | Xi | ti2 | ti3 | ti4 | Xi * ti | Xi * ti2 | Xi* | (Xi -Xi*)2 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| Сума | Сума | Сума | Сума | Сума | Сума | Сума | Сума | Сума |
У результаті рішення системи рівнянь обчислюємо значення параметрів a0, a1 і a2 і одержуємо поліном при параболічній апроксимації. Представляємо графічне зображення отриманого рішення.
в) Якщо результативна ознака при збільшенні факторної ознаки спадає, але не безкінечно, а прямує до певного рівня, то для її аналізу застосовується рівняння гіперболи:
(2.11)
Параметри a0 і a1 визначаємо по методу найменших квадратів при рішенні системи рівнянь [7]:
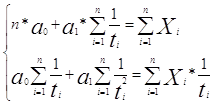 |
(2.12)
Результати розрахунку представимо у виді таблиці 2.3.
Таблиця 2.3 - Процедура розрахунку показників моделі при гіперболічній апроксимації
| № п/п | ti | Xi | 1/ti | 1/ti2 | Xi/ti | Xi* | (Xi - Xi*)2 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| Сума | Сума | Сума | Сума | Сума | Сума | Сума |
У результаті рішення системи рівнянь обчислюємо значення параметрів a0 і a1 і одержуємо поліном при гіперболічній апроксимації. Представляємо графічне зображення отриманого рішення.
г) Вирівнювання за напівлогарифмічною кривою проводяться в тих випадках, коли зі зростанням факторної ознаки середня результативна ознака спочатку до певних меж зростає досить швидко, але пізніше темпи її зростання поступово сповільнюються:
(2.13)
Параметри a0 і a1 визначаємо по методу найменших квадратів при рішенні системи рівнянь [7]:
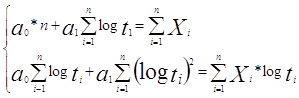 |
(2.14)
Результати розрахунку представляємо у виді таблиці 2.4.
Таблиця 2.4 - Процедура розрахунку показників моделі при напівлогарифмічній апроксимації
| № п/п | ti | Xi | Log ti | (log ti)^2 | Xi log ti | Xi* | (Xi - Xi*)2 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| Сума | Сума | Сума | Сума | Сума | Сума | Сума |
В результаті рішення системи рівнянь обчислюємо значення параметрів a0 і a1 і одержуємо поліном при напівлогарифмічній апроксимації [7]. Представляємо графічне зображення отриманого рішення.
3) Провести, засноване на методі найменших квадратів, порівняння значень Xi*, отриманих шляхом застосування кожного з поліномів. Сутність методу найменших квадратів полягає в тім, що сума квадратів відхилень, отриманого значення Xi* (апроксимуючого значення) від заданого значення Xi, повинна бути мінімальної.
Найбільш точний поліном, що відповідає емпіричним (заданим) значенням Xi, повинний дати найменше значення цієї суми. Для порівняння рекомендується побудувати таблицю 2.5.
Таблиця 2.5 – Порівняльна оцінка моделей
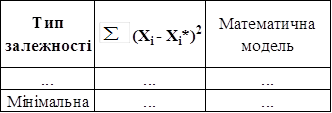
4) Визначення параметрів математичної моделі та розрахунок показників точності і адекватності.
а) Для вимірювання щільності зв’язку і визначення його напрямку використовується коефіцієнта кореляції, який визначається за формулою:
 (2.15)
(2.15)
Величина коефіцієнта лінійної кореляції змінюється у діапазоні: -1 < r < 1. Чим більше | r |, тим сильніше лінійна залежність компонентів t і X.
б) Коефіцієнт детермінації показує яка частка зміни Х пояснюється впливом на нього t. Він визначається як квадрат парного лінійного коефіцієнта кореляції:
![]() (2.16)
(2.16)
де r- коефіцієнт кореляції.
в) Коефіцієнти кореляції, як правило, розраховуються для вибіркових даних. Щоб поширити отримані приватні результати на генеральну сукупність, приходиться допустити деяку помилку, яку можна оцінити за допомогою середньоквадратичної помилки (![]() ):
):
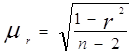 , (2.17)
, (2.17)
де r- коефіцієнт кореляції;
n- обсяг вибіркової сукупності.
При достатньо великому числі спостережень (n>50) коефіцієнт кореляції можна вважати достовірним, якщо він перевищує свою помилку в 3 і більше разів, а якщо він менший 3, то зв’язок між досліджуваними ознаками t і Х не доведений [7].
г) За допомогою середньоквадратичної помилки обчислюють коефіцієнт надійності (tr), що порівнюють з табличним значенням коефіцієнта надійності (tтабл):
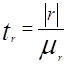 , (2.18)
, (2.18)
де r- коефіцієнт кореляції;
![]() - середньоквадратична помилка.
- середньоквадратична помилка.
Якщо tr > tтабл, то коефіцієнт кореляції вважається значимим [7].
д) Для генерального коефіцієнта кореляції обчислюється довірчий інтервал:
r - ![]() r* tтабл …r +
r* tтабл …r +![]() r* tтабл, (2.19)
r* tтабл, (2.19)
де r- коефіцієнт кореляції;
![]() - середньоквадратична помилка;
- середньоквадратична помилка;
tтабл - табличне значення коефіцієнта кореляції.
є) Адекватність моделі означає, що відповідне рівняння регресії правильне, коректно описує взаємозв'язок між результативною і пояснюючою перемінною. Для перевірки адекватності моделі застосовується статистичний критерій адекватності, що називається критерієм Фішера. Він розраховується по формулі:
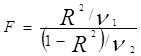 , (2.20)
, (2.20)
де R2- коефіцієнт детермінації;
![]() і
і ![]() — ступеня волі.
— ступеня волі.
![]() = 1
= 1
![]() = n – 2
= n – 2
F порівнюють з табличними значеннями статистики Фішера. Для 5%-ного рівня значущості критичне значення Fт(0,95)=5,32. Якщо F > Fтабл, то модель є адекватною, а якщо менше, те неадекватною [26].
Результати розрахунків показників точності і адекватності між досліджуваними ознаками представляємо у виді таблиці 2.6.
Таблиця 2.6 - Розрахунок показників точності і адекватності

5) Висновки відносно отриманих результатів та визначення оптимальної моделі по сукупності критеріїв якості і надійності.
0 комментариев