Розробка математичної моделі динаміки зміни коефіцієнта участі власного капіталу у формуванні активів

3.2.3 Розробка математичної моделі динаміки зміни коефіцієнта участі власного капіталу у формуванні активів

В якості вихідних даних обраний такий показник фінансової стійкості, як коефіцієнт участі власного капіталу у формуванні активів, який розкриває достатність сформованого власного капіталу в активізації та покритті різних ризиків. Розрахунок цього показника представлен у додатку А.

На основі представленої методики у розділі 2.2 розробляються математичні моделі різних типів. Представимо таблицю 3.16 з порівняльною оцінкою отриманих моделей та оптимальною моделлю.

Таблиця 3.16 – Порівняльна оцінка моделей динаміки зміни коефіцієнта участі власного капіталу у формуванні активів

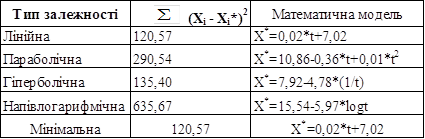
Результати розрахунків показників точності і адекватності між досліджуваними ознаками представлені в таблиці 3.17

Таблиця 3.17 – Розрахунок показників точності і адекватності

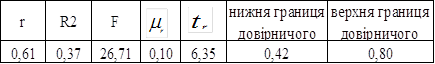
Отримані результати свідчать про те, що сума квадратів відхилень, отриманого значення X_i^* (апроксимуючого значення) від заданого значення X_i, мінімальна у випадку побудови лінійного поліному. Таким чином, найбільш точним поліномом є лінія, яка має таку математичну модель: X^*= 0,02*t+7,02.

Розрахунок коефіцієнта кореляції говорить о наявності прямого зв’язку між досліджуваними ознаками з середньою щільністю коефіцієнта участі власного капіталу у формуванні активів від часу (0,61).

Отже, в обстеженій сукупності показників коефіцієнта фінансового важеля у 37% варіації достатність сформованого власного капіталу в активізації та покритті різних ризиків пояснюється різним часовим періодом. Істотність зв’язку коефіцієнта детермінації R² перевірили за допомогою таблиці критерію F для 5%-ного рівня значущості. Критичне значення F_т(0,95)=5,32 значно менше від фактичного 5,32<26,71, що підтверджує істотність кореляційного зв’язку між досліджуваними ознаками.

При достатньо великому числі спостережень коефіцієнт кореляції можна вважати достовірним, тому що він перевищує свою помилку в більше ніж 3 рази, а отже зв’язок між коефіцієнтом достатності капіталу та часом доведений.

Двірничий інтервал: 0,42<r(0,61)<0,80.

Усе це дає підставу вважати, що обчислений лінійний коефіцієнт кореляції достатньо точно характеризує щільність зв’язку між досліджуваними ознаками.

3.2.4 Розробка математичної моделі динаміки зміни коефіцієнта захищеності власного капіталу

В якості вихідних даних обраний такий показник фінансової стійкості, як коефіцієнт захищеності власного капіталу, який показує яку частину капіталу розміщено в нерухомість (майно). Розрахунок цього показника представлен у додатку А.

На основі представленої методики у розділі 2.2 розробляються математичні моделі різних типів. Представимо таблицю 3.18 з порівняльною оцінкою отриманих моделей та оптимальною моделлю.

Таблиця 3.18 – Порівняльна оцінка моделей динаміки зміни коефіцієнта захищеності власного капіталу

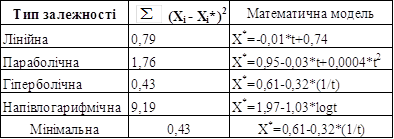
Результати розрахунків показників точності і адекватності між досліджуваними ознаками представлені в таблиці 3.19

Таблиця 3.19 – Розрахунок показників точності і адекватності

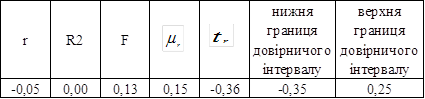
Отримані результати свідчать про те, що сума квадратів відхилень, отриманого значення X_i^* (апроксимуючого значення) від заданого значення X_i, мінімальна у випадку побудови гіперболічного поліному. Таким чином, найбільш точним поліномом є гіпербола, яка має таку математичну модель: X^*= 0,61-0,32*(1/t).

Розрахунок коефіцієнта кореляції говорить о том, що між досліджуваними ознаками зовсім немає зв’язку.

3.2.5 Розробка математичної моделі динаміки зміни коефіцієнта захищеності дохідних активів власним капіталом

В якості вихідних даних обраний такий показник фінансової стійкості, як коефіцієнт захищеності дохідних активів власним капіталом, який сигналізує про захист дохідних активів (що чутливі до зміни процентних ставок) мобільним власним капіталом. Розрахунок цього показника представлен у додатку А.

На основі представленої методики у розділі 2.2 розробляються математичні моделі різних типів. Представимо таблицю 3.20 з порівняльною оцінкою отриманих моделей та оптимальною моделлю.

Результати розрахунків показників точності і адекватності між досліджуваними ознаками представлені в таблиці 3.21

Таблиця 3.20 – Порівняльна оцінка моделей динаміки зміни коефіцієнта захищеності дохідних активів власним капіталом

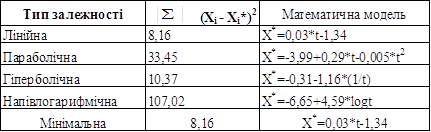
Таблиця 3.21 – Розрахунок показників точності і адекватності

Отримані результати свідчать про те, що сума квадратів відхилень, отриманого значення X_i^* (апроксимуючого значення) від заданого значення X_i, мінімальна у випадку побудови лінійного поліному. Таким чином, найбільш точним поліномом є лінія, яка має таку математичну модель: X^*=0,03*t-1,34.

Розрахунок коефіцієнта кореляції говорить о наявності прямого зв’язку між досліджуваними ознаками з середньою щільністю коефіцієнта захищеності дохідних активів власним капіталом від часу (0,67).

Отже, в обстеженій сукупності показників досліджуваного коефіцієнта у 44% варіації сигнал про захист дохідних активів мобільним власним капіталом пояснюється різним часовим періодом. Істотність зв’язку коефіцієнта детермінації R² перевірили за допомогою таблиці критерію F для 5%-ного рівня значущості. Критичне значення F_т(0,95)=5,32 значно менше від фактичного 5,32<36,69, що підтверджує істотність кореляційного зв’язку між досліджуваними ознаками.

При достатньо великому числі спостережень коефіцієнт кореляції можна вважати достовірним, тому що він перевищує свою помилку в більше ніж 3 рази, а отже зв’язок між коефіцієнтом достатності капіталу та часом доведений.

Двірничий інтервал: 0,50<r(0,67)<0,83.

Усе це дає підставу вважати, що обчислений лінійний коефіцієнт кореляції достатньо точно характеризує щільність зв’язку між досліджуваними ознаками.