Аналіз методів теорії синергетики

1.3 Аналіз методів теорії синергетики

У постнеокласичній картині світу упорядкованість, структурність, так само як і хаосомність, стохастичність, визнані об'єктивними, універсальними характеристиками дійсності. Вони виявляють себе на всіх структурних рівнях розвитку. Проблема іррегулярного поводження нерівноважних систем знаходиться в центрі уваги багатьох наукових дисциплін і насамперед синергетики - теорії самоорганізації, що зробила своїм предметом виявлення найбільш загальних закономірностей спонтанного структурогенеза.

Поняття синергетики одержало широке поширення в сучасних наукових дискусіях і дослідженнях останніх десятиліть в області науки і методології. Сам термін має давньогрецьке походження й означає сприяння, співучасть або сприяючий, допомагаючий. Сліди його вживання можна знайти ще в исихазмі – містичні течії Візантії.

1973 р.- рік виступу Г. Хакен на першій конференції, присвяченої проблемам самоорганізації, поклав початок новій дисципліні і вважається роком народження синергетики. М. Хакен звернув увагу на те, що корпоративні явища спостерігаються в найрізноманітніших системах . У своїй класичній роботі «Синергетика» він відзначав, що в багатьох дисциплінах, від астрофізики до соціології, ми часто спостерігаємо, як кооперація окремих частин системи приводить до утворення макроскопічних структур або функцій. Синергетика в її нинішньому стані фокусує увагу на таких ситуаціях, у яких структури або функції системи переживають драматичні зміни на рівні макромасштабу. Зокрема, синергетику особливо цікавить питання про те, як зміна підсистеми або її частини роблять зміни, цілком обумовлені процесами самоорганізації. Парадоксальним здавалося те, що при переході від неупорядкованого стану до стану порядку всі ці системи поводяться схожим образом [17].

« Я назвав нову дисципліну «синергетикою»,- писав у передмові до своєї книги «Синергетика», переведеної на багато мов, професор Штутгартського університету Г. Хакен,- не тільки тому, що в ній досліджується спільна дія багатьох елементів систем, але і тому, що для знаходження загальних принципів керуючих самоорганізацій, необхідне кооперування багатьох різних дисциплін». Відповідно до автора терміна, слово «Синергетика» має 2 смисли. З одного боку, мова йде про кооперативне сприяння елементів складних систем, а з іншого боку - про співробітництво учених різних областей знання [11].

У 1982 році на конференції по синергетиці були виділені конкретні пріоритети нової науки. Г. Хакен підкреслив, що в зв'язку з кризою узкоспеціалізованих областей знання інформацію необхідно зжати до невеликого числа законів, концепцій або ідей, а синергетику можна розглядати як одну з подібних спроб. На думку вченого, існують ті самі принципи самоорганізації різних по своїй природі систем, від електронів до людей, а значить мова повинна вестися про загальних детермінованих природних і соціальних процесів, на перебування яких і спрямована синергетика [17].

Так стало питання про те, як можна погодити висновок про зростання згодом ентропії в замкнутих системах (зростання невизначеності, хаосу) із процесами самоорганізації в живій і неживій природі, що відбуваються у відкритих системах [27]. Ентропія - показник необоротності. При будь-якому необоротному процесі ентропія зростає. Стримати ріст ентропії можуть тільки оборотні процеси [11].

По сучасних уявленням, у формуванні яких істотну роль зіграла кібернетика, процес самоорганізації являє собою автоматичний процес, при якому, якщо говорити про біологічні системи, виживають комбінації, вигідні з погляду адаптації усього виду й окремих організмів.

Кібернетика відіграє істотну роль у розумінні загальних принципів процесів самоорганізації і дає методи конструювання різних типів систем, що самоорганізуються. Однак при цьому залишається відкритим питання про фізичні процеси, що відбуваються в ході самоорганізації у всіляких системах. Ці процеси як правило дуже складні, але проте встановлення загальних закономірностей процесів самоорганізації виявляється можливим [27].

Структура (система) – це об'єкт, що володіє стійкістю, «жорсткістю». Структура має здатність до якоїсь межі «пручатися» зовнішнім і внутрішнім змінам, залишатися «вірної» собі, не змінюючись у цілому. Якщо ж такі зміни відбулися, то говорять про загибель, руйнування структури. Структури бувають 2 видів:

§    регулярні структури, наприклад, кристалічна решітка. Вони, як правило, складаються з однорідних елементів, розташованих симетрично;

§    нерегулярні - прикладом може бути будь-який живий організм, що складається з різнорідних кліток, розташованих за складним планом [11].

Згідно ідеї брюссельської школи, що істотно спирається на роботи Пригожина, відкритий характер гнітючої більшості систем у Всесвіті говорить про те, що реальність аж ніяк не є ареною, на якій панує порядок, стабільність і рівновага. Головну роль у навколишньому нас світі грають нестійкість і нерівноваженість [21].

В умовах, далеких від рівноваги, діють біфуркаційні механізми. Вони припускають наявність крапок роздвоєння і неодиничність продовження розвитку. Результати їхньої дії важко передбачувані. Біфуркаційні процеси свідчать про ускладнення системи. Флуктуації в загальному випадку означають обурення і підрозділяються на два великих класи:

·                клас флуктуацій, створюваних зовнішнім середовищем;

·                клас флуктуацій, відтворених самою системою [17].

Іноді окрема флуктуація або комбінація флуктуацій може стати (у результаті позитивного зворотного зв'язку) настільки сильною, що існуюча колись організація не витримує і руйнується. У цей переломний момент (називають особливою точкою або точкою біфуркації) принципово неможливо пророчити, у якому напрямку буде відбуватися подальший розвиток: чи стане стан системи хаотичним або вона перейде на новий, більш диференційований і більш високий рівень упорядкованості або організації, що називають дисипативною структурою. Фізичні або хімічні структури такого роду називають дисипативними тому, що для їхньої підтримки потрібно більше енергії, ніж для підтримки більш простих структур, на зміну яким вони приходять [21].

Таким чином, синергетика виявляється досить продуктивною науковою концепцією. Її предметом виступають процеси самоорганізації - спонтанного структурогенеза. Вона включила в себе нові пріоритети сучасної картини світу:

ª             концепцію нестабільного нерівноважного світу;

ª             феномен невизначеності і наявність великої кількості альтернатив розвитку;

ª             ідею виникнення порядку і хаосу.

Спроби осмислення понять порядку і хаосу, створення теорії спрямованого безладдя спираються на великі класифікації і типології хаосу. Останній може бути простим, складним, детермінованим і т.д. [17].

Інтуїтивно визначають хаос від противного: хаос панує там, де немає ніякого порядку, немає структури [11].

«...Порядок же має на увазі існування в навколишньому світі не тільки «законів», але і чогось ще: обмежень, інваріантостей, сталості якихось співвідношень, тієї або іншої регулярності...Стираючий усякі розходження, що знеособлює підхід старого детермінізму змінився всіляко підкреслюючи розходження еволюційним підходом, заснованим на використанні детермінацій» [21].

Найпростіший вид хаосу – «маломірний» - зустрічається в науці і техніку і піддається описові за допомогою детермінованих систем. Він відрізняється складним тимчасовим, але досить простим просторовою поведінкою. «Багатомірний» хаос супроводжує нерегулярне поводження нелінійних середовищ. У турбулентному режимі складними, що не піддаються координації будуть і тимчасові, і просторові параметри. Під поняттям «детермінований хаос» мають на увазі поведінку нелінійних систем, що описується рівняннями без стохастичних джерел, з регулярними початковими і граничними умовами.

Можна виділити ряд причин і обставин, у результаті яких відбувається втрата стійкості і перехід до хаосу:

§    шуми;

§    зовнішні перешкоди;

§    фактори, що обурюють.

Джерело хаосомности іноді зв'язують з наявністю різноманіття ступенів волі, що може привести до реалізації абсолютно випадкових послідовностей. До обставин, що обумовлюють хаосогенность, відноситься принципова нестійкість руху, коли два близьких стани можуть породжувати різні траєкторії розвитку, чуйно реагуючи на стохастику зовнішніх впливів.

Сучасний рівень досліджень приводить до істотних доповнень традиційних поглядів на процеси хаотизаціі. У постнеокласичну картину світу хаос увійшов не як джерело деструкції, а як стан, похідний від первинної нестійкості матеріальних взаємодій, що може з'явитися причиною спонтанного структурогенеза. У світлі останніх теоретичних розробок хаос з'являється не просто як безформна маса, але і як понад складно організована послідовність, логіка якої становить значний інтерес. Учені впритул підійшли до розробки теорії спрямованого безладдя, визначаючи хаос як нерегулярний рух з неперіодично повторюваними, хитливими траєкторіями, де для кореляції просторових і тимчасових параметрів характерно випадковий розподіл [17].

Процеси, що вивчаються в синергетиці, описуються нелінійними рівняннями. Макроскопічна система складається з величезної кількості взаємодіючих між собою частинок (електронів і ядер). Взаємодія між частинками відбувається через поля, і тому для визначення стану системи потрібно розв’язати систему рівнянь, що описують динаміку частинок і рівняння для полів (електромагнітних, гравітаційних та інших). Для макроскопічної системи, що складається з 10²³ частинок, виконати таку задачу неможливо. Крім того, у більшості випадків розв’язок такої задачі навіть непотрібний, оскільки при експериментальному визначенні величин, що характеризують систему, проводиться усереднення з величезною кількістю частинок. Тому для характеристики стану системи вводять макроскопічні параметри, значення яких формується різноманітними процесами, що відбуваються на макроскопічному рівні. Основні рівняння для макроскопічних змінних одержують різними шляхами:

§    з мікроскопічних рівнянь після усереднення по мікроскопічних змінних і нехтування неістотними для даного явища процесами;

§    з феноменологічних міркувань, постулюючи співвідношення між величинами;

§    одержуючи їх із законів збереження і вводячи параметри, значення яких отримуємо з досліду.

У загальному випадку ці рівняння є нелінійними і описують процеси нестійкості та явища самоорганізації в нерівноважних системах. Проте опис системи, що складається з величезної кількості частинок, обмеженим числом змінних є наближення. Вийти за рамки цього наближення можна, враховуючи флуктуації. Макроскопічні параметри, що визначають стан системи, називають динамічними змінними.

Отже, стан системи описується набором N динамічних змінних, які визначаються з основних законів досліджуваної області явищ. Позначимо i-ту динамічну змінну в момент часу t через X_i(t), де (i=1,2,..., N).Величина X_i(t) задовольняє системі диференційних рівнянь

 (1.15)

де i=1,2,...,N.

У цьому співвідношенні f_i(X₁, X₂,…X_N,,t) у загальному випадку – деяка нелінійна функція аргументів (вигляд функції визначається законами досліджуваної області). Величина  визначає сукупність параметрів, що описують внутрішні і зовнішні умови [24].

Важливою характеристикою розв’язків рівнянь є їх стійкість. Це зумовлено тим, що внаслідок дії різноманітних процесів, не врахованих у рівняннях (1.15), які часто мають випадковий характер, система може бути переведена з однієї фазової траєкторії в іншу.

Розглянемо деяку траєкторію X_i(t), яка є розв’язком системи (1.15). За теоремою Ляпунова розв’язок називається стійким, якщо для довільного моменту часу t для будь якого значення >0 можна знайти таке значення >0, що для будь-якого розв’язку , який задовольняє умові:

 (1.16)

має місце

 (1.17)

Розв’язок, який задовольняє умові

 (1.18)

при t називається асимптотично стійким.

Умови (1.16), (1.17) означають, що для стійкого руху фазові траєкторії не розбігаються. Умова (1.18) означає, що всі траєкторії асимптотично наближаються до однієї стійкої траєкторії [24].

Для систем з одним ступенем вільності вихідну систему рівнянь запишемо в одне рівняння першого порядку:

 (1.19)

Фазовим простором тут є пряма лінія. Особливі точки визначаються так:

 (1.20)

Приклад нелінійної функції і положення особливих точок для системи з однією динамічною змінною наведено на рис.1.2.

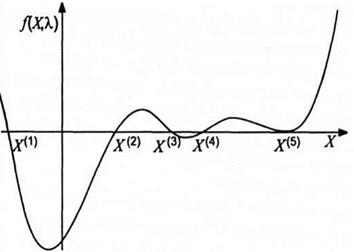
Рисунок 1.2- Особливі точки для системи з однією змінною

Згідно з теоремою Ляпунова для даного випадку розв’язок є стійким, якщо  (точки Х⁽¹⁾ і Х⁽³⁾ на рис. 1.2), і нестійким, якщо  (точки Х⁽²⁾ і Х⁽⁴⁾ на рис. 1.2). В точці Х⁽⁵⁾, у цьому разі питання про стійкість потребує окремого дослідження [24].

Проаналізуємо залежність розв’язку від зовнішнього параметра . Якщо зі зміною параметра функція  змінює знак, то змінюється також характер стійкості розв’язку поблизу особливої точки : стійка точка може стати нестійкою, і навпаки. Розглянемо на площині (Х, ) криву , яка описує положення особливої точки від параметра (рис. 1.3).

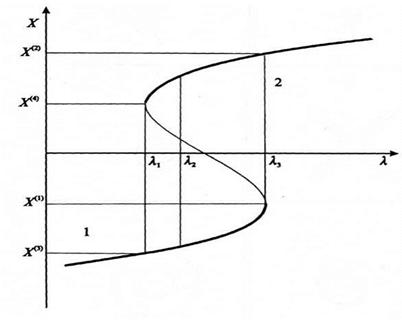
Рисунок 1.3 - Залежність положення особливої точки від зовнішнього параметра

Переріз кривої прямою =const визначає число і положення особливих точок при заданому значенні параметра .Характер стійкості визначається значенням похідної . З рисунка 1.3 випливає, що в області 1(), а в області 2 (). Тому можна визначити знак приросту функції зі зміною Х (тобто похідної) в області , а також характер стійкості. В області жирної лінії на рисунку 1.3 особливі точки стійкі, а в області тонкої - нестійкі. З рисунка 1.3 видно, що в областях і існує одна особлива точка, в області  система має три особливі точки: дві стійкі і одна нестійка. Зі зміною параметра  в точках і  відбувається різка зміна стану системи. Так, зі збільшенням параметра  від значень  стаціонарна точка рухається вдовж нижньої кривої. При досягненні точки  система стає нестійкою і з подальшим збільшенням  стаціонарна точка, що характеризує стан системи, стрибкоподібно переходить на верхню криву. Отже, з плавною зміною  раптово змінюється положення стійкої стаціонарної точки (від Х⁽¹⁾ до Х⁽²⁾). Аналогічно зі зміщенням при  точка рухається вдовж верхньої кривої (рисунок 1.3) і при  відбувається різка зміна стану системи від значення Х⁽⁴⁾ до Х⁽³⁾. Значення параметра , за яким різко змінюється число і характер особливих точок, називається біфуркаційним. Для прикладу, наведеному на рисунку 1.3, біфуркаційними є значення параметрів  і .

Також синергетика вивчає системи з двома ступенями вільності. Чисельні задачі такого рівня зводяться до вивчення зв’язків системи двох рівнянь з двома невідомими [24].

Серед розв’язків динамічних рівнянь особливе місце займають розв’язки, які описують періодичну зміну динамічного стану системи. На фазовій площині такому руху відповідає замкнена траєкторія. Ізольована замкнена траєкторія на фазовій площині називається граничним циклом. Якщо сусідні траєкторії при t наближаються до граничного циклу, то граничний цикл називається орбітально стійким (рис. 1.4а). У разі віддалення траєкторії від граничного циклу, то такий цикл називається орбітально нестійким (рис. 1.4б). Якщо траєкторія при t з одного боку наближається до граничного циклу, а з іншого віддаляється, то граничний цикл називається напівстійким (рис. 1.4в).

Наявність у системі граничного циклу свідчить про існування періодичних коливань, частота і амплітуда яких не залежать від початкових умов. Андронов назвав їх автоколиваннями. Автоколивання виникають за наявності позитивного зворотного зв’язку в системі, а їхня частота визначається внутрішніми параметрами системи. Рівняння, що описують автоколивання, є нелінійними. Автоколивання виникають в різноманітних явищах [24].

Рисунок 1.4 – Фазові траєкторії граничних циклів: а - стабільного,б - нестабільного, в – напівстабільного.