Навигация
Определение статических нагрузок в пружине и шарнирах
4 Определение статических нагрузок в пружине и шарнирах
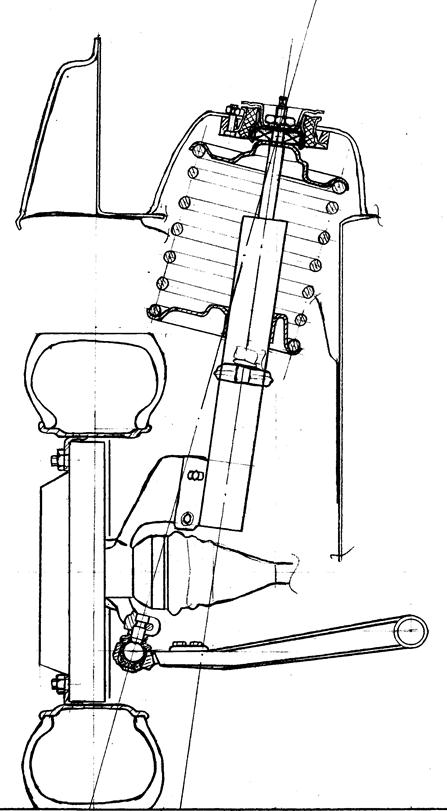
Рис. 4. Принятая расчетная схема подвески.
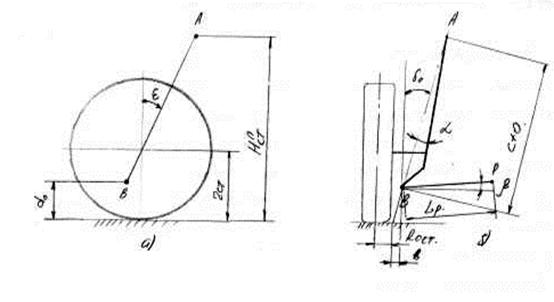
Рис. 4.1 Схема обозначения основных размерных параметров
(а) – вид сбоку (б) – вид сзади
В качестве расчетной принят тип подвески изображенный на рис. 4 со следующими конструктивные параметры подвески (рис. 4.1, а, б):
· Угол поперечного наклона оси поворота δo = 15º позволяет сместить несущий шарнир b в пространство колеса и получить отрицательное плечо обкатки, а также укоротить отрезок b.
· Угол продольного наклона оси поворота ε = 3º обеспечивает возврат управляемых колес в нейтральное положение при повороте. Значение последнего угла обеспечивает благоприятное расположение центра продольного крена и связанную с этим 20%-ную компенсацию продольного крена при торможении.
· Угол α = 7° смещения оси амортизатора относительно оси поворота также способствует созданию отрицательного плеча обкатки.
· Плечо обкатки Ro ст = -5 мм позволяет уменьшить плечо действия вертикальных нагрузок, тормозных и тяговых сил на амортизаторную стойку, улучшить динамику и кинематику подвески и ее компактность.
· Расстояние dо = 0,18 м (180 мм) от поверхности дороги до центра шаровой опоры колеса, принимается при статическом положении автомобиля и максимально допустимой нагрузке.
· Угол наклона поперечного рычага β = 3º35′ принимается с учетом, что в движении при незначительных колебаниях подвески автомобиля на ровной дороге он (автомобиль) будет занимать наиболее устойчивое положение при колее передних колёс 1314 мм.
· Высота подвески от поверхности дороги до точки крепления штока амортизатора в крыле автомобиля при номинальной нагрузке на ось принимается равной Нⁿст = 771 мм (без нагрузки Нⁿст = 800 мм.)
· Расстояние (с + о), характеризующее длину амортизаторной стойки при статическом номинальном нагружении автомобиля принимается равной 612 мм.
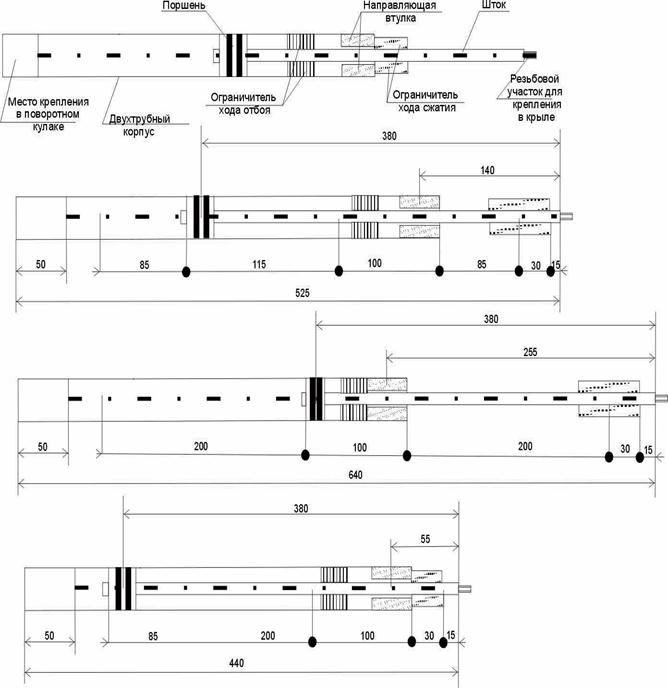
· Длина рычага ВД принимается равной Lр=325 мм, это позволяет уменьшить зависимость изменения развала от хода колеса при более коротких рычагах, а также добиться относительно большого хода подвески S = 150 мм (рис. 4.2).
|
| |||||||||||||||||||
|
| ||||||||||||||||||
|
| ||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
Силу F пружины определяют для неподвижного автомобиля, рассчитывая ее по законам статики.
Колесо, поворотная цапфа колеса, наружная труба амортизатора и шток при анализе статического равновесия образуют единое целое по отношению к точке А крепления на брызговике и нижнему рычагу, закрепленному в точке В (рис. 4.3).
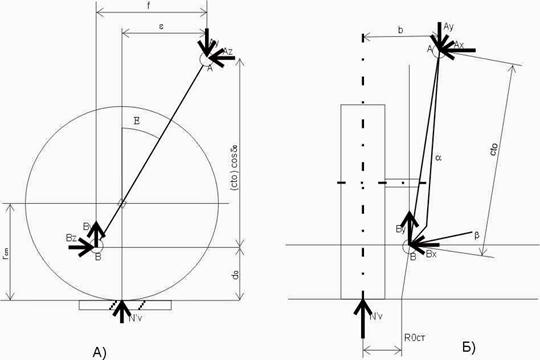
Рис.4.3 Виды подвески сбоку (а) и сзади (б), необходимые для определения сил, действующих в направлении оси Z.
Составляем уравнения моментов относительно оси Z и точки А.
Σ МОZА: NV ′ · b + Вy (c + o) sin δo – Bx (c + o) cos δo = 0;
где b = Ro ст + dotg δo + (c + o) sin δo;
Bx = By ctg β;
NV ′ (Ro ст + dotg δo + (c + o) sin δo + By (c + o) sin δo – – By (c + o) cos δo ctg β = 0;
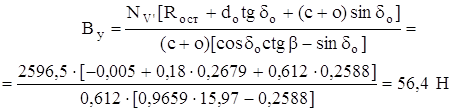
Bx = By ctg β = 56,4 · 15,97 = 900,71 Н
Сумма моментов относительно оси Х и точки А:
Σ МОХА : NV ′е + Вy t – BZ (c + o) cos δo = 0;
где t = (с + о) cos δo tg ε;
е = [(с + о) cos δo + dо – rст] tg ε.
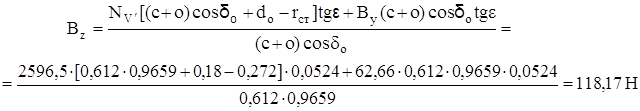
Āх + Вх = 0; Āy + Вy + NV′ = 0; Āz + Вz = 0;
Ах – Вх = 0; – Аy + Вy + NV′ = 0; Аz – Вz = 0;
Ах = Вх = 900,71 Н Аy = Вy + NV ′; Аz = Вz;
Аy = 56,4 +2596,5 = 2652,9 Н; Аz = 118,17 Н
Теперь необходимо эти силы разложить на составляющие в направлении линии оси амортизатора и перпендикулярно к ней.
Вертикальную силу Аy поэтому следует рассматривать отдельно и с учетом пространственного угла υ, разложить на составляющие в направлении осей U и V (рис. 5.2.). С учетом
tg υ = √tg² (δo – α) + tg² ε
tg υ = √tg² 8º + tg² 3° = √0,1405² + 0,0524² = 0,15
υ ≈ 8°32′.
получаем АYU = Аy sin υ = 2652,9 · 0,1484 = 393,69 Н
АYV = Аy cos υ = 2652,9 · 0,9889 = 2623,45 Н.
Силы Ах и Аz следует разложить и, учитывая угол æ на виде сверху системы сил на рис. 4.6, разложить на составляющие в направлении сил S и Т.
Поскольку
tg æ = tg (δo – α) / tg ε = 0,1405 / 0,0524 = 2,6813
æ = 69°33′.
Ахs = Ах · sin æ = 900,71 · 0,937 = 843,97 Н
Ахt = Ах · cos æ = 900,71 · 0,3494 = 314,71 Н
Аzs = Аz · cos æ = 118,17 · 0,3494 = 41,29 Н
Аzt = Аz · sin æ = 118,17 · 0,937 = 110,73 Н
Аs = Аzs + Ахs = 41,29 + 843,97 = 885,26 Н
Аt = Ахt – Аzt = 314,71–110,73 = 203,98 Н
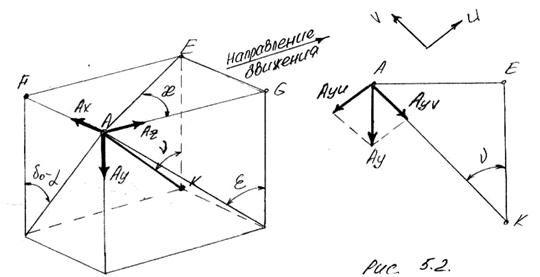
| Рис. 4.4 Пространственная система сил (ПСС) действующих в т. А крепления штока амортизатора в крыле автомобиля | Рис. 5.2. Вид пространственной системы сил на плоскость АЕК (ось амортизатора совпадает с линией АК). |
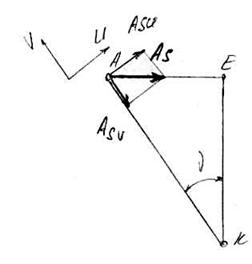
Силу Аs следует далее разложить на составляющие в направлениях U и V (рис. 4.7).
ASU = As cos υ = 885,26 · 0,9889 = 875,43 H
ASV = As sin υ = 885,26 · 0,1484 = 131,37 H.
Силы AYV и ASV совместно определяют нагрузку на пружину:
F1=AYV+ ASV =2623,45+131,37 =2754,82 Н.
Вторая составляющая ASU, также перпендикулярна к прямой АВ, как и AYU, приложена к штоку поршня. Чтобы иметь возможность определить напряжение изгиба, на основе двух сил с учетом силы Аt, действующей под углом 90° к ним, следует найти поперечную составляющую
AU = ASU – AYU = 875,43 – 393,69 = 481,74 Н.
Aguer = √Au² + At² = √481,74² + 20
3,98² = 523,15 Н .
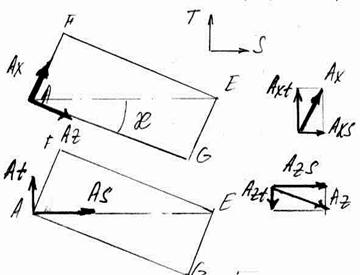
| Рис. 4.3. Видсверху на ПСС | Рис. 4.7 Разложение сил в направлении осей V и U |
Осуществляем проверку найденных сил:
√AX² + AY² + AZ² = √Fω² + AU² + At² ;
√900,71² + 2652,9² +118,17² = √2754,82² + 481,74² + 203,98² ;
2804,12 ≈ 2804,05.
Рис. 4.8 Силы изгибающие шток амортизатора | Изгибающий момент в штоке амортизатора: МК = Aguer · 0′ = 523,15 · 0,136 = 71,15 Нм. Сила в направляющей втулке штока амортизаторной стойки С= Сила, действующая на поршень, К = С - Aguer=860,35–523,15=337,2 Н. | |||||||||||||||||||||
На основе замеров характеристик упругости подвески с петлей гистерезиса сила трения, в данном случае, равная Сµ1 + Кµ2, является одной из демпфирующих сил и способствует повышению жесткости подвески.
5 Расчеты на прочность
5.1 Основные теоретические положения расчетов на прочность
При расчетах на прочность сопоставляют фактические и допустимые напряжения, чтобы гарантировать долговечность детали и убедиться в том, что даже при максимальных нагрузках не произойдет ее пластической деформации. Это может иметь место при условии, если будет превышено временное сопротивление или предел текучести материала. Во всех случаях уравнения для расчета будут иметь вид:σф = σдоп. и τ ф ≤ τ доп.
Фактически возникающие напряжения вызываются передаваемыми силами и моментами. Их величина зависит от размеров деталей, т. е. от внешних факторов. Допустимые напряжения зависят от тех характеристик материала, которые он будет иметь в данной детали, т. е. речь идет о возникающих в детали внутренних напряжениях.
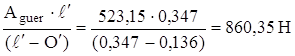 .
.
0 комментариев