Напряжения при изгибе

5.1.2. Напряжения при изгибе.

Верхнее и нижнее значения направлений изгиба

σ_bо = М_bo / W_b; σ_bu = М_bu / W_b.

При положительном значении σ_bu (и момента М_bu) имеет место знакопостоянная нагрузка, а при отрицательном – знакопеременная. В первом случае расчет ведется только по σ_bо и σ_bsch = 1,2 σ_s или 0,86 σ_b для σ_о . При знакопеременной нагрузке с учетом знаков на основе σ_bо и σ_bu следует определять соответственно среднее значение напряжений и амплитуду их изменения:

σ_bm = (σ_bо + σ_bu ) / 2; (1)

 σ_bа = σ_bо - σ_bm.  (2)

Обе эти величины необходимы для сопоставления с пределом выносливости материала при изгибе. При определении σ_bm следует не упустить из виду отрицательный знак перед σ_bu.

Через углы 50, 45 и 40° на диаграмме предельных напряжений (рис. 1.12 [1] ) можно получить расчетным путем величины допускаемых предельных напряжений при переменной нагрузке:

σ_bа + 0,159 σ_bm = σ_bw (3)

Коэффициент 0,159 получен из выражения, составленного для трех функций углов sin 5° / (sin 50° sin 45°). Целесообразно убедиться, что сумма амплитудного и среднего значений напряжений не превышает предела текучести при изгибе σ_bs:

 σ_bа + σ_bm ≤ σ_bs. (4)

При подстановке уравнений (1) и (2) в уравнение (3) можно непосредственно выразить σ_bw как функцию σ_bо и σ_bu :

 σ_{bw ф} = 0,58 σ_bо – 0,42 σ_bu. (5)

После того, как получено σ_{bw ф}, вновь действует условие σ_ф ≤ σ_{доп. D}, что в данном случае означает:

 σ_{доп. D} = σ_bw b₁ b₂ / (β_Nb β_Кb υ). (6)

Значение σ_bw, полученное из табл. 1.1. [1], должно быть равно σ_bw ≈ 0,5 σ_b или, в случае применения поверхностной закалки, σ_bw = 0,6 σ_b.

При поверочном расчете на статическую прочность следует определить запас прочности υ для предела текучести σ_bs при изгибе. Для этого следует лишь провести расчет в соответствии с уравнениями изгибающих моментов по большему из них:

 М_b2 (или М_b3) / W_b ≤ σ_bs / υ. (7)

Вводя σ_bs ≈ 1,2 σ_s (в случае применения поверхностного упрочнения умножая, кроме того, на коэффициент 1,2 ….. 1,5 в зависимости от глубины закаленного слоя), получаем:

υ ≥ 1,2 (или 1,44 ….. 1,8) σ_s ∙ 0,098 d³_min / М _b2 (или М_b3). Коэффициент должен быть по возможности близок к 1,5, но ни в коем случае не менее 1,2.

5.2 Расчет на выносливость и сопротивление усталости

Расчет на выносливость осуществляем для случая прямолинейного движения, а не при предельно допустимом сцеплении колес с дорогой при движении на повороте, так как при движении на повороте боковая сила на более нагруженное колесо направлена снаружи к центру поворота (т. е. она уменьшает момент N_оа (рис. 5.1). Кроме того, проведенные на дороге замеры показали, что на обычном легковом автомобиле боковые силы при прямолинейном движении вызывают более высокие усилия, чем при движении по кривой.

В последнем случае действует боковая сила, величина которой ограничена дорожным покрытием и шинами.

Несколько иная картина наблюдается в продольной плоскости, например, при резком торможении с начальной скоростью ниже V = 10 км/ч. На передних колесах имеет место очень сильное сцепление между широкими зонами контакта колес с дорогой благодаря низкой скорости автомобиля, в результате чего коэффициент сцепления в продольном направлении может достигать µ_L = 1,25.

Поэтому все детали оси должны быть дополнительно проверены расчетом, исходя из того, что может возникнуть продольная сила

L_BV = µ_L N_V = 1,25 N_V.

При разгоне, напротив, происходит увеличение нагрузки на заднюю подвеску и уменьшение на переднюю. Вместе с верхним значением вертикальной силы следует включить в расчет тяговое усилие

L_AV = µ_L N_V при µ_L = 0,8

В качестве условий трогание с места при заблокированных тормозах не рассматривается.

5.2.1 Определение верхних значений сил длительного действия

При расчете долговечности следует исходить из допустимой нагрузки на мост. Ниже приведены допустимые нагрузки, силы и веса деталей, а также плечи действия сил и углы:

Нагрузка на передний мост G_V = 5770 Н

Нагрузка на колеса N_V = 2885 Н

Половина веса неподрессоренных частей U_V /2 = 343,35 Н

Сила тяги на третьей передаче L_А1 = 352,8 Н

Плечо обкатки R_o = – 7 мм; R_{o ст} = – 5 мм

Угол наклона оси поворота в поперечной плоскости δ_о = 15°

Угол продольного наклона оси поворота колеса ε = 3°

Схождение и развал колес γ_о = 0°

Расстояние между точками А и В в направлении оси с+о= 612 мм=0,612 м

Высота точки над поверхностью дороги d = 203мм, d_о = 180 мм

Угол наклона рычага β β = 3°35′

Шины:

наружный диаметр D=588мм (544 c нагруз.)

статический радиус r_ст = 272 мм

диаметрический радиус r_д = 282 мм

Так как рассматриваемый автомобиль имеет продольный угол наклона колеса и является переднеприводным, в направляющем устройстве передней подвески возникают дополнительные силы, действующие в продольном направлении.

Действующую в пятне катящегося колеса силу тяги L_A1, следует вначале перенести в центр колеса, обозначив ее L′_A1, а затем как L′′_A1 перенести ее на ось поворота под прямым углом к последней. Это необходимо для расчета составляющих сил в направлении оси Z в точках А и В. Таким образом, сила тяги обозначаемая L_A1, оказывается смещенной от центра колеса вниз на величину а_L (рис. 5.1.).

а_L = R_o sin δ_o+ r_д sin (δ_o + γ _o) sin δ_o.

а_L = – 0,007 · 0,2588 +0,282 · 0,2588² = =0,01701 м.

Дополнительно следует перенести боковую силу S₁, которую следует рассматривать действующей на ось поворота колеса над дорогой на высоте:

n_s = r_д sin² ε = 0,282 · 0,0523² = 0,00077 м.

Вертикальные направляющие сил, которые необходимы для определения , можно получить, используя приведенный на рисунке вид сзади, по зависимости В_хо = В_уо сtg β и с помощью уравнения моментов относительно точки А:

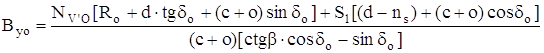
где N_V ′_О = К₁ N_V - U_V /2 = 1,6 · 2885 – 288,5 =4327,5 Н≈4,33 кН.

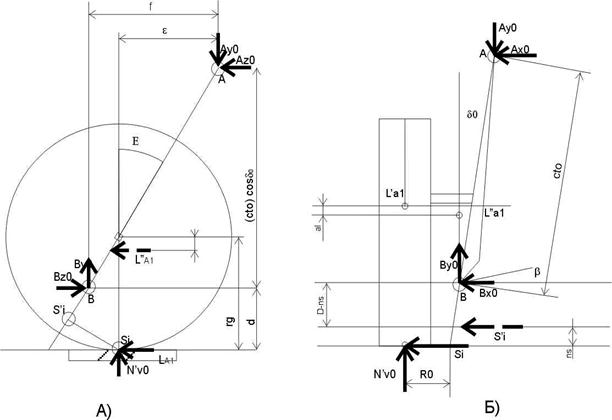 Рис. 5.1. Виды подвески сбоку (а) и сзади (б).

В_хо =В_уо∙ctgβ=179,78 · 15,97 =2871,09 Н.

Направление действия силы А_zо, приведенной на виде сбоку, не очевидно. Поэтому, составляя уравнение моментов относительно точки А, вначале определяем:

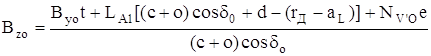
где t = (с + о) cos δ_o tg ε = 0,612∙0,9659∙0,0524 = 0,031 ;

 е = [(c + o) cos δ_o + d – r_д] tg ε = [0,612∙0,9659+0,203–0,282]∙0,0524 = 0,0268.

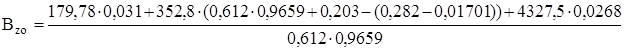
B_zo=521,43 Н.

В точке А действуют взаимно перпендикулярные силы:

- А_хо + В_хо - S₁ = 0; А_уо = В_уо + N_V ′_O; А_zо = В_zо - L_A1

А_хо = В_хо - S_1; А_уо = 179,78+4327,5; А_zо = 521,43–352,8

А_хо = 2871,09 –981= 1890,09 Н А_уо = 4507,28 Н А_zо =168,63 Н.

Эти силы раскладываем в направлении оси амортизатора и перпендикулярно ей аналогично статическому положению.

А_уu = A_yo · sin υ = 4507,28 · 0,1484 = 668,88 Н.

A_yv = A_yo · cos υ = 4507,28 · 0,9889 = 4457,25 Н.

A_xs = A_xo · sin æ = 1890,09 · 0,937 = 1771,01 Н.

A_xt = A_xo · cos æ = 1890,09 · 0,3494 = 660,4 Н.

A_zs = A_zo · cos æ = 168,63 · 0,3494 = 58,92 Н.

A_zt = A_zo · sin æ = 168,63 · 0,937 = 158,01 Н.

A_s = A_zs + A_xs = 58,92 + 1771,01 = 1829,93 Н.

A_tв = A_xt – A_zt = 660,4 – 158,01 = 502,39 Н.

A_su = A_s · cos υ = 1829,93 · 0,9889 = 1809,62 Н.

A_sv = A_s · sin υ = 1829,93 · 0,1484 = 271,56 Н.

F₁ = A_yv + A_sv = 4457,25 + 271,56 = 4727,81 Н.

A_uв = A_su – A_yu = 1809,62 – 668,88 = 1140,74 Н.

A_quer = √A_u² + A_t² = √1140,74² + 502,39² = 1246,47 Н.

Осуществляем проверку разложения сил на составляющие:

√А_хо² + А_уо² + А_zo² = √A_u² + A_t² + F₁² ;

√1890,09² + 4507,28² + 168,63² = √1140,74² + 502,39² + 4727,81² ;

4890,44 ≈ 4889,36

Следует дополнительно произвести расчет с использованием нижних значений нагрузки (знакопеременный или знакопостоянный), а также создание предпосылок для сложения всех сил, действующих в одной точке.