Преобразование знакопеременной нагрузки

5.2.5 Преобразование знакопеременной нагрузки

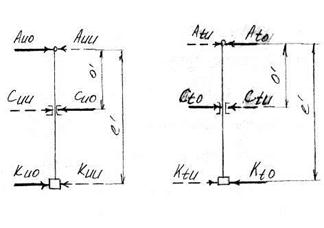
Рис. 5.4. Схема знакопеременных нагрузок действующих на шток и поршень

Определяем приведенные силы при знакопеременной нагрузке в направлениях U и Т (рис. 5.4).

А_uw = 0,58 А_uо + 0,42 А_uu = 0,58∙1140,74+0,42∙166,67 = 731,63 Н.

А_tw = 0,58 А_to + 0,42 А_tu= 0,58 · 502,39 + 0,42 · 18,04 = 298,96 Н.

В формуле учтены отрицательные значения коэффициента 0,42 и противоположно направленных сил.

Результирующая знакопеременных нагрузок:

А_w = √А_uw² + А_tw² = √731,63² + 298,96² = 790,35 Н

Момент, изгибающий шток:

М_лw = А_w · о′ = 790,35 · 0,136 = 107,49 Н∙м

В завершение следует определить минимальный для данного случая диаметр штока и убедиться, что имеющиеся напряжения не превышают допустимые.

В качестве материала штока применяем среднеуглеродистую, качественную сталь 40, обладающей следующими свойствами: σ_{b min}=568,98 Мпа, ε_s = 333,54 Мпа, δ_s=19% . Выбранная сталь дает отличные результаты при высокочастотной закалке, что для штоков амортизаторов весьма важно.

Допустимые напряжения:

σ_b = 0,6 σ_{b min} b₁ b₂ / (β_Кb · υ)=0,6 · 568,98 · 0,94 · 0,95 / (1 · 1,2) = 254,05 Мпа.

где 0,6 – коэффициент, справедливый для поверхностного упрочнения и вводится при использовании твердого хромирования штока амортизатора;

b₁ = 0,94 – масштабный коэффициент, отражающий снижение предела выносливости с увеличением диаметра; определен для Ø 20 мм;

b₂ – коэффициент, учитывающий шероховатость поверхности, обусловленную технологией обработки. При σ_{b min} = 700 МПа и высоте микронеровностей поверхности штока R_t = 6 мкм b₂ = 0,95;

β_Кb = 1 – коэффициент концентрации напряжений;

υ = 1,2 – коэффициент запаса прочности, обусловленный способностью поверхностного слоя при его упрочнении выдерживать в течение длительного времени возросшие примерно на 20% напряжения.

σ_b =

Чтобы иметь шток, упрочненный закалкой ТВЧ на 3 мм, принимаем минимальный его диаметр d_min = 20 мм.

Фактические напряжения от изгиба:

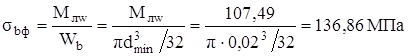
σ_{b ф} =136,86< σ_b=254,05

Условие усталостной прочности выполнено.

5.2.6 Определение сил, действующих на резиновые

шарниры рычага

Благодаря тому, что рычаг не воспринимает действие пружины, действующие на него и шарниры силы можно рассмотреть в плоскости.

 1. Определение верхних значений сил, действующих на резиновые шарниры.

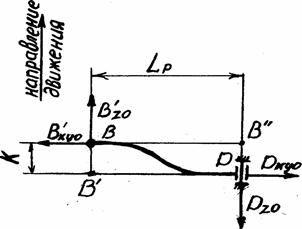
При расчете рычага приняты следующие размеры (рис. 5.5 ): L_р = 325 мм; к = 120 мм.

Сумма моментов относительно точки D:

ΣМ_D: В′_хуо ∙ к – В′_zо L_р= 0;

Рис. 5.5 Схема для определения верхних значений сил действующих на рычаг и резиновый шарнир.

│В′хуо│= Вхуо = √ Вхо² + Вуо² = =√2871,09²+ 179,78² =2876,71 Н; │В′zо│= Вzо = 521,43 Н. ∑МB’=В’хуо∙к–Dzo∙Lp=0

;

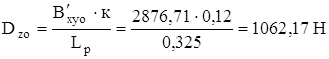∑M_B”=-B’_zo∙L_p+D_xyo∙к=0

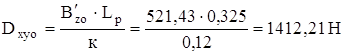
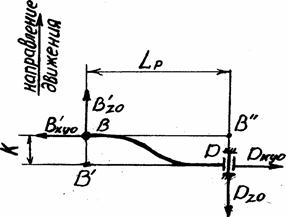
2 Определение нижних сил, действующих на резиновые шарниры

u   u   Рис. 5.6 Схема для определения нижних значений сил действующих на рычаг и резиновый шарнир.

│В′xуu │= Вxу u = √ Вx u ² + Ву u ² = = √(- 1032,62)² + (- 64,66)² = 1034,62Н; │В′z u │= Вzu = 352,8 Н. ΣМВ´ = В′ху u ∙ к – Dzo ∙ Lp = 0;

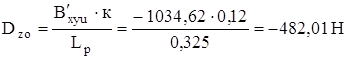
ΣM_B” =-В′_zu∙L_p+D_xyo∙к= 0;

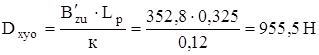
Расчет резинового шарнира будем производить по максимальной длительно действующей нагрузке в нем, т. е. при радиальной силе р = D_хуо = =1412,21 Н.