Классы моделей
Способы построения моделей
Особенности структурных моделей систем управления
Построение временных характеристик
Построение частотных характеристик
Построение моделей вход-выход по уравнениям в форме пространства состояний
Типовые звенья автоматических систем управления
Характеристики систем с типовой структурой
Неопределенность моделей систем управления
Динамические нелинейные элементы
Навигация
Классы моделей
Математическое моделирование и расчет систем управления техническими объектами
68359
знаков
14
таблиц
22
изображения
1.2 Классы моделей
Модель объекта или системы управления принадлежит тому же классу, что и описывающий их оператор преобразования. Выделяют следующие признаки классов систем с непрерывным и дискретным временем:
• линейные Л или нелинейные Л;
• стационарные С или нестационарные С;
• детерминированные Д или стохастичные Д;
• сосредоточенные (конечномерные) К или распределенные (бесконечномерные) К.
Эти четыре независимых признака биальтернативны, поэтому можно насчитать всего 24 = 16 классов непрерывных и столько же дискретных систем.
Простейший класс – ЛСДК – линейные стационарные детерминированные конечномерные системы. Они имеют форму обыкновенных линейных дифференциальных (разностных) уравнений с постоянными детерминированными коэффициентами. Математика разработала весьма развитый аппарат анализа этого класса систем.
Более сложные классы операторов получаются при введении одного из альтернативных признаков:
ЛСДК; ЛСДК; ЛСДК; ЛСДК.
Для таких систем существует незначительное число общих методов аналитического исследования, разработанных только для частных случаев. Операторы второго уровня сложности получаются введением двух отрицаний:
ЛСДК; ЛСДК; ЛСДК; ЛСДК; ЛСДК; ЛСДК.
При трех отрицаниях получаем операторы третьего уровня сложности:
ЛСДК; ЛСДК; ЛСДК; ЛСДК.
Операторы четвертого уровня сложности – ЛСДК – нелинейные нестационарные стохастичные бесконечномерные. Им соответствуют нелинейные дифференциальные уравнения в частных производных с переменными случайными параметрами.
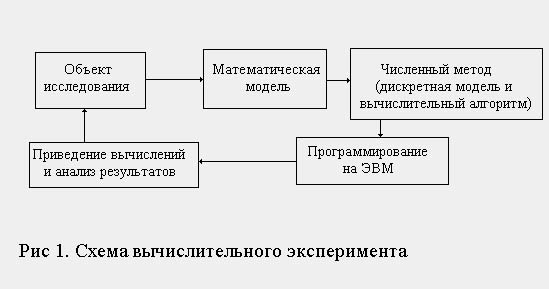
Для систем, описываемых операторами второго и выше уровней сложности, имеется, как правило, только единственная возможность их анализа и синтеза путем вычислительных экспериментов.
Если модель системы образована элементами различных классов, то класс системы определяется классом элемента с максимальным числом отрицаний.
Система называется автономной, если на нее не действуют внешние силы, в том числе параметрического типа. Автономные системы, таким образом, стационарны. Изменение их состояния происходит в силу накопленной ранее энергии. На рис.2 модель среды представлена в виде автономной системы, имеющей выходы, но не имеющей входов. Движения автономной системы называют свободными.
Дифференциальные уравнения автономных систем включают переменные системы и их производные, но не содержат переменных, описывающих воздействия среды, и имеют постоянные параметры. Это так называемые однородные дифференциальные уравнения
| ||||||||||||||||||||||||||||||||||
,
дополняемые начальными условиями 
Начальные условия являются следствием предыстории системы и вместе с дифференциальными уравнениями полностью определяют поведение автономной системы. В случае автономных систем с дискретным временем будем иметь однородные разностные уравнения:
.
Среда на входе системы моделируется автономными системами – генераторами воздействий или преобразователями типовых воздействий – фильтрами. Распространенными типовыми сигналами, моделирующими детерминированное воздействие, являются единичные импульсная и ступенчатая функции. Примером типового случайного воздействия является так называемый «белый шум». Среда может моделироваться динамической системой того же класса, что и сама система управления. Однако часто рассматриваются детерминированные системы со случайными воздействиями на входе.
Похожие работы
... балансовой, матричной моделью, причем выделяют как статические, так и динамические модели межотраслевого баланса[12]. 2. Основные направления применения методов и моделей исследования систем управления в современной экономике Производственная функция одной переменной Y = f(x) — функция, независимая переменная которой принимает значения объемов затрачиваемого ресурса (фактора производства), ...
... экспертов-консультантов - растет тенденциозность и безответственность Информационные : конференции улучшение информационной системы руководства практика открытых дверей Лекция 8 27.03.97 Методы исследования систем управления. План. Классификация методов в соответствии с решаемыми задачами. Учет закономерностей функционирования и развития систем при выборе методов их анализа. Краткая ...
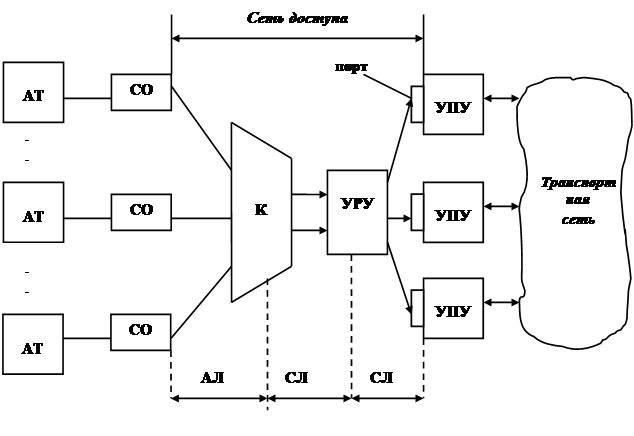
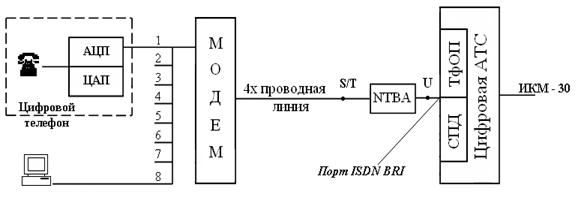
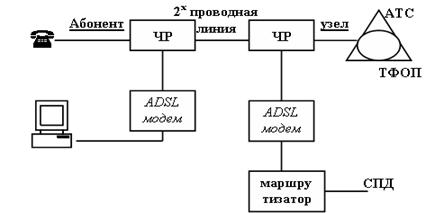
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
0 комментариев