Классы моделей
Способы построения моделей
Особенности структурных моделей систем управления
Построение временных характеристик
Построение частотных характеристик
Построение моделей вход-выход по уравнениям в форме пространства состояний
Типовые звенья автоматических систем управления
Характеристики систем с типовой структурой
Неопределенность моделей систем управления
Динамические нелинейные элементы
Навигация
Характеристики систем с типовой структурой
Математическое моделирование и расчет систем управления техническими объектами
68359
знаков
14
таблиц
22
изображения
2.8 Характеристики систем с типовой структурой
Системы с типовой структурой образуются последовательным (рис.18, a), параллельным (рис.18, б) соединениями звеньев или соединением с обратной связью (рис.18, в). Выявление свойств типовых систем в целом связано с построением эквивалентных систем со свернутой структурой (рис.18, г). Эквивалентные системы в терминах вход-выход могут быть представлены в форме дифференциального уравнения
Aэ(р)у(t) = Вэ(р)f(t), (65)
передаточная функция
временная характеристика:
|
|
;
частотная характеристика
Дифференциальные уравнения системы, образованной последовательным соединением звеньев, запишутся так:
A1(p)x1(t) = B1(p)f(t);
A2(p)x2(t) = B2(p)x1(t);
y(t) = x2(t).
В результате исключения переменных х1 и х2 получим операторные полиномы уравнения (65):
Аэ(р) = А1(р)А2(р); Вэ(р) = В1(р)В2(р).
Одновременно получаем передаточную функцию эквивалентного звена:
Wэ(s) =
W1(s)W2(s). 
(66)
Временную характеристику – импульсную переходную функцию получаем обратным преобразованием Лапласа передаточной функции (66):
wэ(t) =
.
Амплитудная частотная характеристика равна произведению соответствующих характеристик последовательно соединенных звеньев:
Rэ(w) = R1(w)R2(w),
фазочастотная характеристика равна сумме
jэ (w) = j1(w) + j2(w),
ЛАЧХ системы получается в виде суммы
Lэ(w) = L1(w) + L2(w).
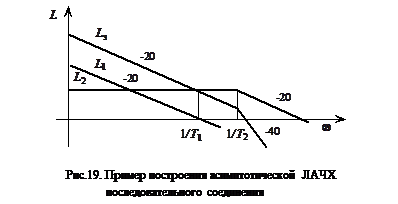
На рис.19 изображен пример графического построения ЛАЧХ системы, образованной последовательным соединением интегрирующего звена W1 и апериодического звена первого порядка W2.
Дифференциальные уравнения системы, образованной параллельным соединением звеньев (см. рис.18, б), запишутся так:
А1(p)x1(t) = В1(p)f);
А2(p)x2(t) = В2(p)f(t);
y(t) = x1(t) + x2(t).
|
|
В результате исключения переменных xi получим операторные полиномы эквивалентного уравнения (65):
Аэ(p) = А1(p)А2(р);
Вэ(p) = В1(p)А2(p) + А1(р)В2(р).
Передаточная функция эквивалентного звена получается как сумма передаточных функций звеньев:
Wэ(s) =
W1(s) + W2(s). (67)
Временная характеристика системы является суммой временных характеристик звеньев:
wэ(t) = w1(t)w2(t).
При параллельном соединении звеньев легко получить вещественную Рэ(w) и мнимую Qэ(w) частотные характеристики эквивалентного звена:
Рэ(w) = Р1(w) + Р2(w); Qэ(w) = Q1(w) + Q2(w).
Диполь передаточной функции Wэ(s) получается:
· если одна из передаточных функций звеньев имеет диполь;
· звенья имеют одинаковые полюсы А1(si) = A2(si) = 0.
Дифференциальные уравнения типового соединения с обратной связью:
А1(p)x1(t) = В1(p)x3(t);
А2(p)x2(t) = В2(p)x1(t);
x3(t) = f(t) 
x2(t);
y(t) = x1(t),
где знак «минус» соответствует отрицательной обратной связи, а знак «плюс» – положительной.
Исключение внутренних переменных дает операторные полиномы дифференциального уравнения эквивалентного звена:
Аэ(p) = А1(p)А2(р) B1(p)B2(р);
Вэ(p) = В1(p)А2(p). (68)
Передаточная функция эквивалентного звена:
Wэ(s) = 
. (69)
Если звенья образуют контур положительной обратной связи, то в формулах (69), (69) используется знак «минус».
Временная характеристика системы с обратной связью wэ(t) сложным образом зависит от w1(t) и wэ(t), поэтому ее удобнее получать обратным преобразованием Лапласа эквивалентной передаточной функции:
wэ(t) =
.
Комплексная частотная характеристика системы с обратной связью также сложным образом зависит от частотных характеристик звеньев:
Wэ(jw) = 
. (70)
Свойства системы с обратной связью определяются усилением разомкнутого контура с передаточной функцией Wp(s) = W1(s) + W2(s) на различных частотах. Если усиление контура мало, то можно пренебречь обратной связью. Действительно, по виду выражения (44) можно заключить, что на частотах, где выполняется условие
= 
<< 1
имеет место приближенное соотношение
Wэ(jw) » W1(jw).
Практически усиление контура считается малым, если
Lр(w) = 
< – (16-20) дБ.
С другой стороны, на частотах, где выполняется условие
>> 1,
имеет место другое приближенное соотношение
Wэ(jw) » 
.
Система в целом имеет частотную характеристику, близкую к обратной частотной характеристике звена обратной связи. Практически усиление велико, если Lр(w) > 16-20 дБ. На остальных частотах, где -16 дБ < LP(w) < 16 дБ, необходимо пользоваться точной формулой (70) или специальными номограммами замыкания.
Рассмотрим пример системы, образованной интегрирующим звеном, охваченным единичной отрицательной обратной связью (рис.20, а). На рис.20, б изображены ЛАЧХ L1 и L2 этих звеньев. На частотах w < 0,1 с-1 усиление контура превышает 20 дБ.
Следовательно, амплитудно-частотная характеристика замкнутой системы на этих частотах определяется только свойствами звена обратной связи, т.е. замкнутая система на низких частотах с большой степенью приближения ведет себя как безынерционное звено с единичным усилением.
Напротив, на частотах w > 10 с-1 усиление контура ниже –20 дБ. Здесь контур практически разомкнут – замкнутая система ведет себя как интегрирующее звено,
|
. | |
На комплексной частоте нуля передаточной
функции Wp усиление контура равно нулю, т.е. контур как бы разомкнут на соответствующей комплексной частоте. Если Wp имеет такой полюс, то в разложении Wp на сумму простейших дробей соответствующий коэффициент Сi равен нулю.
На рис.21 изображена структурная схема системы с единичной обратной связью, где звено в прямой цепи
W1(s) = Wp(s)
представлено как параллельное соединение простейших звеньев.
Похожие работы
... балансовой, матричной моделью, причем выделяют как статические, так и динамические модели межотраслевого баланса[12]. 2. Основные направления применения методов и моделей исследования систем управления в современной экономике Производственная функция одной переменной Y = f(x) — функция, независимая переменная которой принимает значения объемов затрачиваемого ресурса (фактора производства), ...
... экспертов-консультантов - растет тенденциозность и безответственность Информационные : конференции улучшение информационной системы руководства практика открытых дверей Лекция 8 27.03.97 Методы исследования систем управления. План. Классификация методов в соответствии с решаемыми задачами. Учет закономерностей функционирования и развития систем при выборе методов их анализа. Краткая ...
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
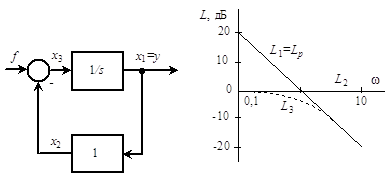
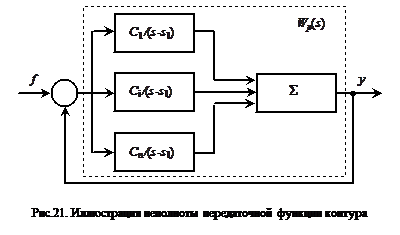
0 комментариев