Классы моделей
Способы построения моделей
Особенности структурных моделей систем управления
Построение временных характеристик
Построение частотных характеристик
Построение моделей вход-выход по уравнениям в форме пространства состояний
Типовые звенья автоматических систем управления
Характеристики систем с типовой структурой
Неопределенность моделей систем управления
Динамические нелинейные элементы
Навигация
Построение временных характеристик
Математическое моделирование и расчет систем управления техническими объектами
68359
знаков
14
таблиц
22
изображения
2.2 Построение временных характеристик
Временные характеристики – импульсная переходная функция w(t) и переходная характеристика h(t) могут быть получены экспериментально, если удается подать на вход объекта воздействие в виде достаточно узкого импульса с необходимой амплитудой или ступенчатой функцией времени. Последнее более реально – функцию веса w(t) впоследствии можно получать дифференцированием функции h(t).
Статистические методы непараметрической идентификации позволяют оценить ординаты функции веса w(t) путем обработки данных вход-выход объекта в виде случайных сигналов, возможных в режиме нормальной эксплуатации (корреляционный анализ).
Существуют методы построения временных характеристик по частотным, базирующиеся на обратном преобразовании Фурье. В случае, когда исходная информация об объекте представлена в форме дифференциального уравнения (1), временные характеристики получают его решением.
В классической теории автоматического управления для решения дифференциальных уравнений часто привлекают так называемый операторный метод, связанный с преобразованием Лапласа. Метод особенно удобен в случае типовых воздействий в виде обобщенных функций и позволяет легко учесть ненулевые начальные условия.
Пусть дано дифференциальное уравнение n-порядка звена или системы автоматического управления (2). Необходимо получить выражения для импульсной переходной функции (функции веса) w(t), переходной характеристики h(t), а также для реакции в случае воздействия общего вида. Пусть изображение по Лапласу воздействия на входе системы или звена представляет собой дробно-рациональную функцию от s:
.
Если преобразовать по Лапласу дифференциальное уравнение n-го порядка при ненулевых предначальных условиях, то после разрешения полученного алгебраического уравнения относительно изображения переменной выхода имеем
. (7)
Здесь полином AH(s) определяется предначальными условиями. Если все предначальные условия нулевые, то изображение выхода
где W(s) – передаточная функция.
Искомое решение – переменная на выходе системы (оригинал) получается обратным преобразованием Лапласа:
(8)
где с – абсцисса сходимости.
Формула обращения Римана – Меллина устанавливает однозначное соответствие между оригиналом и изображением в точках непрерывности оригинала. Имеются алгоритмы и программы, позволяющие вычислять интеграл (8) при произвольных функциях Y(s). Практическое вычисление оригинала у(t) удобно производить, основываясь на теореме о вычетах, согласно которой значение интеграла (8) может быть представлено суммой вычетов подынтегральной функции,
,
где ResY(s) – вычет функции Y(s) в полюсе si; i = 1,...,nY; nY – число полюсов изображения Y(s); при t < 0 функция у(t) = 0.
Для обыкновенных линейных дифференциальных уравнений и типовых воздействий изображение Y(s) является дробно-рациональной функцией, которую можно представить в виде суммы простейших дробей:
, (9)
где 
– производная полинома AY по s; si – простые полюсы;
Оригинал y(t) в соответствии с разложением (9) имеет вид:
.
Импульсная переходная функция (функция веса) w(t) представляет собой реакцию системы на 
-функцию при нулевых начальных условиях. Поскольку изображение -функции 
, то функция веса представляет собой обращение по Лапласу передаточной функции и
.
Разложение передаточной функции на сумму простейших дробей в случае простых полюсов si; i = 1, …, n имеет вид:
, (10)
где Ci – коэффициент разложения (вычета),
. (11)
Пример. Рассмотрим определение функции веса с помощью формул (10) и (11) для передаточной функции
. (12)
Полюсы передаточной функции s1 = -1; s2 = -2. Разложение (12) на сумму простейших дробей имеет вид:
.
Обратное преобразование Лапласа дает
.
Переходная характеристика h(t) представляет собой реакцию системы на единичную ступенчатую функцию I(t) при нулевых начальных условиях. Поскольку 
, то 
.
Полюсами изображения являются полюс воздействия s1 = 0 и полюсы передаточной функции. Легко убедится, что
, 
.
Пример. Рассмотрим получение переходной характеристики системы с передаточной функцией (12). Разложение изображения H(s) на сумму простейших дробей:
,
где
;
;
.
Следовательно, переходная характеристика описывается функцией
.
В общем случае произвольного воздействия разложение изображения переменной выхода (7) запишется так:
, (13)
где si, i = 1, …, n – полюсы передаточной функции W(s); sk, k = 1, …, nF – полюсы изображения воздействия F(s); принято, что 
, т. е. полюсы воздействия не равны полюсам передаточной функции (нет обобщенного резонанса).
В выражении (13) первая группа слагаемых определяет переходную составляющую вынужденного движения yпер(t); вторая группа – установившаяся составляющая вынужденного движения yуст(t), третья – свободные движения yсв(t):
.
Установившееся вынужденное движение yуст(t) обусловлено полюсами изображения воздействия sk; переходная составляющая вынужденного движения yпер(t) образуется из-за ненулевых посленачальных условий (изменение начальных условий приложением в момент времени t = 0 конкретного воздействия) и определяется полюсами передаточной функции; свободные движения yсв(t) имеют место при ненулевых предначальных условиях и также определяются полюсами передаточной функции.
Если анализируется автономная система автоматического управления Ms, представленная в форме однородного дифференциального уравнения
; y(0),
то его решение имеет вид:
. (14)
Если изображение Y(s) имеет кратные полюсы, то вместо формул (13), (14) записываются более сложные выражения.
Похожие работы
... балансовой, матричной моделью, причем выделяют как статические, так и динамические модели межотраслевого баланса[12]. 2. Основные направления применения методов и моделей исследования систем управления в современной экономике Производственная функция одной переменной Y = f(x) — функция, независимая переменная которой принимает значения объемов затрачиваемого ресурса (фактора производства), ...
... экспертов-консультантов - растет тенденциозность и безответственность Информационные : конференции улучшение информационной системы руководства практика открытых дверей Лекция 8 27.03.97 Методы исследования систем управления. План. Классификация методов в соответствии с решаемыми задачами. Учет закономерностей функционирования и развития систем при выборе методов их анализа. Краткая ...
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
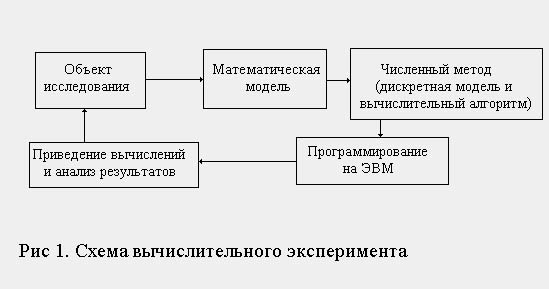
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
0 комментариев