Построение частотных характеристик

2.3 Построение частотных характеристик

Частотные характеристики (6) – амплитудную R() и фазовую  можно получать экспериментальным путем, если удается подавать на вход устойчивого объекта гармонические воздействия различных частот из диапазона существенного для выявления требуемых свойств объекта. Статистические методы непараметрической идентификации (спектральный анализ) позволяют оценить значения частотных характеристик путем обработки временных последовательностей на входе и выходе объекта.

Частотные характеристики можно получить по временным характеристикам с помощью преобразования Фурье.

В том случае, когда исходная информация об объекте представлена в форме дифференциального уравнения (1), частотные характеристики строят расчетным путем.

Рассмотрим переходы от дифференциального уравнения n-порядка (1) и передаточной функции (3) к частотным характеристикам.

Установившиеся реакции линейной системы на гармоническое воздействие единичной амплитудысоответствуют частному решению неоднородного дифференциального уравнения (2). Будем искать частное решение:

,

где R(w), j(w) – амплитуда и фаза, в общем случае зависящие от частоты.

Учтем, что

, ;

, .

Подставим эти соотношения в неоднородное дифференциальное уравнение (2), записанное в операторной форме,

.

После деления обеих частей на ехр{jwt} можно записать:

.

Таким образом, амплитудно-частотная характеристика находится как модуль

,

а фазовая частотная характеристика – как аргумент

j(w) = argW(jw)

комплексной частотной характеристики W(jw).

Одновременно получаем переход от передаточной функции к частотным характеристикам. Комплексная частотная характеристика получается заменой аргумента передаточной функции s на jw:

.

В общем случае s может принимать значения на любом контуре комплексной плоскости.

Вычисление значений частотных характеристик для конкретного s = jw (а в общем случае s = a + jw) сводится к вычислению значений полиномов В(s) и А(s) с последующим делением полученных комплексных чисел. При этом получаются значения вещественной P(w) и мнимой Q(w) частотных характеристик. Значение амплитудной частотной характеристики вычисляется как

.

Трудности возникают при расчете значений фазочастотной характеристики по формуле

; k = 0,  … (15)

Значения j(w) получаются на интервале (- p, p), поэтому в случае систем высокого порядка для определения истинных значений фазовых сдвигов принимается предположение о том, что в пределах выбранного шага частот j(w) не изменяется на ± p, т.е. корни полиномов B(s) и A(s) располагаются достаточно далеко от мнимой оси.

Соотношение (15) не определяет аргумент j(w) комплексного числа W(jw), так как ему вместе с j удовлетворяет и j + p. Однако из-за непрерывности фазовой характеристики j(w), принимающей отличные от нуля значения, она однозначно характеризуется текущим tgj(w) = Q(w)/P(w), w_min < w < w_max и начальным j(w₀); w_min < w < w_max значениями. На этом свойстве непрерывности фазовой характеристики можно получить алгоритм построения частотных характеристик, если истинное значение j(w₀) лежит в пределах (- p, p).

2.4 Построение моделей по системе дифференциальных уравнений

Системы дифференциальных уравнений обычно получаются в результате построения аналитическим методом математических моделей физических систем с сосредоточенными компонентами.

Пусть исходные знания об объекте управления имеют вид некоторой физической системы с сосредоточенными компонентами; это может быть, например, многоконтурная электрическая или механическая схема. На основе соответствующих законов по определенным правилам записываются компонентные уравнения и уравнения связей. Далее эти уравнения можно привести к следующему виду:

 i = 1, …, N;(16)

 q = 1, …, K.

Уравнения (16) можно записать в матричном виде:

A(p)x(t) = B(p)f(t);

y(t) = C(p)x(t),

где х – вектор внутренних переменных размерности N; f и y – векторы переменных входа и выхода размерностей Р и K соответственно; А(р), В(р), С(p) – полиномиальные матрицы; обычно матрица С – числовая, т. е. состоит из нулей и единиц, указывающих, какие из переменных х принимаются за выходные.

Уравнения (16), (17) называют непричинно-следственными, между внутренними переменными x_i(t) нет объективных причинно-следственных отношений.

При определенных условиях систему (16) можно записать в форме системы дифференциальных уравнений первого порядка, разрешенных относительно производных,

 i = 1, …, n,

дополненной уравнениями выходов

y_q(t) =  q = 1, …, K.

Модели в терминах вход-состояние-выход используют понятие состояния. Состояние динамического объекта (с памятью) – необходимая и достаточная информация для определения будущего поведения по дифференциальным уравнениям при заданных входных воздействиях независимо от того, каким путем система пришла в это состояние. Для конечномерных систем состояние представляется как n-мерный вектор n(t); при t = 0 вектор n(0) – начальное состояние. Система дифференциальных уравнений первого порядка в так называемой нормальной форме пространства состояний (стандартизованной векторно-матричной форме) записывается следующим образом:

An + Bf, n(0);

(18)

y = Cn + Df,

где f – Р-мерный вектор входа; у – K-мерный вектор выхода; A – матрица состояний; B – матрица входа; C – матрица выхода; D – матрица обхода соответствующих размеров. Первую векторно-матричную строку в системе уравнений (18) называют уравнениями состояний, а вторую – уравнениями выхода.

Пример. При n = 2 дифференциальные уравнения (18) системы с одним входом и одним выходом в раскрытой форме запишутся так:

Матрицы будут иметь следующий вид:

A = ; B = ;

C = (c₁ c₂); D = d.

Если первое уравнение в системе (18) записать с использованием оператора дифференцирования р, то имеем: (pI – A)n = Bf, где I – единичная матрица. Таким образом, уравнения в форме пространства состояний являются частным случаем системы дифференциальных уравнений (17) с матрицей

A(p) = pI – A. (19)

Автономная система описывается однородным дифференциальным уравнением

; ,

причем начальные условия являются математическим отражением предыстории. Если они ненулевые, то система совершает так называемые свободные движения. В конечномерных системах свободные движения определяются полностью оператором А(р) и конечным числом начальных условий независимо от того, каким путем система пришла в это состояние к моменту начала наблюдения.

Автономная система может описываться системой дифференциальных уравнений различных порядков:

A(p)x(t) = 0, x(0);

y(t) = Cx(t),

а также дифференциальными уравнениями в форме пространства состояний

 = An, n(0);

y = Cn.

Рассмотрим построение моделей вход-выход по системе дифференциальных уравнений. Пусть дана система дифференциальных уравнений (17). Построение модели в терминах «вход-выход» означает исключение внутренних переменных, что проще выполнить, если от дифференциальных уравнений перейти к системе алгебраических уравнений для изображений, приняв нулевые начальные условия:

A(s)X(s) = B(s)F(s); (20)

Y(s) = CX(s).

При небольшом числе уравнений применяют метод последовательных исключений. Пусть, например, объект с одним входом f и одним выходом у имеет две внутренние переменные x₁ и х₂:

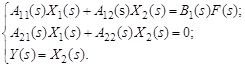 (21)

Решая систему (21) относительно Y(s), получим:

Теперь по выражению

легко получить полиномы числителя и знаменателя передаточной функции и записать выражение для одного дифференциального уравнения. Используем операции перемножения и вычитания полиномов.

В случае, когда требуется вычислить передаточную функцию, связывающую одну из выходных переменных у = x_q с одним из воздействий f_r, применяют правило Крамера:

, (22)

где полиномиальная матрица A_qr получена из матрицы А заменой q-го столбца r-м столбцом матрицы В. Знаменатель передаточной функции W_qr(s) независимо от номеров входа r и выхода q равен характеристическому полиному системы

A(s) = det A(s) (23)

Этот способ построения моделей вход-выход по системе уравнений (20) сводится к вычислению определителей полиномиальных матриц.

Для примера (21) запишем систему в матричной форме (20); матрицы имеют вид:

A(s) = ; B(s) = . (24)

В соответствии с правилом Крамера по формуле (23) определяем характеристический полином:

числитель передаточной функции W₂₁(s) (здесь r = 1, q = 2) равен

detA₂₁ =

Имеем систему алгебраических уравнений многомерной системы, записанную для изображений переменных (20). В общем случае передаточная матрица системы, т.е. модель вход-выход через полиномиальные матрицы выражается следующим образом:

W(s) = CA^-1(s)B(s). (25)

Здесь вычисления связаны с обращением и перемножением полиномиальных матриц. Ясно, что полиномиальная матрица системы А(s) должна быть не особенной, иными словами, ее определитель не равен тождественно нулю. Известно, что

,

где А^*(s) – присоединенная матрица.

Следовательно, выражение для передаточной матрицы (25) примет вид:

W(s) = CA^*(s)B(s)/A(s). (26)

Пример. Модель вход-выход в виде линейного дифференциального уравнения

y⁽ⁿ⁾ + a₁y^(n-1) + … + a_n-1y⁽¹⁾ + a_ny = b₀u⁽ⁿ⁾ + b₁u^(n-1) + … + b_nu

может быть приведена к модели в переменных состояния следующим образом:

x⁽¹⁾ = x_{i + 1} + k_i^*u, где i = 1, n-1;

x⁽¹⁾_n = – a_nx₁ – a_n-1x₂ –…– a₁x_n + k_nu;

y = x₁ + k₀u;

коэффициенты k рассчитываются по рекуррентным формулам:

k₀ = b₀;

k₁ = b₁ – a₁k₀;

…

;

,

где n = 3; a₁ = 0; a₂ = 2; a₃ = 4; b₀ = 2; b₁ = b₂ = 0; b₃ = –1.

Определим значение k_i:

k₀ = b₀ = 2;

k₁ = b₁ – a₁^*k₀ = 0;

k₂ = b₂ – a₁k₁ – a₂k₀ = – 4;

k₃ = b₃ – a₁k₂ – a₂^*k₁ – a₃k₀ = – 9.

Тогда исходное уравнение в переменных состояниях (нормальная форма):

x₁⁽¹⁾ = x₂;

x₂⁽¹⁾ = x₃ – 4u;

x₃⁽¹⁾ = – 4x₁ – 2x₂ – 9u;

y = x₁ + 2u,

или в векторной форме

;

,

где матрицы объекта, управления, наблюдения и обхода, соответственно,

; ; ; .

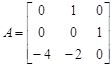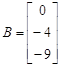Похожие работы

Научная полемика в исследовании систем управления

Скачать

38437

0

1

... балансовой, матричной моделью, причем выделяют как статические, так и динамические модели межотраслевого баланса[12].   2. Основные направления применения методов и моделей исследования систем управления в современной экономике Производственная функция одной переменной Y = f(x) — функция, независимая переменная которой принимает значения объемов затрачиваемого ресурса (фактора производства), ...

Исследование систем управления

Скачать

59152

14

0

... экспертов-консультантов - растет тенденциозность и безответственность Информационные : конференции улучшение информационной системы руководства практика открытых дверей Лекция 8 27.03.97 Методы исследования систем управления. План. Классификация методов в соответствии с решаемыми задачами. Учет закономерностей функционирования и развития систем при выборе методов их анализа. Краткая ...

Математическое моделирование услуг Интернет

Скачать

222848

26

34

... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...

Математическое моделирование как философская проблема

Скачать

50434

0

2

... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...