Навигация
Типовые звенья автоматических систем управления
2.7 Типовые звенья автоматических систем управления
При исследовании САУ ее разбивают на простые звенья. В результате этого математическое описание каждого звена может быть составлено без учета связей его с другими звеньями, а описание всей САУ получено как совокупность уравнений отдельных звеньев.
Уравнение усилительного звена имеет вид:
y = Kx. (36)
Передаточная функция в этом случае:
W(p) = K. (37)
Амплитудно-фазовая характеристика:
W(jw) = K. (38)
Примером усилительного звена является рычаг. Уравнение рычага имеет вид
![]()
Уравнение апериодического звена имеет вид:
![]() . (39)
. (39)
Передаточная функция:
![]() (40)
(40)
Амплитудно-фазовая характеристика:
![]() (41)
(41)
АФЧХ представляет собой полуокружность с радиусом K/2 и центром в точке (K/2,j*0) на действительной оси (рис.10).
Логарифмическая амплитудная частотная характеристика
![]() (42)
(42)
При малых значениях w << 1/Т
![]() (43)
(43)
На больших частотах, когда w >> 1/T
![]() . (44)
. (44)
В соответствии с выражениями (43) и (44) на рис.10, б приведена ЛАЧХ апериодического звена. Примером апериодического звена является рассмотренная ранее емкость.
Уравнение колебательного звена:
![]() (45)
(45)
| |
причем Т1 и Т2 связаны условием
![]() (46)
(46)
Это условие означает, что корни характеристического уравнения вида
![]() (47)
(47)
соответствуют дифференциальному уравнению (45), являются комплексными. Передаточная функция, соответствующая уравнению (45), имеет вид
![]() (48)
(48)
Переходная функция, являющаяся решением уравнения (45) при х = l(t), приведена на рис.11.
Амплитудно-фазовая характеристика звена (рис.12):
![]() . (49)
. (49)
Примером колебательного звена являются электрический резонансный контур (рис.13)и двухъемкостная схема (рис.14).
Если в уравнении (45) выполняется условие
![]() , (50)
, (50)
то характеристическое уравнение (47) имеет отрицательные действительные корни. В этом случае звено называется апериодическим звеном второго порядка. Все рассмотренные выше звенья называются статическими.
Уравнение интегрирующего звена:
![]() (51)
(51)
или в интегральной форме:
![]() (52)
(52)
| |
Переходная функция интегрирующего звена имеет вид (рис.15, а):
![]() ; (53)
; (53)
передаточная функция:
![]() (54)
(54)
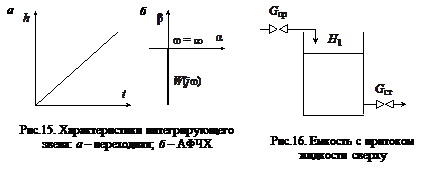
амплитудно-фазовая характеристика (рис.15, б):
![]() (55)
(55)
Иногда применяется другая форма записи уравнения интегрирующего звена:
![]() (56)
(56)
Примером интегрирующего звена является емкость с притоком жидкости сверху, причем расход на стоке не зависит от уровня в емкости (рис.16). Такая емкость не обладает самовыравниванием на притоке. Интегрирующее звено называется астатическим.
Уравнение дифференцирующего звена:
![]() (57)
(57)
переходная функция:
![]() ; (58)
; (58)
передаточная функция:
![]() ; (59)
; (59)
амплитудно-фазовая характеристика:
![]() , (60)
, (60)
| |
т.е. она совпадает с положительной мнимой полуосью.
Характеристики дифференцирующего звена обратны характеристикам интегрирующего звена. Идеальных дифференцирующих звеньев в природе не существует, но они используются при анализе сложных систем, из которых можно выделить дифференцирующие звенья.
Звено с запаздыванием без искажения воспроизводит на выходе входную величину, задерживая ее на время запаздывания t.
Уравнение такого звена имеет вид:
![]() ; (61)
; (61)
передаточная функция:
![]() ; (62)
; (62)
амплитудно-фазовая характеристика:
![]() . (63)
. (63)
Примерами таких звеньев являются транспортеры (рис.17), длинные трубопроводы и т.д. Если известны расстояние l и скорость движения ленты транспортера v, то запаздывание можно определить по формуле
![]() . (64)
. (64)
Похожие работы
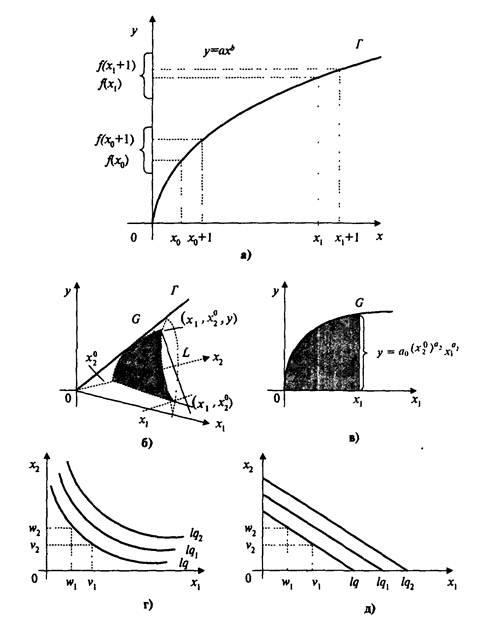
... балансовой, матричной моделью, причем выделяют как статические, так и динамические модели межотраслевого баланса[12]. 2. Основные направления применения методов и моделей исследования систем управления в современной экономике Производственная функция одной переменной Y = f(x) — функция, независимая переменная которой принимает значения объемов затрачиваемого ресурса (фактора производства), ...
... экспертов-консультантов - растет тенденциозность и безответственность Информационные : конференции улучшение информационной системы руководства практика открытых дверей Лекция 8 27.03.97 Методы исследования систем управления. План. Классификация методов в соответствии с решаемыми задачами. Учет закономерностей функционирования и развития систем при выборе методов их анализа. Краткая ...
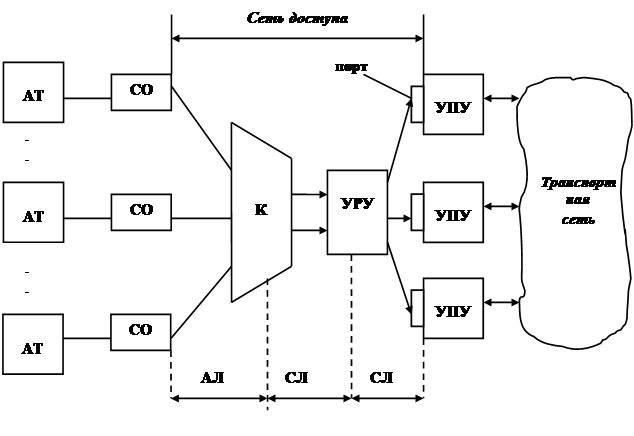
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
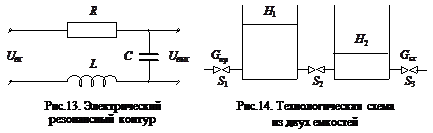



0 комментариев