Погрешности результатов измерений
Статистический анализ случайных погрешностей
Абсолютная погрешность суммы и разности равна квадратичной сумме абсолютных погрешностей
Микрокалькулятор
Проверяют вертикальность установки машины Атвуда. Балансируют грузы
По угловому коэффициенту полученной прямой определяют значение приложенной силы и сравнивают ее с реально действующей в системе
Определить по графику все значения момента силы трения и найти его среднее значение. Сравнить полученный результат с ранее измеренным в задании 1
Анализируют вклад погрешностей измерений всех величин в общую погрешность и указывают, какая из величин должна быть измерена с наибольшей точностью
В выводе сравнивают измеренное и табличное значения ускорения свободного падения
Для получения биений используют два одинаковых генератора ГЗ-33
В выводе сопоставляют измеренные и вычисленные значения скорости
Если число колебаний N в первом и втором случаях одинаково, то формулы (13.14) и (13.15) можно записать через время и число колебаний
На нижнем конце проволоки вблизи зажима белой краской наносят кольцевую метку
Навигация
Погрешности результатов измерений
Кинематика и динамика поступательного движения
136506
знаков
5
таблиц
32
изображения
1. Погрешности результатов измерений
Истинное значение физической величины обычно точно определить нельзя. Корректный способ представления результатов любого измерения состоит в том, что экспериментатор указывает свою наилучшую оценку измеряемой величины xнаил и интервал, в котором, как он уверен, она лежит:
(измеренная величина)
(1)
Например: g=9,82±0,02м/с2.
Величину Dх называют абсолютной погрешностью или доверительным интервалом определения х.
В студенческой лаборатории полученные абсолютные погрешности обычно должны округляться до одной значащей цифры, например Dg=0,02385м/с2»0,02м/с2.. Но, пожалуй, не стоит делать округление типа 0,14»0,1, ведь это сразу на 40% уменьшает погрешность.
Запись результата измерения в виде (1) необходимо делать так, чтобы последняя значащая цифра должна быть того же порядка (находиться в той же десятичной позиции), что и погрешность. Например: 92,8±0,3; 93±3; 90±30.
Очевидно, что качество измерения характеризуется не только самой абсолютной погрешностью, но также и отношением Dx к xнаил, т.е. относительной погрешностью измерения
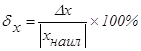. (2)
По-видимому, простейший тип учебного эксперимента - измерение величины, принятое значение которой известно. Например, эксперимент по определению скорости звука в воздухе обычно завершается сравнением измеренного значения скорости (допустим, 329±5м/с) с принятым (табличным) значением 331м/с. Очевидно, что вывод в данном случае может быть таким: «Измеренное значение скорости звука совпадает с табличным значением с точностью до погрешности измерения». Измерение может рассматриваться как удовлетворительное, даже если принятое значение слегка выходит за рамки измеренного интервала (допустим, 325±5м/с).
Во многих экспериментах измеряют два значения, которые, согласно теории должны быть равны. Две величины считаются равными, если их измеренные интервалы перекрываются. Например, импульсы р1 = 1,51±0,04 кг×м/с и р2= 1,56±0,06 кг×м/с можно
считать «равными с точностью до погрешностей измерений».
Все погрешности подразделяют на систематические, случайные и промахи.
Систематической называют такую погрешность, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Такие погрешности возникают в результате конструктивных особенностей измерительных приборов, неточности метода исследования, каких-либо упрощений экспериментатора, применении для вычислений неточных формул, округления констант. Систематические погрешности либо увеличивают, либо уменьшают результаты измерений. В любом измерительном приборе заложена та или иная систематическая погрешность, которую невозможно устранить, но которую можно учесть.
Случайные погрешности – ошибки, появление которых не может быть предупреждено, а их величина непредсказуема. Поэтому случайные погрешности могут оказать определенное влияние на отдельное измерение, но при многократных измерениях они подчиняются статистическим законам и их влияние на результаты измерений можно учесть или значительно уменьшить.
Промахи и грубые погрешности, – чрезвычайно большие ошибки, явно искажающие результаты измерения. Этот класс погрешностей вызван чаще всего неправильными действиями наблюдателя. Измерения, содержащие промахи, следует отбросить.
Для оценки полной погрешности необходимо знать и случайную и систематическую погрешности.
2. Оценка точности результатов одного прямого измерения
Если при повторении измерений в одних и тех же условиях 3 – 4 раза получено одно и то же значение, то это означает, что измерения не обнаруживают случайных изменений, а погрешность обусловлена только систематической погрешностью. Систематическая погрешность в данном случае определяется погрешностями измерительных приборов и часто называется инструментальной или приборной погрешностью. Есть несколько способов задания этой погрешности:
а) Для некоторых приборов инструментальная погрешность дается в виде абсолютной погрешности. Например, для штангенциркуля, в зависимости от конструкции его нониуса,– 0,1 мм или 0,05 мм, для микрометра – 0,01 мм.
б) Для характеристики большинства измерительных приборов часто используют понятие приведенной погрешности dп (класса точности).
Приведенная погрешность – это отношение абсолютной погрешности Dх к предельному значению хпр измеряемой величины (т.е. к наибольшему её значению, которое может быть измерено по шкале прибора). Приведенная погрешность обычно дается в процентах:
. (3)
По величине приведенной погрешности приборы разделяют на семь классов: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4.
Зная класс прибора, можно рассчитать его абсолютную погрешность. Например, вольтметр имеет шкалу делений в пределах от 0 до 300 В (хпр=300 В) и класс точности 0,5. Тогда
.
в) В некоторых случаях используется смешанный способ задания инструментальной погрешности. Например, весы технические (Т–200) имеют класс точности 2. В то же время указывается, что при нагрузке до 20 г абсолютная погрешность равна 5 мг, до 100 г – 50 мг, до 200 г – 100 мг. Набор школьных гирь относится 4-му классу точности, а допустимые погрешности масс гирь указаны в таблице 1.
Таблица 1
| Номинальное значение, г | 100 | 50 | 20 | 10 | 5 | 2 | 1 |
| Абсолютная погрешность, мг | +40 | +30 | +20 | +12 | +8 | +6 | +4 |
| Номинальное значение, г | 500 | 200 | 100 | 50 | 20 | 10 | 5 |
| Абсолютная погрешность, мг | ±3 | ±2 | ±1 | ±1 | ±1 | ±1 | ±1 |
Если, например, при взвешивании на таких весах с таким набором гирь получено значение массы тела 170 г (100 г + 50 г + 20 г), то абсолютная погрешность взвешивания равна: Dх = 40 + 30 + 20 + 100 = 200 (мг)=0,2(г).
г) В тех случаях, когда класс точности прибора не указан, абсолютная погрешность принимается равной половине цены наименьшего деления шкалы прибора. Так при измерении линейкой, наименьшее деление которой 1 мм, абсолютная погрешность равна 0,5 мм.
Похожие работы
... самопроизвольно протекать не может, необходим подвод энергии извне. 2-й закон термодинамики с использованием понятия энтропии формулируется так: Все процессы в природе протекают в направлении увеличения энтропии, энтропия замкнутой системы не может самопроизвольно уменьшаться. В статистической физике энтропию связывают с термодинамической вероятностью состояния системы – с числом ...
... в 2 раза. 180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы ...
... условий взаимной уравновешенности системы сил является одной из основных задач статики. На основе изложенной в первой главе курсовой работы алгоритм конструкции языка программирования Паскаль составим и решим ряд задач по прикладной механике. Сформулируем задачу по статике первому разделу прикладной механики. Задача. Найти центр тяжести тонкого круглого однородного стержня изогнутого по дуге ...
... тела - найти характеристики движения самого тела и отдельных его точек. В данном задании к таким характеристикам относятся векторы угловой скорости и углового ускорения тела. Рис. 1 Основные формулы кинематики плоского движения твердого тела - векторные формулы, связывающие соответственно скорости и ускорения двух произвольных точек плоской фигуры, например, точек А и В (рис. 1) B = A ...
0 комментариев