Погрешности результатов измерений
Статистический анализ случайных погрешностей
Абсолютная погрешность суммы и разности равна квадратичной сумме абсолютных погрешностей
Микрокалькулятор
Проверяют вертикальность установки машины Атвуда. Балансируют грузы
По угловому коэффициенту полученной прямой определяют значение приложенной силы и сравнивают ее с реально действующей в системе
Определить по графику все значения момента силы трения и найти его среднее значение. Сравнить полученный результат с ранее измеренным в задании 1
Анализируют вклад погрешностей измерений всех величин в общую погрешность и указывают, какая из величин должна быть измерена с наибольшей точностью
В выводе сравнивают измеренное и табличное значения ускорения свободного падения
Для получения биений используют два одинаковых генератора ГЗ-33
В выводе сопоставляют измеренные и вычисленные значения скорости
Если число колебаний N в первом и втором случаях одинаково, то формулы (13.14) и (13.15) можно записать через время и число колебаний
На нижнем конце проволоки вблизи зажима белой краской наносят кольцевую метку
Навигация
В выводе сопоставляют измеренные и вычисленные значения скорости
Кинематика и динамика поступательного движения
136506
знаков
5
таблиц
32
изображения
10. В выводе сопоставляют измеренные и вычисленные значения скорости.
11. Для проверки характера зависимость скорости волны в струне от величины натяжения строят график зависимости квадратов измеренных скорости распространения от величины ее натяжения.
ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ
Цель работы
Измерение скорости распространения звука в воздухе методом сложения перпендикулярных колебаний.
Идея эксперимента
В бегущей волне A=A0cos(wt-kl+j0) смещение колебания двух точек, находящихся на расстоянии Dl друг от друга, сдвинуты по фазе на
,
(12.1)
где V - скорость распространения волн в упругой среде, n, l - частота и длина волны.
Выражение (12.1) может быть использовано для экспериментального определения скорости распространения звука в воздухе по измерениям величин Dj,n,Dl.
Экспериментальная установка
Схема установки изображена на рисунке 27. Громкоговоритель Г, излучающий звуковые волны, закреплен на одном конце широкой трубы. Противоположный конец трубы либо открыт, либо закрыт заглушкой. Для предотвращения появления отраженной волны заглушка имеет прокладку из мягкого пористого материала (паралона). Питание громкоговорителя осуществляется от звукового генератора ЗГ. Вся установка смонтирована на измерительной скамье, вдоль которой может перемещаться микрофон М. Положение микрофона определяется с помощью масштабной линейки, укрепленной на скамье. Громкоговоритель Г испускает звуковую волну некоторой фазы j1. Эта звуковая волна достигает микрофона с фазой j2 и порождает в его цепи переменное напряжение. Между переменным напряжением на выходе звукового генератора и напряжением, возникающим в цепи микрофона, существует сдвиг фаз Dj = j2 -j1, зависящий от взаимного расположения микрофона и громкоговорителя. При перемещении микрофона по измерительной скамье на расстояние Dl = nl, составляющее целое число волн, разность фаз Dj изменяется на 2pn. Если измерить расстояние Dl между двумя положениями микрофона, соответствующее разности фаз Dj=2p, то, используя формулу (12.1), можно вычислить скорость звука в воздухе:
(12.2)
Сдвиг фаз Dj определяется по форме эллипса, описываемого на экране осциллографа электронным лучом, если вертикальные пластины осциллографа соединить с выходом звукового генератора, а горизонтальные - с микрофоном. При разности фаз Dj = 2pn
(n=0, 1, 2, ...) эллипс вырождается в прямую, проходящую через первую и третью четверти координатной плоскости, а при Dj=p(2n+1) - в прямую, проходящую через вторую и четвертую четверти.
Проведение эксперимента
Измерения и обработка результатов
1. Собирают электрическую схему установки. Микрофон располагают рядом с громкоговорителем. Подают напряжение от звукового генератора на телефон. По лимбу генератора выставляют частоту звуковых колебаний (между 1000 и 3000 Гц).
2. Медленно перемещая микрофон к противоположному концу измерительной скамьи, находят такое его положение, при котором на экране осциллографа появляется прямая линия. Делают отсчет положения микрофона.
3. Продолжая перемещать микрофон, находят несколько следующих его положений, в которых на экране осциллографа появляется такая же прямая линия, как и в первом положении.
4. Вычисляют расстояния Dl1 , Dl2 , Dl3 ... между двумя последующими положениями микрофона на измерительной скамье. Находят их среднее значение.
5. По формуле (12.2) вычисляют скорость распространения звуковой волны в воздухе. Находят погрешность ее измерения.
6. Измерения повторяют для двух других частот. Находят среднее значение скорости звука по всем измерениям.
7. Для сравнения полученного результата с табличными данными вычисляют скорость звука при условиях опыта, пользуясь соотношением
,
(12.3)
где q - температура воздуха в комнате (в кельвинах), V0 - скорость звука при 0°С (331 м/с).
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА МЕТОДОМ
КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы
Экспериментальное определение модулей сдвига различных материалов методом крутильных колебаний.
Идея эксперимента
Крутильный маятник представляет собой стержень или проволоку, верхний конец которой закреплен. К нижнему концу проволоки подвешивается тело произвольной формы. Если закрутить проволоку, т.е. вывести маятник из положения равновесия, то в системе возникнут крутильные колебания j(t). Очевидно, что период этих колебаний зависит от геометрии системы, от момента инерции подвешенного тела и от упругих свойств материала подвеса. Это позволяет, изучая крутильные колебания, определить одну из важнейших характеристик материала, – модуль сдвига.
Теория
Если момент пары сил, приложенных касательно к незакрепленному концу проволоки, равен М, то угол кручения (угловое смещение колебательной системы) по закону Гука оказывается равным j = сМ, где с – коэффициент, зависящий от упругих свойств материала проволоки. Модуль кручения f, равный
,
(13.1)
показывает, какой момент сил надо приложить, чтобы закрутить проволоку на угол в один радиан.
Модуль сдвига G равен
, (13.2)
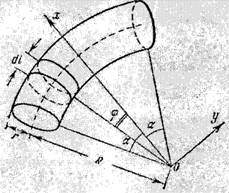
где F/S определяет величину касательной силы, приходящейся на единицу поверхности, а g - угол сдвига (рис. 28).
Между модулем кручения и модулем сдвига материала существует простое соотношение
, (13.3)
где r – радиус цилиндрической проволоки, L – ее длина.
Подвешенное на проволоке твердое тело при возникновении в системе крутильных колебаний совершает вращательные движения, к которым может быть применен основной закон динамики вращательного движения
, (13.4)
где M – вращательный момент относительно оси подвеса, J – момент инерции тела относительно той же оси, 
- угловое ускорение. Используя (13.1) и учитывая, что угловое ускорение направлено против углового смещения j, можно записать
. (13.5)
Из этого уравнения видно, что в рассматриваемом движении ускорение 
пропорционально угловой координате - смещению j и направлено противоположно ему, что является существенным признаком гармонического колебания 
, где w0 – циклическая частота. Поэтому w0 должен быть равен
,
(13.6)
где Т – период колебаний.
Далее
, (13.7)
откуда
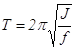. (13.8)
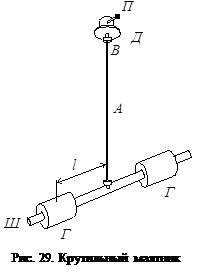В данной работе крутильный маятник представляет собой штангу Ш, подвешенную на проволоке А (рис. 29). Верхний конец проволоки закреплен с помощью винта В в держателе Д. Для выведения маятника из положения равновесия, т. е. для первоначального закручивания проволоки служит пусковое устройство П. Вдоль штанги могут перемещаться два груза Г одинаковой массы m. Изменяя расстояния l от грузов до центра штанги, можно изменять момент инерции маятника, а вместе с этим и период колебаний маятника.
Для того, чтобы из выражения (13.8) найти модуль кручения f материала проволоки, необходимо исключить неизвестный момент инерции J. Для этого в работе определяются два периода колебаний маятника при разных моментах инерции
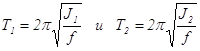, (13.9)
. (13.10)
Момент инерции крутильного маятника складывается из моментов инерции грузов 2ml2 и суммарного момента инерции штанги и проволоки j
. (13.11)
Для исключения j вычтем J1 из J2
. (13.12)
Подставляя сюда из соотношения (13.10) значение 
, получаем
.
(13.13)
. (13.14)
. (13.15)
Проведение эксперимента
Измерения
1. Подвешивают стержень крутильного маятника на выбранную проволоку. Надевают на концы штанги грузы Р. Наблюдая за положением равновесия штанги с грузами и понемногу перемещая грузы, уравновешивают штангу в горизонтальном положении. Измеряют радиус проволоки r и длину подвеса L. Записывают массы грузов m.
2. Сообщают маятнику вращательный импульс так, чтобы он совершал крутильные колебания с небольшой амплитудой. Для этого легким рывком отодвигают в сторону рычажок пускового механизма Н. Следят за тем, чтобы при пуске не возникали поступательные колебания.
3. Измеряют суммарное время t1 50-100 колебаний маятника. Измеряют расстояние l1 от оси вращения до середины одного из грузов.
4. Передвигают грузы в другое положение и, снова уравновесив маятник, измеряют время t2 такого же числа колебаний. Измеряют расстояние l2.
Похожие работы
... самопроизвольно протекать не может, необходим подвод энергии извне. 2-й закон термодинамики с использованием понятия энтропии формулируется так: Все процессы в природе протекают в направлении увеличения энтропии, энтропия замкнутой системы не может самопроизвольно уменьшаться. В статистической физике энтропию связывают с термодинамической вероятностью состояния системы – с числом ...
... в 2 раза. 180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы ...
... условий взаимной уравновешенности системы сил является одной из основных задач статики. На основе изложенной в первой главе курсовой работы алгоритм конструкции языка программирования Паскаль составим и решим ряд задач по прикладной механике. Сформулируем задачу по статике первому разделу прикладной механики. Задача. Найти центр тяжести тонкого круглого однородного стержня изогнутого по дуге ...
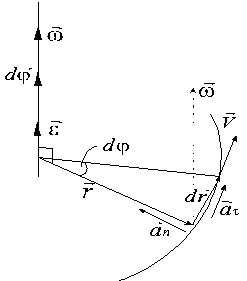
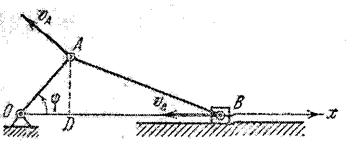
... тела - найти характеристики движения самого тела и отдельных его точек. В данном задании к таким характеристикам относятся векторы угловой скорости и углового ускорения тела. Рис. 1 Основные формулы кинематики плоского движения твердого тела - векторные формулы, связывающие соответственно скорости и ускорения двух произвольных точек плоской фигуры, например, точек А и В (рис. 1) B = A ...
0 комментариев