Навигация
59.2. Пусть
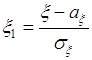 ,
, 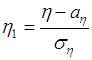 (59.5)
(59.5)
- нормированные случайные величины. Рассмотрим квадрат расстояния между ними:
![]() , (59.6)
, (59.6)
где ![]() - коэффициент корреляции случайных величин
- коэффициент корреляции случайных величин ![]() и
и ![]() . Из (59.6) следует равенство
. Из (59.6) следует равенство
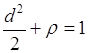 (59.7)
(59.7)
которое можно рассматривать как закон сохранения: величина ![]() - постоянная для любых случайных величин
- постоянная для любых случайных величин ![]() и
и ![]() . Это равенство позволяет дать интерпретацию коэффициента корреляции
. Это равенство позволяет дать интерпретацию коэффициента корреляции ![]() как величины, дополняющей расстояние
как величины, дополняющей расстояние ![]() до единицы.
до единицы.
Во многих приложениях теории вероятностей возникает необходимость рассматривать совокупность ![]() случайных величин
случайных величин ![]() , которая называется многомерной (
, которая называется многомерной (![]() - мерной) случайной величиной
- мерной) случайной величиной ![]() или
или ![]() -мерным случайным вектором
-мерным случайным вектором ![]() . Полное вероятностное описание
. Полное вероятностное описание ![]() - мерного случайного вектора задается функцией распределения вероятностей
- мерного случайного вектора задается функцией распределения вероятностей ![]() (или плотностью вероятности
(или плотностью вероятности ![]() , или характеристической функцией
, или характеристической функцией ![]() ). Функция
). Функция ![]() аргументов
аргументов
![]() (60.1)
(60.1)
называется функцией распределения вероятностей случайного вектора ![]() . Здесь случайное событие
. Здесь случайное событие
![]() (60.2)
(60.2)
- представляет пересечение ![]() событий вида
событий вида ![]() . В записях вида (60.1) для краткости символ пересечения
. В записях вида (60.1) для краткости символ пересечения ![]() принято заменять запятой.
принято заменять запятой.
Рассмотрим основные свойства функции распределения вероятностей.
1. Пусть ![]() - независимые случайные величины, тогда события
- независимые случайные величины, тогда события ![]() ,
, ![]() , - независимы и формула (60.1) принимает вид
, - независимы и формула (60.1) принимает вид
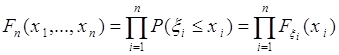 , (60.3)
, (60.3)
где ![]() - функция распределения вероятностей случайной величины
- функция распределения вероятностей случайной величины ![]() . Таким образом, для независимых случайных величин их совместная функция распределения
. Таким образом, для независимых случайных величин их совместная функция распределения ![]() представима произведением одномерных функций
представима произведением одномерных функций ![]() .
.
Для любого ![]()
![]() . (60.4)
. (60.4)
Доказательство следует из определения (60.1). Событие ![]() является невозможным, поэтому и событие (60.2) - невозможное, его вероятность равна нулю, следовательно выполняется соотношение (60.4).
является невозможным, поэтому и событие (60.2) - невозможное, его вероятность равна нулю, следовательно выполняется соотношение (60.4).
Для любого ![]()
![]() . (60.5)
. (60.5)
Это равенство также следует из определения. Событие ![]() - достоверное и в пересечении вида (60.2) это событие можно опустить, после чего из (60.1) следует (60.5).
- достоверное и в пересечении вида (60.2) это событие можно опустить, после чего из (60.1) следует (60.5).
Если ![]() для всех
для всех ![]() , то
, то
![]() , (60.6)
, (60.6)
как вероятность достоверного события.
5. Функция распределения ![]() - непрерывна справа по каждому своему аргументу.
- непрерывна справа по каждому своему аргументу.
Пусть случайный вектор ![]() имеет функцию распределения вероятностей
имеет функцию распределения вероятностей ![]() и существует частная производная
и существует частная производная
 , (61.1)
, (61.1)
тогда функция ![]() называется плотностью распределения вероятностей случайного вектора
называется плотностью распределения вероятностей случайного вектора ![]() или
или ![]() - мерной плотностью вероятности. При этом функция
- мерной плотностью вероятности. При этом функция ![]() и сам вектор
и сам вектор ![]() называются непрерывными.
называются непрерывными.
Рассмотрим основные свойства плотности вероятности случайного вектора.
1. Пусть ![]() - независимые случайные величины, тогда функция распределения вероятностей вектора
- независимые случайные величины, тогда функция распределения вероятностей вектора ![]() представима в виде произведения одномерных функций, формула (60.3). Подставляя (60.3) в (61.1), получим
представима в виде произведения одномерных функций, формула (60.3). Подставляя (60.3) в (61.1), получим
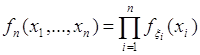 , (61.2)
, (61.2)
где
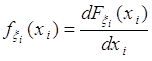 (61.3)
(61.3)
- плотность вероятности случайной величины ![]() .
.
2. Пусть ![]() - малое приращение аргумента
- малое приращение аргумента ![]() . Тогда из (61.1) следует
. Тогда из (61.1) следует
![]() , (61.4)
, (61.4)
где ![]() - разность порядка
- разность порядка ![]() функции
функции ![]() , определяемая соотношением:
, определяемая соотношением:
![]() ,
,
![]() ,…
,…
Из определения
функции ![]() , формула (60.1), следует
, формула (60.1), следует
![]()
![]() , (61.5)
, (61.5)
затем из (61.4), (61.5) получаем вероятность попадания случайного вектора ![]() в
в ![]() -мерный параллелепипед со сторонами
-мерный параллелепипед со сторонами ![]() :
:
![]() . (61.6)
. (61.6)
Из (61.6) следует
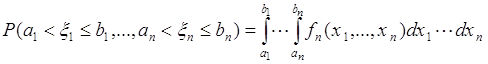 . (61.7)
. (61.7)
Похожие работы
... математического ожидания. Таким образом, (72.6) принимает вид . (72.7) 72.2. Функции вида , (72.8) где целые числа , называются начальными моментами порядка случайного процесса . Аналогично центральные моменты определяются соотношениями: . (72.9) Для функций (72.8), (72.9) используется общее название - моментные функции. Наиболее простые ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...




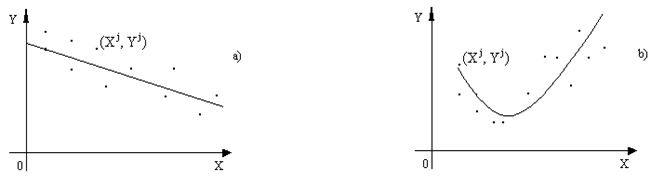
0 комментариев