Навигация
Несложно доказать следующие свойства характеристической функции
63.2 Несложно доказать следующие свойства характеристической функции.
1. ![]() .
.
2. ![]() .
.
3. Для независимых случайных величин ![]() их совместная характеристическая функция
их совместная характеристическая функция 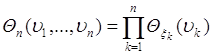 , где
, где![]()
![]() - характеристическая функция случайной величины
- характеристическая функция случайной величины ![]() .
.
4. Для любого целого ![]() ,
, ![]() , справедливо соотношение:
, справедливо соотношение:
![]() .
.
63.3. Для нормально распределенного случайного вектора ![]() его характеристическая функция находится подстановкой плотности вероятности
его характеристическая функция находится подстановкой плотности вероятности ![]() (62.1) в (63.2.) и последующем вычислении
(62.1) в (63.2.) и последующем вычислении ![]() - мерного интеграла (63.2). Это приводит к следующему выражению:
- мерного интеграла (63.2). Это приводит к следующему выражению:
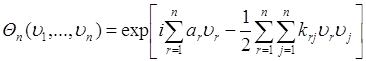 , (63.3)
, (63.3)
где ![]() - ковариация случайных величин
- ковариация случайных величин ![]() и
и ![]() .
.
Пусть ![]() - случайные величины, имеющие совместную плотность
- случайные величины, имеющие совместную плотность ![]() и совместную функцию распределения вероятностей
и совместную функцию распределения вероятностей ![]() . Пусть также заданы
. Пусть также заданы ![]() функций
функций ![]() ,
, ![]() переменных
переменных ![]() . Вместо аргументов
. Вместо аргументов ![]() функции
функции ![]() подставим случайные величины
подставим случайные величины ![]() , тогда
, тогда
![]() (64.1)
(64.1)
- новые случайные величины. Задача состоит в том, чтобы по известным функциям ![]() ,
, ![]() ,
, ![]() ,
, ![]() , найти функцию
, найти функцию ![]() и плотность
и плотность ![]() распределения вероятностей случайного вектора
распределения вероятностей случайного вектора ![]() . Такая задача довольно часто возникает во многих приложениях теории вероятностей.
. Такая задача довольно часто возникает во многих приложениях теории вероятностей.
Сравнительно просто найти функцию распределения вероятностей ![]() . Действительно, по определению:
. Действительно, по определению:
![]() (64.2)
(64.2)
Представим случайные величины ![]() через
через ![]() , используя соотношения (64.1), тогда
, используя соотношения (64.1), тогда
![]() (64.3)
(64.3)
Здесь вероятность можно представить в виде интеграла по области ![]() от плотности
от плотности ![]() :
:
![]() (64.4)
(64.4)
где область![]() содержит все
содержит все ![]() -мерные вектора
-мерные вектора ![]() , удовлетворяющие условию:
, удовлетворяющие условию:
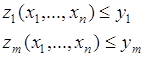 (64.5)
(64.5)
Плотность ![]() вектора
вектора ![]() можно определить из (64.4) по формуле:
можно определить из (64.4) по формуле:
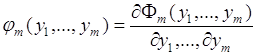 (64.6)
(64.6)
Соотношения (64.4), (64.6) определяют всего лишь метод решения задачи, но не само решение. Задача в конкретной постановке может быть как относительно простой, так и очень сложной, в зависимости от чисел ![]() ,
, ![]() , плотности
, плотности ![]() и вида функций
и вида функций ![]() , определяющих область
, определяющих область ![]() . Ниже рассмотрим примеры решения этой задачи для преобразования одной, двух и нескольких случайных величин.
. Ниже рассмотрим примеры решения этой задачи для преобразования одной, двух и нескольких случайных величин.
65.1. Пусть случайная величина ![]() имеет плотность вероятности
имеет плотность вероятности ![]() и функция одной переменной
и функция одной переменной ![]() ,
, ![]() , является взаимно однозначной, тогда плотность вероятности
, является взаимно однозначной, тогда плотность вероятности ![]() случайной величины
случайной величины ![]() определяется соотношением:
определяется соотношением:
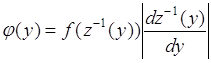 , (65.1)
, (65.1)
где ![]() - функция, обратная функции
- функция, обратная функции ![]() .
.
Вывод формулы (65.1) основан на соотношениях (64.4) и (64.6). Поскольку функция ![]() - взаимно однозначная, то эта функция или монотонно возрастающая
- взаимно однозначная, то эта функция или монотонно возрастающая ![]() или монотонно убывающая
или монотонно убывающая ![]() . Очевидны соотношения:
. Очевидны соотношения:
![]() , (65.2)
, (65.2)
![]() . (65.3)
. (65.3)
Пусть ![]() ,
, ![]() - функции распределения вероятностей случайных величин
- функции распределения вероятностей случайных величин ![]() и
и ![]() . Если
. Если ![]() , тогда используя (65.2),
, тогда используя (65.2),
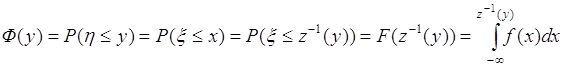 . (65.4)
. (65.4)
Продифференцируем по ![]() равенство (65.4), тогда
равенство (65.4), тогда
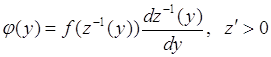 . (65.5)
. (65.5)
Аналогично при ![]() справедливо равенство (65.3), поэтому
справедливо равенство (65.3), поэтому
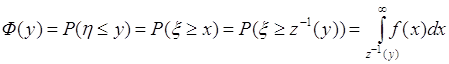 (65.6)
(65.6)
Отсюда:
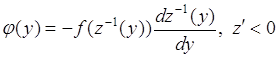 . (65.7)
. (65.7)
Теперь из соотношений (65.5) и (65.7) следует (65.1).
Существенным условием при выводе формулы (65.1) является свойство взаимной однозначности функции ![]() . Примерами таких функций являются: 1). Линейная функция
. Примерами таких функций являются: 1). Линейная функция ![]() , где
, где ![]() ,
, ![]() - числа, при этом обратная функция имеет вид
- числа, при этом обратная функция имеет вид ![]() ; 2). Экспонента -
; 2). Экспонента - ![]() , откуда обратная функция
, откуда обратная функция ![]() ,
, ![]() , и другие. Однако условие взаимной однозначности функции
, и другие. Однако условие взаимной однозначности функции ![]() может нарушаться, например, для функции
может нарушаться, например, для функции ![]() обратная функция
обратная функция ![]() ,
, ![]() - двузначная. При этом рассматриваются две функции
- двузначная. При этом рассматриваются две функции ![]() и
и ![]() ,
, ![]() , которые называются первая и вторая ветви обратного преобразования
, которые называются первая и вторая ветви обратного преобразования ![]() . Более сложный пример:
. Более сложный пример: ![]() . Здесь обратная функция – многозначная.
. Здесь обратная функция – многозначная.
65.2. Рассмотрим модификацию формулы (65.1) на случай многозначного обратного преобразования ![]() . Для этого на области определения функции
. Для этого на области определения функции ![]() выделим неперекрывающиеся интервалы
выделим неперекрывающиеся интервалы ![]() ,
, ![]() - целое, на которых
- целое, на которых ![]() , тогда на интервалах вида
, тогда на интервалах вида ![]() выполняется условие
выполняется условие ![]() . Функция
. Функция ![]() , для
, для ![]() , монотонная возрастающая, а для
, монотонная возрастающая, а для ![]() - монотонная убывающая. Поэтому для каждого из указанных интервалов существует однозначная обратная функция по отношению к функции
- монотонная убывающая. Поэтому для каждого из указанных интервалов существует однозначная обратная функция по отношению к функции ![]() . Пусть функция
. Пусть функция ![]() для
для ![]() имеет обратную функцию вида
имеет обратную функцию вида ![]() ,
, ![]() , очевидно
, очевидно ![]() - монотонная возрастающая, поскольку обратная ей
- монотонная возрастающая, поскольку обратная ей ![]() - монотонная возрастающая. Аналогично обозначим через
- монотонная возрастающая. Аналогично обозначим через ![]() - функцию со значениями
- функцию со значениями ![]() , обратную к
, обратную к ![]() на интервале
на интервале ![]() . Очевидно
. Очевидно ![]() - монотонная убывающая. Функция
- монотонная убывающая. Функция ![]() называется
называется ![]() -я ветвь обратного преобразования функции
-я ветвь обратного преобразования функции ![]() . Теперь по формуле сложения вероятностей для несовместных событий:
. Теперь по формуле сложения вероятностей для несовместных событий:
![]() (65.8)
(65.8)
где суммирование ведется по всем ветвям обратного преобразования.
На рис. 65.1. представлен простой пример функции ![]() , у которой ветви обратного преобразования:
, у которой ветви обратного преобразования: ![]() со значениями
со значениями ![]() , и
, и ![]() - со значениями
- со значениями ![]() . На интервале
. На интервале ![]() функция
функция ![]() - монотонно возрастающая, а на интервале
- монотонно возрастающая, а на интервале ![]() функция
функция ![]() - монотонная убывающая. Равенство (65.8) в этом случае принимает вид:
- монотонная убывающая. Равенство (65.8) в этом случае принимает вид:
![]() .
.
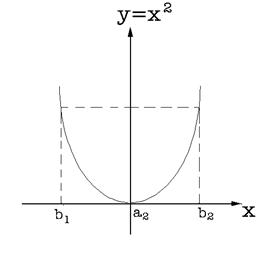
Рис. 65.1. Пример преобразования случайной величины.
Представим вероятности в (65.8) через плотности вероятностей, тогда:
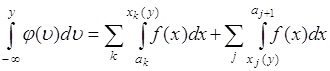 . (65.9)
. (65.9)
Дифференцируя по ![]() обе части (65.9), получим
обе части (65.9), получим
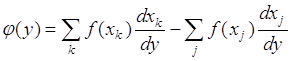 (65.10)
(65.10)
или
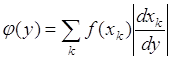 , (65.11)
, (65.11)
где суммирование по ![]() ведется по всем ветвям обратного преобразования.
ведется по всем ветвям обратного преобразования.
65.3. Рассмотрим примеры вычисления плотности вероятности случайной величины ![]() по формуле (65.11). Пусть
по формуле (65.11). Пусть ![]() - линейное преобразование случайной величины
- линейное преобразование случайной величины ![]() . Функция
. Функция ![]() - взаимно однозначная, поэтому обратное преобразование имеет одну ветвь и сумма в (65.11) содержит одно слагаемое. Поскольку
- взаимно однозначная, поэтому обратное преобразование имеет одну ветвь и сумма в (65.11) содержит одно слагаемое. Поскольку ![]() , то (65.11) принимает вид:
, то (65.11) принимает вид:
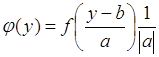 . (65.12)
. (65.12)
Рассмотрим квадратичное преобразование ![]() . Обратное преобразование имеет две ветви
. Обратное преобразование имеет две ветви ![]() и
и ![]() . Поэтому сумма (65.11) состоит из двух слагаемых. Вычисляя,
. Поэтому сумма (65.11) состоит из двух слагаемых. Вычисляя, ![]() для
для ![]() , получаем:
, получаем:
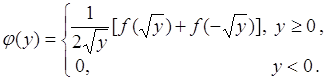 (65.13)
(65.13)
Пусть ![]() и случайная величина
и случайная величина ![]() имеет равномерное распределение вероятностей на интервале
имеет равномерное распределение вероятностей на интервале ![]() , с плотностью
, с плотностью ![]() , если
, если ![]() , и
, и ![]() при
при ![]() . Обратное преобразование имеет две ветви:
. Обратное преобразование имеет две ветви: ![]() , а также
, а также ![]()
![]() . Вычисление производных
. Вычисление производных ![]() и подстановка в (65.11) приводит к результату:
и подстановка в (65.11) приводит к результату:
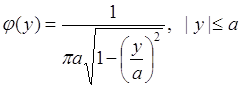 . (65.14)
. (65.14)
На рис. 65.2. представлен график плотности ![]() косинус-преобразования
косинус-преобразования
равномерно распределенной случайной величины. Таким образом, исходная
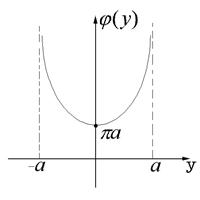
Рис. 65.2. Плотность вероятности косинус-преобразования.
исходная величина ![]() и преобразованная величина
и преобразованная величина ![]() могут иметь совершенно непохожие плотности вероятности.
могут иметь совершенно непохожие плотности вероятности.
66.1. Соотношение (65.11), определяющее плотность вероятности ![]() преобразованной величины
преобразованной величины ![]() через плотность
через плотность ![]() исходной случайной величины
исходной случайной величины ![]() , можно обобщить на случай преобразования
, можно обобщить на случай преобразования ![]() случайных величин. Пусть случайные величины
случайных величин. Пусть случайные величины ![]() имеют совместную плотность
имеют совместную плотность ![]() , и заданы
, и заданы ![]() функций
функций ![]() ,
, ![]() переменных
переменных ![]() . Необходимо найти совместную плотность вероятности
. Необходимо найти совместную плотность вероятности ![]() случайных величин:
случайных величин:
![]() (66.1)
(66.1)
Эта задача отличается от общей постановки, п. 6.4., условием ![]() - число исходных случайных величин равно числу преобразованных величин. Преобразование, обратное (66.1), находится как решение системы уравнений
- число исходных случайных величин равно числу преобразованных величин. Преобразование, обратное (66.1), находится как решение системы уравнений ![]() ,
, ![]() , относительно переменных
, относительно переменных ![]() . При этом каждое
. При этом каждое ![]() зависит от
зависит от ![]() . Совокупность таких функций
. Совокупность таких функций ![]() ,
, ![]() , образует обратное преобразование. В общем случае обратное преобразование неоднозначно. Пусть
, образует обратное преобразование. В общем случае обратное преобразование неоднозначно. Пусть ![]() ,
, ![]() , -
, - ![]() - я ветвь обратного преобразования
- я ветвь обратного преобразования ![]() , тогда справедливо соотношение:
, тогда справедливо соотношение:
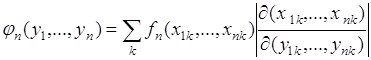 , (66.2)
, (66.2)
где сумма берется по всем ветвям обратного преобразования,
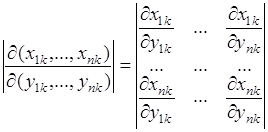 (66.3)
(66.3)
- якобиан преобразования от случайных величин ![]() к случайным величинам
к случайным величинам ![]() .
.
Если из каждой совокупности ![]() случайных величин получается
случайных величин получается ![]() случайных величин
случайных величин ![]() , то формулой (66.2) можно воспользоваться, дополнив систему
, то формулой (66.2) можно воспользоваться, дополнив систему ![]() до
до ![]() случайных величин, например, такими величинами
случайных величин, например, такими величинами ![]() . Если же
. Если же ![]() , то
, то ![]() случайных величин из совокупности
случайных величин из совокупности ![]() функционально связаны с остальными
функционально связаны с остальными ![]() величинами, поэтому
величинами, поэтому ![]() - мерная плотность
- мерная плотность ![]() будет содержать
будет содержать ![]() дельта-функций.
дельта-функций.
Соотношения (64.4), (64.6) и (66.2) определяют два метода решения задачи вычисления плотности ![]() совокупности случайных величин
совокупности случайных величин ![]() , полученных функциональным преобразованием исходных случайных величин
, полученных функциональным преобразованием исходных случайных величин ![]() с совместной плотностью вероятности
с совместной плотностью вероятности ![]() . Основная трудность в применении первого метода состоит в вычислении
. Основная трудность в применении первого метода состоит в вычислении ![]() -мерного интеграла по сложной области
-мерного интеграла по сложной области ![]() . Во втором методе основная трудность – это нахождение всех ветвей обратного преобразования.
. Во втором методе основная трудность – это нахождение всех ветвей обратного преобразования.
66.2. Рассмотрим простой пример вычисления плотности вероятности суммы двух случайных величин ![]() и
и ![]() с плотностью
с плотностью ![]() по формуле (66.2). Очевидно, в качестве первой преобразованной величины следует выбрать сумму:
по формуле (66.2). Очевидно, в качестве первой преобразованной величины следует выбрать сумму: ![]() , а в качестве второй
, а в качестве второй ![]() (хотя можно взять и
(хотя можно взять и ![]() ). Таким образом, функциональное преобразование от
). Таким образом, функциональное преобразование от ![]() ,
, ![]() к
к ![]() ,
, ![]() задается системой уравнений:
задается системой уравнений:
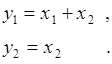 (66.4)
(66.4)
Обратное преобразование – это решение системы уравнений относительно ![]() ,
, ![]() :
:
 (66.5)
(66.5)
Обратное преобразование однозначно, поэтому в (66.2) сумма состоит из одного слагаемого. Найдем якобиан преобразования:
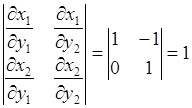 .
.
Теперь (66.2) для ![]() принимает вид:
принимает вид:
![]() . (66.6)
. (66.6)
Функция ![]() - это совместная плотность вероятности случайных величин
- это совместная плотность вероятности случайных величин ![]() и
и ![]() . Отсюда плотность вероятности
. Отсюда плотность вероятности ![]() суммы
суммы ![]() находится из условия согласованности:
находится из условия согласованности:
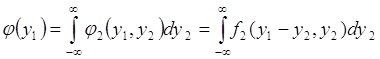 . (66.7)
. (66.7)
Рассмотрим первый метод решения этой же задачи. Из (64.4) следует:
![]() . 66.8)
. 66.8)
Задача сводится к преобразованию интеграла по области ![]() , определяемой условием
, определяемой условием ![]() . Этот интеграл можно представить в виде:
. Этот интеграл можно представить в виде:
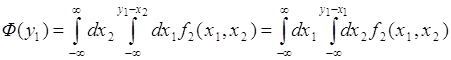 (66.9)
(66.9)
Отсюда плотность вероятности:
Отсюда плотность вероятности:
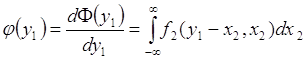 , (66.10)
, (66.10)
что совпадает с формулой (66.7).
Хи - квадрат распределение вероятностей
67.1. Хи - квадрат распределением с ![]() степенями свободы называется распределение вероятностей случайной величины
степенями свободы называется распределение вероятностей случайной величины ![]() , где
, где ![]() - независимые случайные величины и все
- независимые случайные величины и все ![]() - гауссовы с математическим ожиданием
- гауссовы с математическим ожиданием ![]() и дисперсией
и дисперсией ![]() . В соответствии с формулой (64.3) функция распределения вероятностей случайной величины
. В соответствии с формулой (64.3) функция распределения вероятностей случайной величины ![]() равна
равна
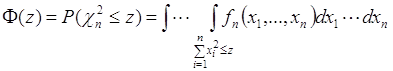 , (67.1)
, (67.1)
где ![]() - совместная плотность вероятности величин
- совместная плотность вероятности величин ![]() . По условию
. По условию ![]() - независимые, поэтому
- независимые, поэтому ![]() равна произведению одномерных плотностей:
равна произведению одномерных плотностей:
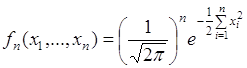 . (67.2)
. (67.2)
Из (67.1), (67.2) следует, что плотность вероятности ![]() случайной величины
случайной величины ![]() определяется выражением:
определяется выражением:
 . (67.3)
. (67.3)
Анализ этого выражения, видимо, представляет собой наиболее простой способ нахождения ![]() , поскольку здесь
, поскольку здесь ![]() и (67.3) можно представить в виде:
и (67.3) можно представить в виде:
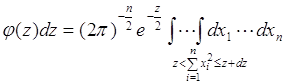 . (67.4)
. (67.4)
Здесь интеграл равен объему ![]() области
области ![]() - мерного пространства, заключенной между двумя гиперсферами:
- мерного пространства, заключенной между двумя гиперсферами:  - радиуса
- радиуса ![]() и
и 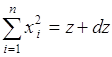 - радиуса
- радиуса ![]() . Поскольку объем
. Поскольку объем ![]() гиперсферы радиуса
гиперсферы радиуса ![]() пропорционален
пропорционален ![]() , т.е.
, т.е. ![]() , то
, то
![]() (67.5)
(67.5)
- объем между двумя гиперсферами с радиусами ![]() и
и ![]() , что и определяет с точностью до множителя интеграл (67.4). Подставим (67.5) в (67.4), тогда
, что и определяет с точностью до множителя интеграл (67.4). Подставим (67.5) в (67.4), тогда
![]() , (67.6)
, (67.6)
где ![]() - постоянная, которая может быть определена из условия нормировки:
- постоянная, которая может быть определена из условия нормировки:
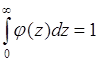 . (67.7)
. (67.7)
Подставим (67.6) в (67.7), тогда
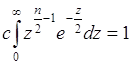 . (67.8)
. (67.8)
Пусть ![]() ,
, ![]() , тогда интеграл (67.8)
, тогда интеграл (67.8)
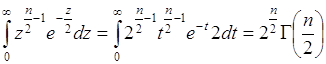 , (67.9)
, (67.9)
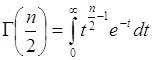 , (67.10)
, (67.10)
где ![]() - гамма - функция аргумента
- гамма - функция аргумента ![]() . Из (67.8) и (67.9) определяется постоянная
. Из (67.8) и (67.9) определяется постоянная ![]() , подстановка которой в (67.6) приводит к результату
, подстановка которой в (67.6) приводит к результату
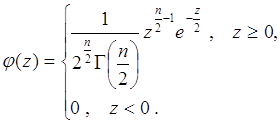 (67.11)
(67.11)
67.2. Вычислим математическое ожидание и дисперсию случайной величины ![]() . Из (67.11)
. Из (67.11)

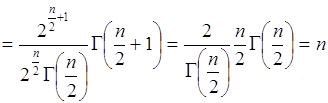 . (67.12)
. (67.12)
Аналогично среднее квадрата величины ![]() равно
равно
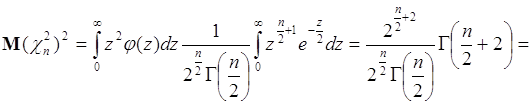
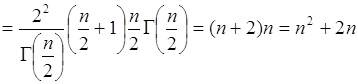 . (67.13)
. (67.13)
Из (67.12), (67.13) дисперсия
![]() . (67.14)
. (67.14)
67.3. В задачах математической статистики важное значение имеют распределения вероятностей, связанные с нормальным распределением. Это прежде всего ![]() - распределение (распределение Пирсона),
- распределение (распределение Пирсона), ![]() - распределение (распределение Стьюдента) и
- распределение (распределение Стьюдента) и ![]() - распределение (распределение Фишера). Распределение
- распределение (распределение Фишера). Распределение ![]() - это распределение вероятностей случайной величины
- это распределение вероятностей случайной величины
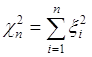 , (67.15)
, (67.15)
где ![]() - независимы и все
- независимы и все ![]() .
.
Распределением Стьюдента (или ![]() - распределением) называется распределение вероятностей случайной величины
- распределением) называется распределение вероятностей случайной величины
 , (67.16)
, (67.16)
где ![]() и
и ![]() - независимые случайные величины,
- независимые случайные величины, ![]() и
и ![]() .
.
Распределением Фишера (![]() - распределением) с
- распределением) с ![]() ,
, ![]() степенями свободы называется распределение вероятностей случайной величины
степенями свободы называется распределение вероятностей случайной величины
 . (67.17)
. (67.17)
Распределение Максвелла по скоростям молекул газа представляет собой плотность распределения вероятностей модуля скорости ![]() и определяется соотношением
и определяется соотношением
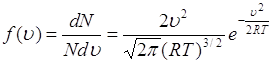 , (68.1)
, (68.1)
где ![]() - число молекул газа,
- число молекул газа, ![]() число молекул, модуль скорости которых лежит в интервале
число молекул, модуль скорости которых лежит в интервале ![]() ,
, ![]() - газовая постоянная,
- газовая постоянная, ![]() - абсолютная температура газа. Отношение
- абсолютная температура газа. Отношение ![]() - это вероятность того, что модуль скорости молекулы лежит в интервале
- это вероятность того, что модуль скорости молекулы лежит в интервале ![]() , тогда
, тогда ![]() - плотность вероятности модуля скорости.
- плотность вероятности модуля скорости.
Распределение (68.1) может быть получено на основе следующих двух простых вероятностных положений, задающих модель идеального газа. 1). Проекции ![]() скорости на оси
скорости на оси ![]() декартовой системы координат являются независимыми случайными величинами. 2). Каждая проекция скорости
декартовой системы координат являются независимыми случайными величинами. 2). Каждая проекция скорости ![]() - гауссова случайная величина с нулевым математическим ожиданием и дисперсией
- гауссова случайная величина с нулевым математическим ожиданием и дисперсией ![]() . Параметр
. Параметр ![]() задается на основе экспериментальных данных.
задается на основе экспериментальных данных.
Определим плотность вероятности случайной величины
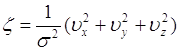 . (68.2)
. (68.2)
Очевидно, ![]() имеет хи - квадрат распределение с тремя степенями свободы. Поэтому ее плотность вероятности
имеет хи - квадрат распределение с тремя степенями свободы. Поэтому ее плотность вероятности ![]() определяется формулой (67.11) при
определяется формулой (67.11) при ![]() :
:
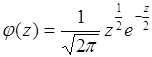 ,
, ![]() , (68.3)
, (68.3)
поскольку ![]() . Итак,
. Итак, ![]() (68.3) - это плотность вероятности квадрата относительной скорости
(68.3) - это плотность вероятности квадрата относительной скорости ![]() .
.
Следующий шаг состоит в переходе от распределения квадрата скорости ![]() к распределению ее модуля
к распределению ее модуля ![]() ,
, ![]() . Функциональное преобразование имеет вид:
. Функциональное преобразование имеет вид: ![]() , а обратное
, а обратное ![]() , для
, для ![]() ,
, ![]() . Таким образом, обратное преобразование однозначное. Поэтому по (65.1) плотность распределения модуля
. Таким образом, обратное преобразование однозначное. Поэтому по (65.1) плотность распределения модуля ![]() имеет вид
имеет вид
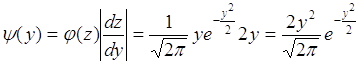 . (68.4)
. (68.4)
Последний шаг состоит в переходе от случайной величины ![]() к новой случайной величине
к новой случайной величине
![]() . (68.5)
. (68.5)
Обратное преобразование ![]() - однозначное, поэтому плотность вероятности
- однозначное, поэтому плотность вероятности ![]() случайной величины
случайной величины ![]() , согласно (65.1) принимает вид
, согласно (65.1) принимает вид
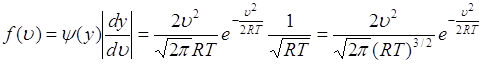 ,
, ![]() , (68.6)
, (68.6)
что и совпадает с формулой (68.1).
Соотношение (68.5), определяющее связь относительной и абсолютной скоростей ![]() и
и ![]() , следует из третьего положения модели идеального газа, которое является чисто физическим условием, в отличие от первых двух вероятностных условий. Третье условие может быть сформулировано как утверждение относительно значения
, следует из третьего положения модели идеального газа, которое является чисто физическим условием, в отличие от первых двух вероятностных условий. Третье условие может быть сформулировано как утверждение относительно значения ![]() средней кинетической энергии одной молекулы в виде равенства
средней кинетической энергии одной молекулы в виде равенства
![]() , (68.7)
, (68.7)
где ![]() - постоянная Больцмана и представляет, по сути, экспериментальный факт. Пусть
- постоянная Больцмана и представляет, по сути, экспериментальный факт. Пусть ![]() , где
, где ![]() - постоянная, которая далее определяется условием (68.7). Для нахождения
- постоянная, которая далее определяется условием (68.7). Для нахождения ![]() определим из (68.4) среднее квадрата относительной скорости:
определим из (68.4) среднее квадрата относительной скорости:
 . (68.8)
. (68.8)
Тогда средняя кинетическая энергия молекулы ![]() , где
, где ![]() - масса молекулы, и с учетом (68.7)
- масса молекулы, и с учетом (68.7) ![]() , или
, или ![]() .
.
1. Вентцель Е.С. Теория вероятностей: Учебник для вузов. М.: Высшая школа, 1999. - 575с.
2. Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика. М.: Высшая школа, 1973. - 368с.
3. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения М.: Высшая школа, 2000. - 480с.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1999. - 479с.
5. Пытьев Ю.П., Шишмарев И.А. Курс теории вероятностей и математической статистики для физиков. М.: Изд-во Моск. ун-та, 1983. - 256с.
6. Пугачев В.С. Теория вероятностей и математическая статистика. М.: Наука, 1979. - 496с.
7. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. М.: Высшая школа, 1991. - 400с.
8. Фигурин В.А., Оболонкин В.В. Теория вероятностей и математическая статистика. М.: Новое знание, 2000. - 206с.
9. Чистяков В.П. Курс теории вероятностей. М.: Наука, 1982. - 256с.
10. Боровков А.А. Теория вероятностей. М.: Наука, 1976. - 352с.
11. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ, 2000. - 543с.
Похожие работы
... математического ожидания. Таким образом, (72.6) принимает вид . (72.7) 72.2. Функции вида , (72.8) где целые числа , называются начальными моментами порядка случайного процесса . Аналогично центральные моменты определяются соотношениями: . (72.9) Для функций (72.8), (72.9) используется общее название - моментные функции. Наиболее простые ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
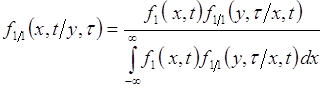




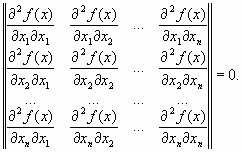
0 комментариев