Навигация
Решение системы линейных уравнений методом Ритца
5. Решение системы линейных уравнений методом Ритца
Если ![]() - симметричная и положительно-определённая матрица, то задача решения линейной системы уравнений:
- симметричная и положительно-определённая матрица, то задача решения линейной системы уравнений:
![]() (36)
(36)
эквивалентна задаче нахождения точки минимума функции многих переменных:
![]() (37)
(37)
где скалярные произведения понимаются в смысле ![]() , т.е.
, т.е.
![]() (38)
(38)
Иначе говоря, решение системы линейных уравнений (36) доставляет минимум функции многих переменных:
![]() (39)
(39)
И наоборот, точка минимума функции (39) является решением системы линейных уравнений (36).
Таким образом, метод Ритца позволяет решение линейной системы уравнений с симметричной и положительно-определённой матрицей свести к задаче нахождения точки минимума функций многих переменных. А эту задачу мы уже умеем решать.
6. Решение системы линейных уравнений с трехдиаганальной матрицей методом прогонки Томаса
При решении задач конечно-разностными методами или методом конечных элементов, часто решение задачи сводится к решению линейной системы уравнений с трехдиаганальной матрицей коэффициентов, т.е. с матрицей, где все элементы нули, кроме трех диагоналей (в окрестности главной диагонали); рассмотрим систему с трехдиаганальной матрицей:
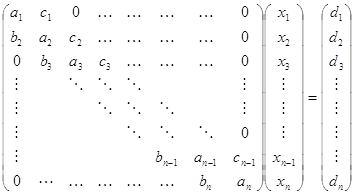 (40)
(40)
для решения этой линейной системы уравнений, конечно, можно применять метод Гаусса, но тогда пришлось бы делать много необязательных операций с нулями. Чтобы сэкономить время вычислений и не работать лишний раз с нулями, Томас (1949г.) разработал специальный алгоритм расчета. Рассчитывая по алгоритму Томаса элементы получаемой треугольной матрицы, мы следуем методу Гаусса, с уточнением, что с нулями никаких действий не производим; алгоритм Томаса называют – методом прогонки.
Для решения системы (40) методом прогонки – Томаса действуем следующим образом:
а) прямой ход:
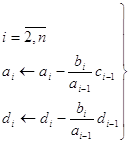 (41)
(41)
Замечание: после проведения прямого хода предполагается, что все ![]() , и
, и ![]() - неизменны (что очевидно).
- неизменны (что очевидно).
б) обратный ход:
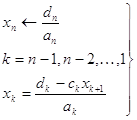 (42)
(42)
Таким образом, для системы линейных уравнений с трехдиаганальной матрицей наиболее экономным является алгоритм прогонки – Томаса, который является «отфильтрованным» методом Гаусса.
Метод минимизации невязки для решения линейной системы уравнений (метод наименьших квадратов).
При проведении экспериментов, часто приходится решать следующую задачу: определить ![]() известных
известных ![]() ,которые непосредственно не измеряются, а измеряются величины
,которые непосредственно не измеряются, а измеряются величины ![]() связанные с определяемыми переменными
связанные с определяемыми переменными ![]() . Измерения не свободны от случайных ошибок, которыми нельзя пренебречь.
. Измерения не свободны от случайных ошибок, которыми нельзя пренебречь.
Число наблюдаемых величин больше числа неизвестных ![]() . Пусть известно, что величины
. Пусть известно, что величины ![]() связаны между собой линейной зависимостью:
связаны между собой линейной зависимостью:
![]() ,
, ![]() ,
, ![]() . (43)
. (43)
Коэффициенты ![]() - считаются известными и неотягощенными случайными ошибками. Система (43) называется системой условных уравнений.
- считаются известными и неотягощенными случайными ошибками. Система (43) называется системой условных уравнений.
Если бы все числа ![]() были точными, то неизвестные
были точными, то неизвестные ![]() ,
, ![]() могли бы быть определены из любых
могли бы быть определены из любых ![]() - уравнений системы
- уравнений системы ![]() . Но так, как
. Но так, как ![]() - определены с ошибками, то система условных уравнений несовместна (переопределена, т.к.
- определены с ошибками, то система условных уравнений несовместна (переопределена, т.к. ![]() ), существуют «невязки»:
), существуют «невязки»:
![]() ,
, ![]()
![]() (44)
(44)
задача теперь заключается в том, чтобы найти такие значения ![]() , при которых функция невязки
, при которых функция невязки ![]() - минимально по некоторой норме, т.е. мы ищем такие
- минимально по некоторой норме, т.е. мы ищем такие ![]() , при которых норма невязки
, при которых норма невязки ![]() - минимальна.
- минимальна.
В методе наименьших квадратов, в качестве нормы рассматривают дискретную норму Гаусса:
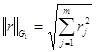 (45)
(45)
Очевидно, что эта норма минимальна тогда, когда минимально подкоренное выражение, т.е. сумма квадратов невязок ![]() .
.
![]() (46)
(46)
Условия существования минимума для функций специального вида ![]() имеют вид:
имеют вид:
![]() ,
,![]() ,
(47)
,
(47)
т.е. задача сводится, как и в общей теории приближений, к решению системы нормальных уравнений.
Для примера рассмотрим ![]() уравнений с тремя неизвестными, система условных уравнений имеет вид:
уравнений с тремя неизвестными, система условных уравнений имеет вид:
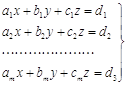 (48)
(48)
Тогда система соответствующих нормальных уравнений имеет вид:
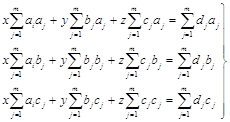 (49)
(49)
Решение системы (49) дает решение задачи (48) наилучшим приближением, в смысле дискретной нормы Гаусса.
Замечания:
1) классический метод Гаусса, метод Гаусса с выбором главного элемента, метод Якоби и метод минимизации невязки являются общими методами и применяются для определения решения невырожденных систем линейных уравнений, когда ведущие (большие по модулю) элементы матрицы системы расположены в окрестности главной диагонали (система хорошо обусловлена), если же система плохо обусловлена, тогда нужно менять соответствующую модель, чтобы она приводила к приемлемой системе уравнений;
2) для ускорения сходимости методов разработаны специальные методы – метод Гаусса-Зейделя, методы релаксации и др., которые применимы лишь для узкого класса систем – с симметрической, положительно-определенной матрицей; с ненулевыми диагональными элементами;
3) для нужд разностных уравнений разработаны специальные алгоритмы прогонки Томаса, которые являются «экономными» методами Гаусса для трехдиагональных матриц системы линейных уравнений.
Литература
1. Т. Шуп. Решение интегральных задач на ЭВМ. Мир., М.,2002
2. Л. Коллатц, Ю. Альберхт. Задачи по прикладной математике. Мир., М.,1998.
3. Т.А. Обгадзе. Элементы математического моделирования. Учебное пособие. Грузинский Политехнический Институт им. В.И. Ленина, Тбилисси, 1999.
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... , с помощью которых в последующем решение систем линейных уравнений станет намного проще, понятнее и быстрее. Цель моей работы заключается в том, чтобы изучить различные способы решения систем линейных уравнений для применения их на практике. Для достижения любой цели необходимо выполнить какие-то определенные задачи. Мне нужно выполнить следующие задачи: исследовать литературу по темам матриц, ...
... , придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д. Если работа в поисках более рациональный способ решения систем линейных уравнений с двумя переменными - методом подстановки будет успешна, то практическая значимость будет очевидна. Список использованной литературы 1. Алгебра 8 класс. Н.Я. Виленкин. Москва, ...
... 10.4 9.7 9.7 -8.4 Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = b1 , a21x2 + ...

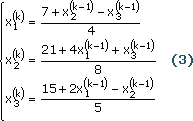
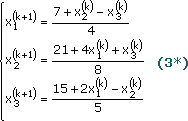
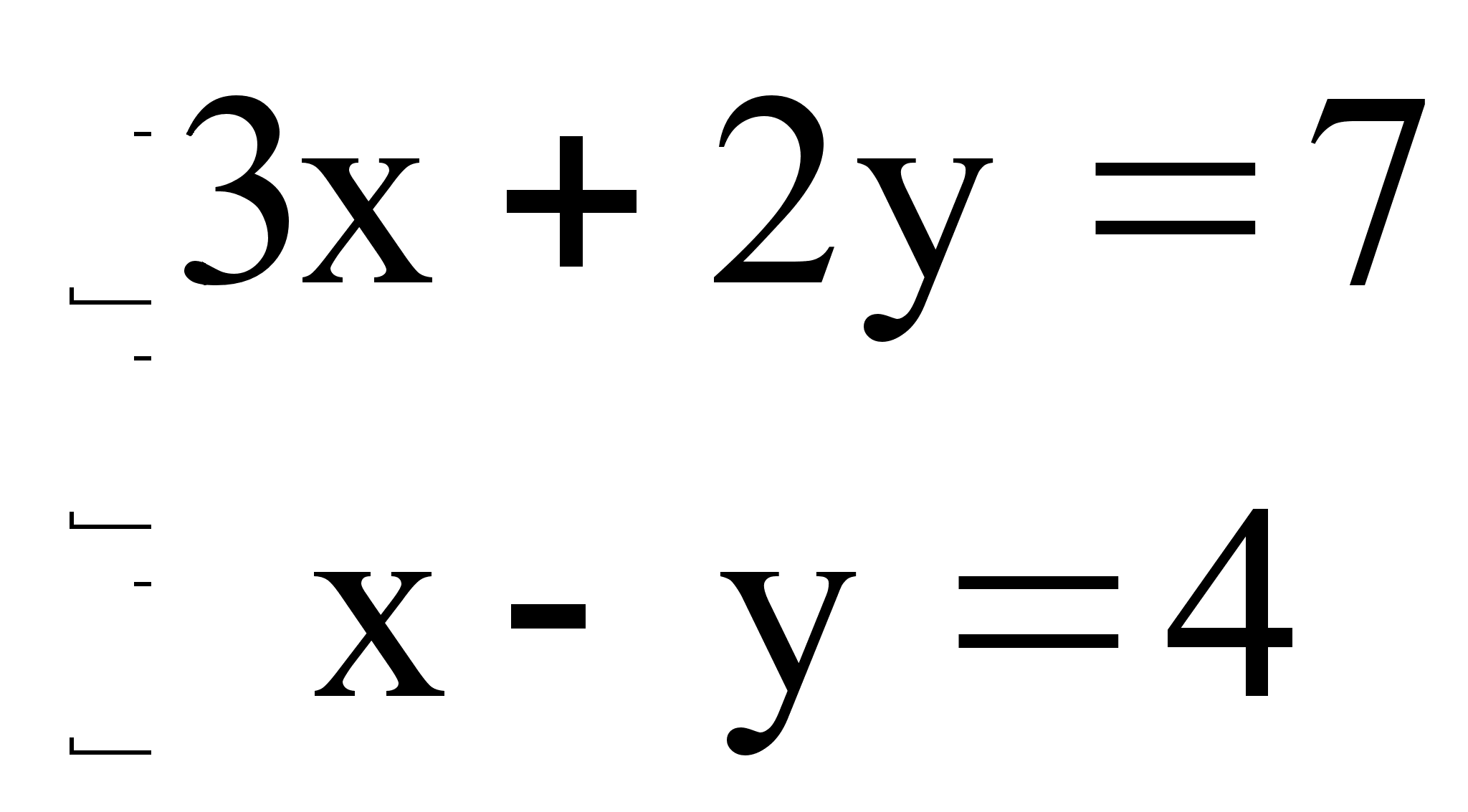
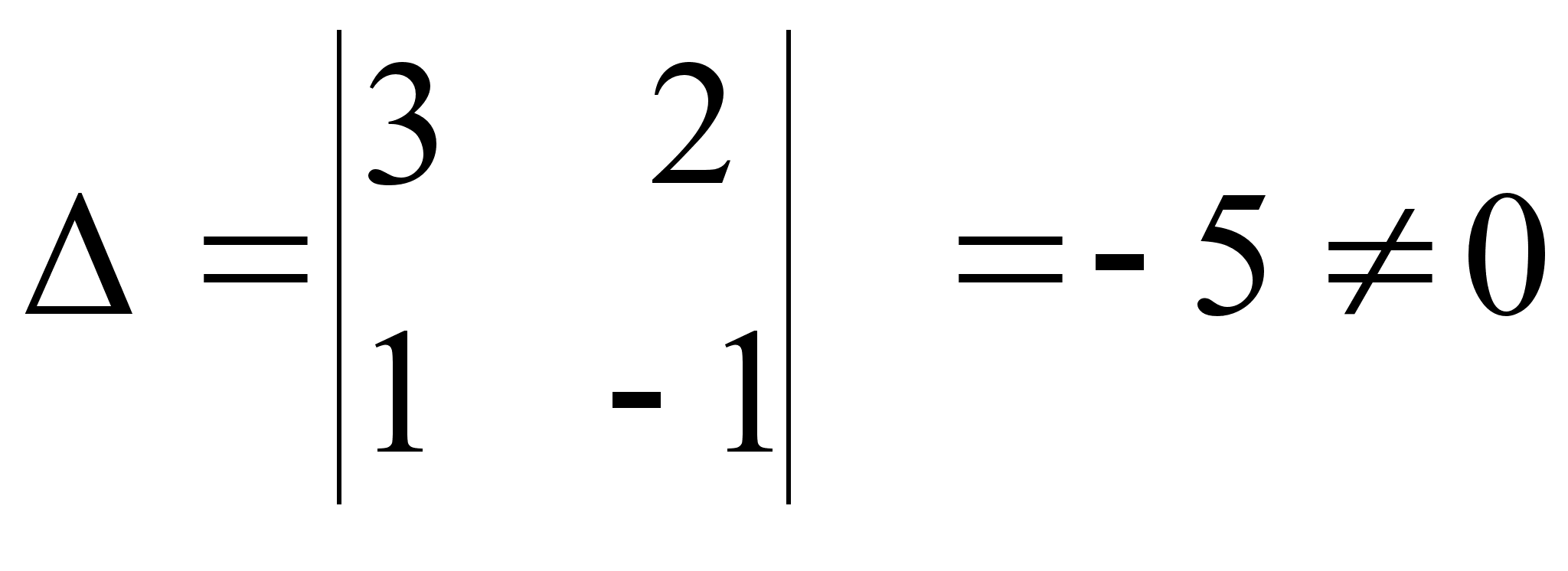
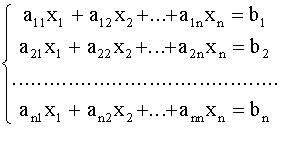



0 комментариев