Навигация
Распределение Пуассона. Аксиомы простейшего потока событий
Министерство образования и науки Украины
Харьковский национальный университет радиоэлектроники
Факультет ПММ
Кафедра ПМ
КУРСОВАЯ РАБОТА
Тема: Распределение Пуассона. Аксиомы простейшего потока событий.
Дисциплина: Теория вероятностей и математическая статистика
Выполнил: Проверил:
ст. группы ******** проф. **********
*****************
Харьков 2007
РЕФЕРАТ
В данном курсовом проекте представлено описание понятий корреляционного момента и его свойств, коэффициента корреляции, случайных событий и их основных числовых характеристик, применения на практике корреляции, а также приведено решение практических задач.
Пояснительная записка состоит из вступления, основной части, выводов, списка литературы.
Записка 28с.
Ключевые слова и выражения:
СЛУЧАЙНАЯ ВЕЛИЧИНА, МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, ДИСПЕРСИЯ, НАЧАЛЬНЫЙ МОМЕНТ, ЦЕНТРАЛЬНЫЙ МОМЕНТ, КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ, КОРРЕЛЯЦИОННЫЙ МОМЕНТ, ЗАКОН РАСПРЕДЕЛЕНИЯ, СРЕДНЕЕ КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ, ЗАВИСИМОСТЬ.
СОДЕРЖАНИЕ
Введение………………………………………………………………………..….41 Теоретическая часть……….……………………………………………………5
1.1 Доверительные оценки…………………………………………..……….….5
1.2 Метод наибольшего правдоподобия………………………………….…...10
1.3 Точечные оценки…………………………………………………………..13
1.4 Критерий согласия…………………………………………………….……18
1.5 Теорема Чебышева…………………………………………...……….……19
1.6 Понятие доверительного интервала………………...……………….….…23
1.7 Сравнение средних………………………………………………………....25
1.8 Метод минимума X2 ……………………………………………………..…26
1.9 Распределение Пуассона. Аксиомы простейшего потока событий…..…28
2 Практическая часть……………………………………………………………30
Выводы…………………………………………………………………………...37
Список литературы……………………………………………………………...38
ВВЕДЕНИЕ
Теория вероятности – математическая наука, изучающая закономерности в случайных явлениях. При научном исследовании физических и технических задач, часто приходится встречаться с явлениями особого типа, которые принято называть случайными. Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает несколько по-иному.
Очевидно, что в природе нет ни одного физического явления, в котором не присутствовали бы в той или иной мере элементы случайности. Как бы точно и подробно ни были фиксированы условия опыта, невозможно достигнуть того, чтобы при повторении опыта результаты полностью и в точности совпадали.
Случайности неизбежно сопутствуют любому закономерному явлению. Тем не менее, в ряде практических задач этими случайными элементами можно пренебречь, рассматривая вместо реального явления его упрощенную схему, т.е. модель, и предполагая, что в данных условиях опыта явление протекает вполне определенным образом. При этом из бесчисленного множества факторов, влияющих на данное явление, выделяют самые главные, решающие. Влиянием остальных, второстепенных факторов просто пренебрегают. Изучая закономерности в рамках некоторой теории, основные факторы, влияющие на то или иное явление, входят в понятия или определения, которыми оперирует рассматриваемая теория.
Как и всякая наука, развивающая общую теорию какого-либо круга явлений, теория вероятностей также содержит ряд основных понятий, на которых она базируется. Естественно, что не все основные понятия могут быть строго определены, так как определить понятие – это значит свести его к другим, более известным. Этот процесс должен быть конечным и заканчиваться на первичных понятиях, которые только объясняются.
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ1.1 Доверительные оценки
Выборочная оценка, являясь точечной, дает оценочные значения соответствующего параметра из данной выборки, но ничего не дает для точности и достоверности оценки. Такие данные поставляют доверительные оценки. Пусть ![]() случайная выборка из генеральной совокупности со случайной величиной
случайная выборка из генеральной совокупности со случайной величиной ![]() , распределение которой зависит от параметра
, распределение которой зависит от параметра ![]() . Пусть
. Пусть ![]() – такие функции выборок, что при произвольном
– такие функции выборок, что при произвольном ![]() выполняется равенство
выполняется равенство
![]() . (1.1.1)
. (1.1.1)
Тогда случайный интервал ![]() называется доверительной оценкой параметра
называется доверительной оценкой параметра ![]() с мерой надежности
с мерой надежности ![]() (с уровнем значимости
(с уровнем значимости ![]() ).
).
Если имеется реализация ![]() выборки
выборки ![]() , то реализация доверительной оценки дает доверительный интервал
, то реализация доверительной оценки дает доверительный интервал ![]() и в большом ряду выборок истинное значение лежит примерно в
и в большом ряду выборок истинное значение лежит примерно в ![]() случаев внутри вычисленных доверительных границ
случаев внутри вычисленных доверительных границ ![]() и
и ![]() . Равенство (1.1.1) можно интерпретировать и так: случайный интервал
. Равенство (1.1.1) можно интерпретировать и так: случайный интервал ![]() “покрывает” истинный параметр с доверительной вероятностью
“покрывает” истинный параметр с доверительной вероятностью ![]() .
.
В математической статистике часто используют понятие квантилей, процентных точек (односторонних критических границ и двухсторонних критических границ). Квантилью уровня p или p–квантилью ![]() случайной величины
случайной величины ![]() с функцией распределения
с функцией распределения ![]() называется решение уравнения
называется решение уравнения ![]() .
.
Односторонней критической границей, отвечающей уровню значимости ![]() (процентной точкой уровня
(процентной точкой уровня ![]() ),
непрерывной случайной величины
),
непрерывной случайной величины ![]() с функцией распределения
с функцией распределения ![]() называется значение случайной величины
называется значение случайной величины ![]() , для которой
, для которой ![]() , или
, или ![]() . Нижней и верхней критическими границами, отвечающими уровню значимости
. Нижней и верхней критическими границами, отвечающими уровню значимости ![]() непрерывной случайной величины
непрерывной случайной величины ![]() с функцией распределения
с функцией распределения ![]() называются значения случайной величины
называются значения случайной величины ![]() и
и ![]() , для которых
, для которых ![]() ;
; ![]() ;
;
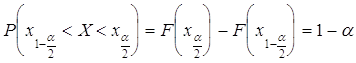 .
.
Для симметричных случайных величин, у которых плотности
распределения симметричны относительно некоторой точки![]() , нижние и верхние критические границы удовлетворяют условию
, нижние и верхние критические границы удовлетворяют условию ![]() , что дает возможность приводить таблицы лишь для процентных точек или квантилей, больших
, что дает возможность приводить таблицы лишь для процентных точек или квантилей, больших ![]() . Так, для стандартной нормальной случайной величины с уровнем значимости
. Так, для стандартной нормальной случайной величины с уровнем значимости ![]()
![]() .
.
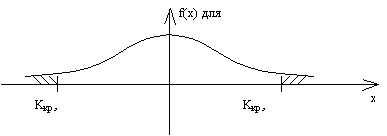
Квантиль, односторонние и двухсторонние критические границы изображены на рис.1.
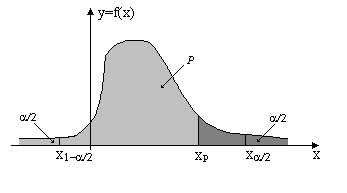
Рис.1. р-квантиль и критические точки для закона распределения ![]() .
.
Похожие работы
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... по соответствующему полю). В окне Конструктора таблиц созданные связи отображаются визуально, их легко изменить, установить новые, удалить (клавиша Del). 1 Многозвенные информационные системы. Модель распределённого приложения БД называется многозвенной и её наиболее простой вариант – трёхзвенное распределённое приложение. Тремя частями такого приложения являются: ...
... , вторая в среднем убывает. 3. D(x±h)=D(x)+D(h)±2mxh Доказательство. D(x±h)=M((x±h)2)—M2(x±h)=M(x2±2xh+h2)—(M(x)±M(h))2=M(x2)±2M(xh)+M(h2)—+M2(x)+2M(x)*M(h)—M2(h)=D(x)+D(h)±2(M(xh))—M(x)*M(h)=D(x)+D(h)±2mxh Вопрос 31 Мат. статистика опирается на теорию вероятностей, и ее цель – оценить характеристики генеральной совокупности по выборочным данным. Генеральной совокупностью называется ...
... поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
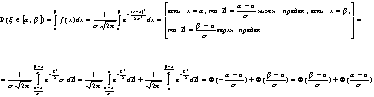



0 комментариев