Навигация
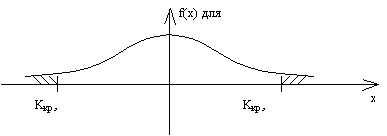
1.4 Критерии согласия
Пусть (X1,..,Xn) - выборка с неизвестным законом распределения F(X). Рассмотрим гипотезы Н0: F(x)=F0(x) при конкурирующей Н1: F(x)¹F0(x). F0(x)- некоторая заданная функция распределения.
Задача проверки гипотез относительно законов распределения называется задачей проверки согласия, а критерий для этой задачи - –ритерием согласия.
Рассмотрим критерий согласия c2, или критерий Пирсона.
Разобьем ось х на т интервалов 
Если истинная функция распределения F(x) совпадает с F0(x), то при больших n
Рассмотрим случайную величину (ni - –лучайное)
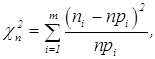
при 
она стремится к c2 - –аспределению случайной величины с т-е-1 степенями свободы (е- число статистических параметров).
Решающее правило для уровня значимости a:
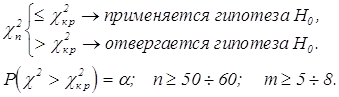
При построении c2n должно выполняться условие ni³10, в противном случае объединяют интервалы.
В случае применения гипотезы Н0 говорят, что различие между F(x) и F0(x) является случайным с доверительной вероятностью 1-a и обусловлено конечностью выборки.
1.5 Теорема Чебышева
Неравенство Чебышева. Для любой случайной величины Х, имеющей математическое ожидание МХ и дисперсию DX, справедливо неравенство
где a — любое положительное число.
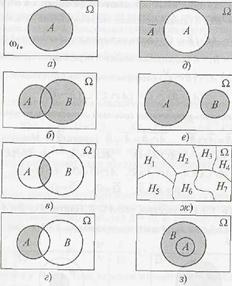
Доказательство. Доказательство проведём сначала для непрерывной случайной величины Х с плотностью распределения f(x).
Обозначим через А событие, состоящее в том, что случайная точка Х попадает за пределы участка (MX-a; MX+a), то есть
А: {|X-MX|³a}
a a
 | ||
 | ||
MX -a MX MX+a
Вероятность попадания Х в этот участок равна
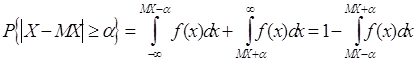
Найдём дисперсию случайной величины Х
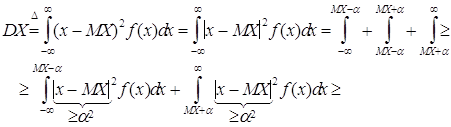
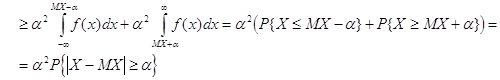
Совершенно аналогично доказывается неравенство Чебышева и для дискретной случайной величины, имеющей значения x1, x2, ... с вероятностями p1, p2, ... Тогда вместо интеграла во всех формулах ставится знак суммы, где суммирование ведётся по тем xi , для которых
|xi-MX|³a,
что и требовалось доказать.
Определение. Пусть имеется последовательность чисел
x1, x2, ... , xn , ...
Говорят, что эта последовательность сходится по вероятности к неслучайной величине а, если при неограниченном увеличении п вероятность события
{|Хп-а|< e},
(где e>0 - произвольное малое фиксированное число) стремится к единице, то есть
Иными словами, каковы бы ни были произвольно малые наперёд заданные числа e>0 и d>0 всегда существует N, такое, что при n>N
P{|Xn-a|<e}>1-d
Первая теорема Чебышева (Закон больших чисел). Пусть имеется случайная величина Х с медианой МХ и дисперсией DX. Над этой случайной величиной Х производится п независимых опытов, в результате которых она принимает значения Х1, Х2, ... , Хп (п “экземпляров” случайной величины Х). Пусть
Тогда последовательность 
сходится по вероятности к MX: 
Доказательство. Найдём MYn и DYn :
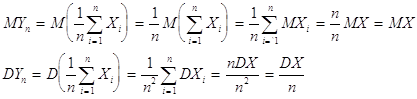
Применим к случайной величине Yn неравенство Чебышева, в котором положим a равным e, где e>0 — сколь угодно малое, наперёд заданное число.
Как бы ни было мало e, всегда можно выбрать n таким большим, чтобы правая часть последнего неравенства стала меньше сколь угодно малого положительного числа d; следовательно, при достаточно большом п
P{|Yn-MX|³e}<d
ÞP{|Yn-MX|<e}>1-d,
а это равносильно сходимости по вероятности Yn к MX
Замечание 1.5.1. Первую теорему Чебышева можно записать и иначе, если положить Zn:=Yn-MX
Замечание 1.5.2. Первая теорема Чебышева относится к случаю, когда случайные величины Х1, Х2, ... , Хп независимы и имеют одно и то же распределение, а значит одно и то же MX и DX.
Рассмотрим случай, когда условия производимых опытов меняются.
Вторая теорема Чебышева. Пусть имеется случайная величина Х. Над ней производятся независимые опыты, в результате чего мы получаем последовательность
Х1, Х2, ..., Хn, ...
с различными, в общем случае, MХi и DXi (i=
). Пусть
Если DXi£D i=1, 2, ... , где D - некоторое положительное число, то
Доказательство.
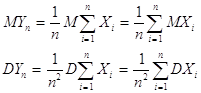(1.5.1)
Согласно неравенства Чебышева
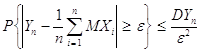
или, учитывая (1.5.1), имеем
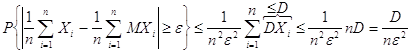
Как бы ни было мало произвольное наперёд заданное e, всегда можно выбрать n таким большим, чтобы правая часть последнего неравенства стала меньше произвольно малого d. Следовательно
,
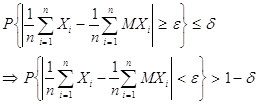что и требовалось доказать.
Замечание 1.5.3. При формулировке второй теоремы Чебышева нельзя говорить, что
так как 
зависят от n, а понятие “сходимость по вероятности” определено нами только для постоянной а, не зависящей от n.
Похожие работы
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... по соответствующему полю). В окне Конструктора таблиц созданные связи отображаются визуально, их легко изменить, установить новые, удалить (клавиша Del). 1 Многозвенные информационные системы. Модель распределённого приложения БД называется многозвенной и её наиболее простой вариант – трёхзвенное распределённое приложение. Тремя частями такого приложения являются: ...
... , вторая в среднем убывает. 3. D(x±h)=D(x)+D(h)±2mxh Доказательство. D(x±h)=M((x±h)2)—M2(x±h)=M(x2±2xh+h2)—(M(x)±M(h))2=M(x2)±2M(xh)+M(h2)—+M2(x)+2M(x)*M(h)—M2(h)=D(x)+D(h)±2(M(xh))—M(x)*M(h)=D(x)+D(h)±2mxh Вопрос 31 Мат. статистика опирается на теорию вероятностей, и ее цель – оценить характеристики генеральной совокупности по выборочным данным. Генеральной совокупностью называется ...
... поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
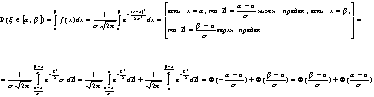
0 комментариев