Навигация
Доверительная оценка при неизвестной вероятности по большим выборкам
1.1.1 Доверительная оценка при неизвестной вероятности по большим выборкам
Частота ![]() является точечной оценкой
является точечной оценкой ![]() , она асимптотически нормально распределена с
, она асимптотически нормально распределена с ![]() и
и 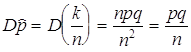 .
.
Если ![]() ,то
,то ![]() . Зададим
. Зададим ![]() . Величина
. Величина ![]() такая, что
такая, что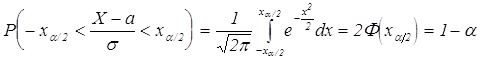 может быть найдена из уравнения
может быть найдена из уравнения ![]() при помощи таблиц для функций Лапласа. Эти же рассуждения применим к
при помощи таблиц для функций Лапласа. Эти же рассуждения применим к ![]() . По заданному
. По заданному ![]() можно найти
можно найти ![]() так, чтобы
так, чтобы 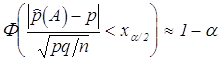 . Из неравенства
. Из неравенства 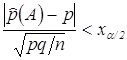 следует, что
следует, что 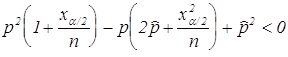 , откуда можно вычислить оба значения
, откуда можно вычислить оба значения ![]() и
и ![]() , которые представляют доверительные оценки для
, которые представляют доверительные оценки для ![]() . Если
. Если ![]() выбрано достаточно малым, то случайный интервал
выбрано достаточно малым, то случайный интервал ![]() “покрывает”
“покрывает” ![]() почти наверное.
почти наверное.
1.1.2 Доверительные оценки для параметров нормального закона
1.1.2.1 Доверительная оценка ![]() при известном
при известном ![]()
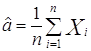 ,
,![]() , тогда
, тогда 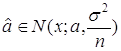 .
.
Соответственно,
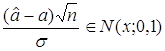 .
.
Для стандартной нормальной случайной величины с уровнем значимости ![]() нижняя и верхняя критические границы соответственно равны
нижняя и верхняя критические границы соответственно равны ![]() и
и ![]() .
.
Имеем
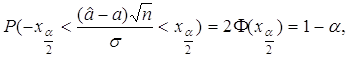 или
или
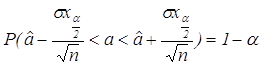 .
.
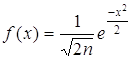 .
.
Таким образом, 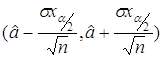 - доверительная оценка для параметра a с мерой надежности
- доверительная оценка для параметра a с мерой надежности ![]() .
.
1.1.2.2 Доверительная оценка ![]() при неизвестном
при неизвестном ![]()
Оценка основана на том факте, что при высказанных предположениях величина ![]() удовлетворяет t- распределению с n-1 степенями свободы.
удовлетворяет t- распределению с n-1 степенями свободы.
Определяя одностороннюю критическую точку ![]() из условия
из условия 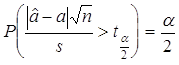 ,получим доверительную оценку для а в виде
,получим доверительную оценку для а в виде
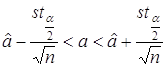 .
.
Для конкретной выборки ![]() объема n доверительная оценки для а становится ее доверительным интервалом.
объема n доверительная оценки для а становится ее доверительным интервалом.
1.1.2.3 Доверительная оценка![]() при неизвестном
при неизвестном ![]()
Отправной точкой является тот факт, что при заданных предпосылках величина ![]() удовлетворяет
удовлетворяет ![]() - распределению с n-1 степенями свободы. По заданному уровню значимости
- распределению с n-1 степенями свободы. По заданному уровню значимости ![]() и
и ![]() степенями свободы находим критические точки
степенями свободы находим критические точки ![]() и
и ![]() распределения
распределения ![]() такие, что
такие, что
![]() ,
, ![]()
![]() , или
, или 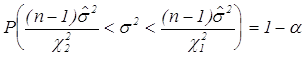 .
.
Таким образом , 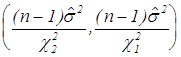 есть доверительная оценка
есть доверительная оценка ![]() с мерой надежности
с мерой надежности ![]() .
.
Похожие работы
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... по соответствующему полю). В окне Конструктора таблиц созданные связи отображаются визуально, их легко изменить, установить новые, удалить (клавиша Del). 1 Многозвенные информационные системы. Модель распределённого приложения БД называется многозвенной и её наиболее простой вариант – трёхзвенное распределённое приложение. Тремя частями такого приложения являются: ...
... , вторая в среднем убывает. 3. D(x±h)=D(x)+D(h)±2mxh Доказательство. D(x±h)=M((x±h)2)—M2(x±h)=M(x2±2xh+h2)—(M(x)±M(h))2=M(x2)±2M(xh)+M(h2)—+M2(x)+2M(x)*M(h)—M2(h)=D(x)+D(h)±2(M(xh))—M(x)*M(h)=D(x)+D(h)±2mxh Вопрос 31 Мат. статистика опирается на теорию вероятностей, и ее цель – оценить характеристики генеральной совокупности по выборочным данным. Генеральной совокупностью называется ...
... поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
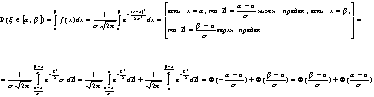



0 комментариев