Навигация
Понятие доверительного интервала
32759
знаков
4
таблицы
7
изображений
1.6 Понятие доверительного интервала
Будем считать, что независимая выборка 
взята из распределения, зависящего от скалярного параметра 
. Будем обозначать через 
распределение вероятностей, соответствующее значению 
неизвестного параметра.
Определение 1.6.1
-доверительным интервалом называется интервал вида 
где 
такой, что
Число называют доверительной вероятностью.
Другими словами, доверительный интервал обладает тем свойством, что, во-первых, его границы вычисляются исключительно по выборке (и, следовательно, не зависят от неизвестного параметра), и, во-вторых, он накрывает неизвестный параметр с вероятностью .
Значение доверительной вероятности 
выбирается заранее, этот выбор определяется конкретными практическими приложениями.
Смысл величины 
-- вероятность допустимой ошибки. Часто берут значения 
и т.п.
Ниже мы приводим один из методов построения доверительных интервалов. Он состоит из трех этапов.
1. Выбираем функцию 
, зависящую от выборки и от неизвестного параметра, такую, что ее функция распределения
не зависит от неизвестного параметра .
2. Выбираем два числа 
и 
таким образом, чтобы 
. Подбираем 
и 
, удовлетворяющие условиям
|
| (6.1) |
3. Таким образом,
|
| (6.2) |
причем и не зависят от .
4. Решим двойное неравенство 
относительно . В том случае, когда его решением является интервал, обозначим его левый и правый концы через 
и 
соответственно. Естественно, они зависят от выборки: 
, 
. В силу (6.2)
Следовательно, 
-- искомый -доверительный интервал.
Замечание 1.6.1
Описанная процедура, разумеется, не является универсальной. Во-первых, вопрос о выборе функции 
решается в каждом конкретном случае и по этому поводу нет общих рекомендаций. Во-вторых, совершенно не гарантировано, что решением неравенства в п. 3 будет интервал конечной длины. Вместе с тем, во многих важных случаях изложенный выше метод приводит к хорошим доверительным интервалам. Например, оправдано применение такого метода в случае, когда при каждой фиксированной выборке функция 
является строго монотонной и непрерывной по переменной .
Замечание 1.6.2
В силу неоднозначности выбора функции и чисел 
и 
, можно заключить, что -доверительный интервал неединственен.
Похожие работы
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... по соответствующему полю). В окне Конструктора таблиц созданные связи отображаются визуально, их легко изменить, установить новые, удалить (клавиша Del). 1 Многозвенные информационные системы. Модель распределённого приложения БД называется многозвенной и её наиболее простой вариант – трёхзвенное распределённое приложение. Тремя частями такого приложения являются: ...
... , вторая в среднем убывает. 3. D(x±h)=D(x)+D(h)±2mxh Доказательство. D(x±h)=M((x±h)2)—M2(x±h)=M(x2±2xh+h2)—(M(x)±M(h))2=M(x2)±2M(xh)+M(h2)—+M2(x)+2M(x)*M(h)—M2(h)=D(x)+D(h)±2(M(xh))—M(x)*M(h)=D(x)+D(h)±2mxh Вопрос 31 Мат. статистика опирается на теорию вероятностей, и ее цель – оценить характеристики генеральной совокупности по выборочным данным. Генеральной совокупностью называется ...
... поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
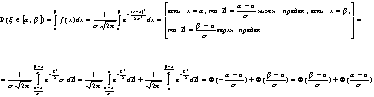
0 комментариев