Навигация
Метод наибольшего правдоподобия
32759
знаков
4
таблицы
7
изображений
1.2 Метод наибольшего правдоподобия
Пусть дана выборка 
объема n из генеральной совокупности с непрерывно распределенной случайной величиной X. Пусть плотность вероятности X содержит неизвестный параметр
, который следует оценить по выборке, и имеет вид 
.
Функцией правдоподобия называют функцию параметра , определяемую соотношением
. (1.2.1)
Рассмотрим случай дискретной случайной величины X с возможными значениями 
и вероятностями 
. Обозначим через 
наибольшее из возможных значений, которое встречается в выборке, а через 
— абсолютные частоты, с которыми появляются значения 
в выборке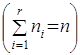 
. В этом случае функцией правдоподобия называют функцию параметра , определяемую соотношением
.
(1.2.2)
Метод наибольшего правдоподобия состоит в том, что в качестве оценки параметра берется значение, при котором функция правдоподобия достигает своего максимума.
Параметр находят, решая относительно уравнение
.
(1.2.3)
Часто вместо (1.2.3) используют уравнение
, 
(1.2.4)
Если плотность 
или вероятности 
зависят от 
параметров, то наиболее правдоподобную оценку системы параметров 
получают решением системы уравнений
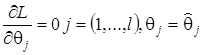(1.2.5)
или
.
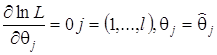(1.2.6)
Наиболее правдоподобные оценки имеют некоторые замечательные свойства. При достаточно общих условиях они являются состоятельными и асимптотически нормально распределенными (однако не всегда несмещенными), имеют среди всех асимптотически нормально распределенных оценок наибольшую эффективность. Справедливо следующее положение: если вообще имеется эффективная оценка, то она получается методом наибольшего правдоподобия.
Пример 1.2.1
Оценить вероятность 
некоторого события 
. Пусть
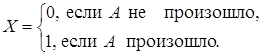
Решение. 
; 
. Пусть в 
независимых наблюдениях событие произошло 
раз, т.е. 
. Таким образом, имеем 
, 
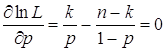. Отсюда следует, что 
. Следовательно, 
есть наиболее правдоподобная оценка параметра . Случайная величина k биномиально распределена, 
; 
Следовательно, 
— несмещенная оценка вероятности, асимптотически состоятельная и асимптотически нормальная.
Пример 1.2.2. Пусть случайная величина 
распределена по закону Пуассона с неизвестным параметром 
. Проведем выборку и получим значения 
( 
– целые числа). Пусть 
– набольшее из наблюдаемых в выборке чисел, 
– абсолютные частоты, с которыми числа 
появляются в выборке ;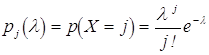 
. Тогда согласно формуле (3.2) 
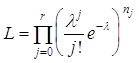. Из соотношения получаем 
, откуда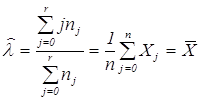 
.
Величина 
есть, таким образом, правдоподобная оценка для и вместе с тем состоятельная, асимптотически нормально распределенная.
Пример 1.2.3. Пусть случайная величина распределена нормально с параметрами 
и 
. Их следует оценить исходя их выборки объема 
.
Решение. Функция правдоподобия
,
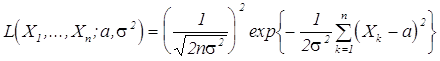следовательно
.
Согласно (2.5), получаем следующие уравнения для определения и : 
; 
, откуда 
и 
. Следовательно, 
есть наиболее правдоподобная оценка параметров 
. Мы уже знаем, что 
не является несмещенной оценкой, а только асимптотически не смещена.
Похожие работы
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... по соответствующему полю). В окне Конструктора таблиц созданные связи отображаются визуально, их легко изменить, установить новые, удалить (клавиша Del). 1 Многозвенные информационные системы. Модель распределённого приложения БД называется многозвенной и её наиболее простой вариант – трёхзвенное распределённое приложение. Тремя частями такого приложения являются: ...
... , вторая в среднем убывает. 3. D(x±h)=D(x)+D(h)±2mxh Доказательство. D(x±h)=M((x±h)2)—M2(x±h)=M(x2±2xh+h2)—(M(x)±M(h))2=M(x2)±2M(xh)+M(h2)—+M2(x)+2M(x)*M(h)—M2(h)=D(x)+D(h)±2(M(xh))—M(x)*M(h)=D(x)+D(h)±2mxh Вопрос 31 Мат. статистика опирается на теорию вероятностей, и ее цель – оценить характеристики генеральной совокупности по выборочным данным. Генеральной совокупностью называется ...
... поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
0 комментариев