Навигация
1.2.2 Умножение матриц
Произведение С = А×В может быть получено тогда и только тогда, когда число столбцов матрицы А равно числу строк матрицы В.
Если А размера m´t и В размера t´n, то матрица С = А×В определяется формулой
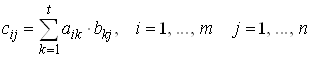 . (1.10)
. (1.10)
Заметим, что в общем случае А×В ≠ В×А.
Если А×В=В×А, то матрицы коммутирующие или перестановочные.
Умножение обладает свойствами:
А×(В×С) = (А×В) ×С (1.11)
ассоциативности и
(А+В) ×С=А×С+В×С и А×(В+С)=А×В+А×С (1.12)
дистрибутивности.
1.2.3 Умножение на скаляр
Умножение матрицы (А) на скаляр b означает, что каждый элемент матрицы умножается на скаляр
 (1.13)
(1.13)
1.2.4. Вычисление определителей
Пусть А – квадратная матрица порядка n, n>1:
 .
.
Определителем квадратной матрицы А порядка n, n>1 называется число
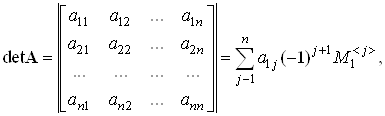
где ![]() – определитель квадратной матрицы порядка n-1, полученной из матрицы А вычеркиванием первой строки и j-того столбца.
– определитель квадратной матрицы порядка n-1, полученной из матрицы А вычеркиванием первой строки и j-того столбца.
Формулу 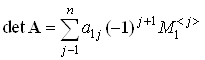 называют формулой вычисления определителя разложением по первой строке. Число
называют формулой вычисления определителя разложением по первой строке. Число ![]() называется алгебраическим дополнением элемента a1j.
называется алгебраическим дополнением элемента a1j.
1.2.5 Обращение матрицы
Если А и В-две квадратные матрицы порядка n, такие, что
А×В=Е, (1.14)
то говорят, что В-матрица, обратная к А, и обозначается через
В=А-1 ,(1.15)
заметим, что А×А-1=А-1×А=Е,
![]() (1.16)
(1.16)
где D=detА (определитель матрицы А); ![]() – алгебраическое дополнение элемента аij., а Мijминор к элементу aij (определитель, полученный из А удалением i-й строки и j-ого столбца.
– алгебраическое дополнение элемента аij., а Мijминор к элементу aij (определитель, полученный из А удалением i-й строки и j-ого столбца.
Обращение обладает свойствами:
![]() (1.17)
(1.17)
А-1 существует, если det A¹0.
Если det A=0, то матрица особенная.
1.3 Матричное представление линейных уравненийСистема линейных уравнений может быть записана в виде матричного уравнения:
А×Х=В. (1.18)
Ее решение получаем, умножая обе части равенства слева на А-1:
А-1×А×Х=1×Х=А-1×В,
то есть:
Х=А-1×В. (1.19)
Это удобный способ выразить решение Х, но существуют методы решения значительно лучше, чем явное формирование матрицы А-1 и умножение ее на В.
1.4 Используемые инструменты MathCAD
Большинство вычислений с матрицами, как и другие вычисления в Mathcad, можно выполнить тремя способами: с помощью панелей инструментов, выбором операции в меню или обращением к соответствующей функции.
Панель операций с матрицами и векторами в Matrix открывается щелчком по кнопке ![]() в панели математических инструментов. За кнопками панели закреплены следующие функции:
в панели математических инструментов. За кнопками панели закреплены следующие функции:
![]() – определение размеров матрицы;
– определение размеров матрицы;
![]() – ввод нижнего индекса;
– ввод нижнего индекса;
![]() – вычисление обратной матрицы;
– вычисление обратной матрицы;
![]() – вычисление определителя матрицы:
– вычисление определителя матрицы: ![]() ;
;
вычисление длины вектора |х|, |х|2=![]() ;
;
![]() – поэлементные операции с матрицами: если А={аij}, B={bij}, то
– поэлементные операции с матрицами: если А={аij}, B={bij}, то ![]() ;
;
![]() – определение столбца матрицы: М<j> – j-й столбец матрицы;
– определение столбца матрицы: М<j> – j-й столбец матрицы;
![]() – транспонирование матрицы: М={mij}, MT={mji},
– транспонирование матрицы: М={mij}, MT={mji},
![]() – вычисление скалярного произведения векторов:
– вычисление скалярного произведения векторов: 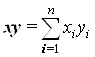 ;
;
![]() – вычисление векторного произведения двух векторов: a´b=(a2b2 – a3b2 – a2b1 – a1b2 – a2b1);
– вычисление векторного произведения двух векторов: a´b=(a2b2 – a3b2 – a2b1 – a1b2 – a2b1);
![]() – вычисление суммы компонент вектора:
– вычисление суммы компонент вектора: 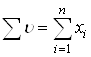 ;
;
![]() – определение диапазона изменения индекса переменной;
– определение диапазона изменения индекса переменной;
![]() – визуализация цифровой информации, сохраненной в матрице.
– визуализация цифровой информации, сохраненной в матрице.
Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно выделить матрицу и щелкнуть в панели по кнопке операции либо щелкнуть по кнопке в панели и ввести в помеченной позиции для матрицы.
Функции определения матриц и операции с блоками матриц:
matrix (m, n, f) – создает и заполняет матрицу размерности m´n, элемент которой, расположенный в i-й строке, j-м столбце, равен значению f (i, j) функции f (x, y);
diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
identity(n) – создает единичную матрицу порядка n;
augment (A, B) – формирует матрицу, в первых столбцах которой содержится матрица А, а в последних – матрица В (матрицы А и В должны иметь одинаковое число строк);
staсk (А, В) – формирует матрицу, в первых строках которой содержится матрица А, а в последних – матрица В (матрицы А и В должны иметь одинаковое число столбцов);
submatrix (A, ir, jr, ic, jc) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с ir по jr и в столбцах с ic по jc, ir£jr, ic£jc.
Номер первой строки (столбца) матрицы или первой компоненты вектора хранится в Mathcad в переменной ORIGIN. По умолчанию в Mathcad координаты векторов, столбцы и строки матрицы нумеруются, начиная с 0 (ORIGIN=0). Поскольку в математической записи чаще используется нумерация с 1, здесь и в дальнейшем перед началом работы с матрицами будем определять значение переменной ORIGIN равным 1, т.е. будем прежде всего выполнять команду ORIGIN=1.
Функции вычисления числовых характеристик матриц:
last(v) – вычисление номера последней компоненты вектора v;
legth(v) – вычисление количества компонент вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице А;
min(A) – вычисление наименьшего элемента в матрице А;
tr(A) – вычисление следа квадратной матрицы А*;
rank(A) – вычисление ранга матрицы А;
norm1 (A), norm2 (A), norme(A), normi(A) – вычисление норм квадратной матрицы А.
Функции, реализующие численные алгоритмы решения задач линейной алгебры:
rref(A) – приведение матрицы к ступенчатому виду с единичным базисным минором (выполняет элементарные операции со строками матрицы);
eigenvals(A) – вычисление собственных значений квадратной матрицы А;
eigenvecs(A) – вычисление собственных векторов квадратной матрицы А; значением функции является матрица, столбцы которой есть собственные векторы матрицы А, порядок следования которых отвечает порядку следования собственных значений, вычисленных функцией eigenvals(A);
eigenvec (A, l) – вычисление собственного вектора матрицы А, отвечающего собственному значению l;
lsolve (A, b) – решение системы линейных уравнений Ax=b.
Задание 1. Определить матрицу А размером 3´3 с помощью панели Matrix и трансформировать ее.
Создать матрицу В размером 3´3 с помощью функции Matrix.
Вычислить суммы А+В и В+А, произведения АВ и ВА, исследовать матрицы на симметричность.
Задать единичную матрицу Е 3-го порядка, вычислить произведения ЕА и АЕ.
Сформировать вектор v, представляющий 2-й столбец матрицы А, и диагональную матрицу diag(v).
Определить матрицы С и D, используя функции augment (A, V) и staсk (A, VT).
Решить систему АХ=V, используя обратную матрицу А-1 и функцию isolve (A, b).
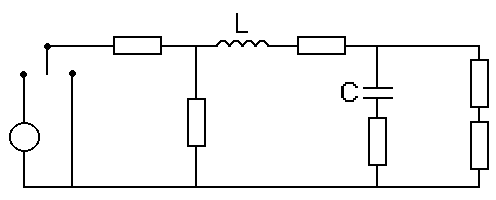
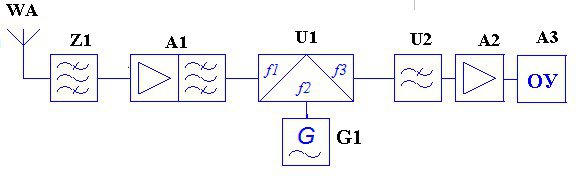
2. Основные элементы схемы и понятия
Похожие работы
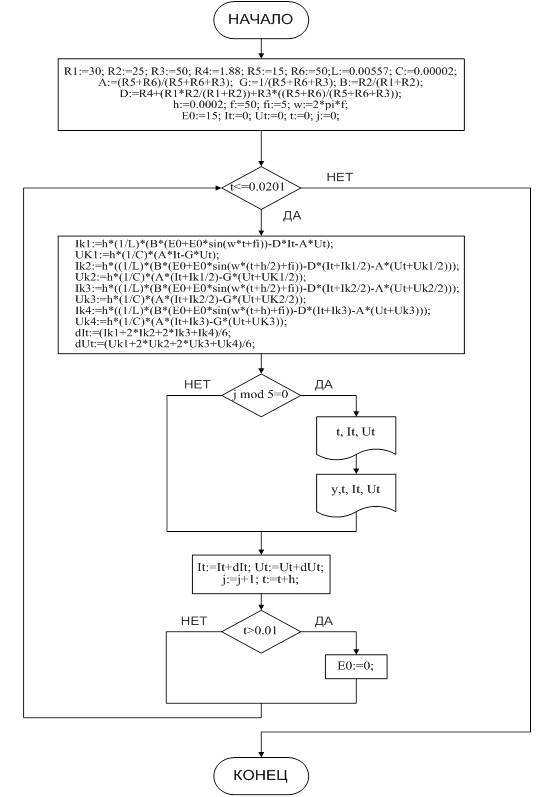
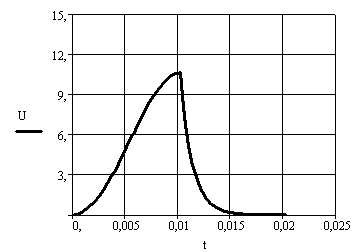
... колебаний Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Гц - линейная частота с. - текущее время с. - текущее время Рад - фаза 1.3 Описание работы электрической цепи В начальный момент времени ключ находится в положении . При этом цепь разомкнута, напряжение на конденсаторе и ток на катушке равны нулю . Происходит первое переключение ключа, ...
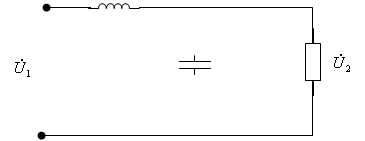
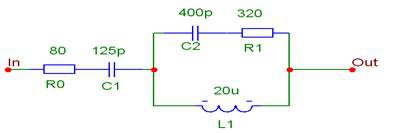
... хода 4х-П представляет собой частный случай входного сопротивления (1.5) при Сопротивление короткого замыкания получается из (1.5) при 1.4 Передаточная функция четырехполюсника При проектировании радиотехнических устройств широко применяются электрические фильтры, которые удобно рассматривать как 4х-П, предназначенные для передачи сигналов от входа к выходу с определенной ...
... - в группе переменных, «зажатых в кулак», но этот «кулак», как мы уже отмечали, легко разжать, выводя на дисплей найденные значения с «первородной» размерностью массы (kg), длины (m) и времени (sec): пакет MathCAD «разжимает» и сам вектор, м составные размерности, приписывая к числам комбинации основных физических единиц. Но не только этим хороша размерность в задачах. Главное то , что она ...
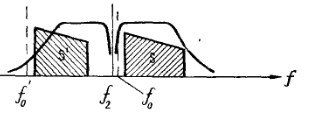
... полезных сигналов, а также динамический диапазон сигналов на выводе РПрУ не должно превышать 10 дБ. 4 Анализ и моделирование структуры РПУ Так как для общих характеристик радиоприемного устройства исходными данными для расчета являются не только диапазон рабочих частот, но и параметры приемной антенны, такие как емкость, индуктивность, активное сопротивлении и тд. Следовательно будем ...
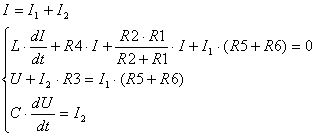





0 комментариев