Навигация
3.4 Узловые уравнения
Для формирования системы уравнений относительно узловых напряжений выразим ![]() через параметры пассивных и активных элементов обобщенных ветвей:
через параметры пассивных и активных элементов обобщенных ветвей:
![]() .
.
Согласно первому закону Кирхгофа, для узлов графа
AI=-AJ или AYU=-AJ.
Теперь напряжение на ветвях определим через узловые потенциалы:
U=AT×j+Е.
Таким образом, получаются уравнения
AY×AT×j=AJ-AY×E, (3.14)
которые называют узловыми уравнениями.
Если ввести обозначения
– Yy=AY×AT – матрица узловых проводимостей,
– Jy=AJ-AY×E – матрица узловых токов,
то узловые уравнения запишутся кратко:
Yy j=Jy.(3.14a)
При выполнении узлового анализа на ЭВМ обычно не строятся матрицы A и Y и не выполняют матричные умножения, а непосредственно пользуются правилами составления узловых уравнений:
1. Диагональные элементы матрицы Yу положительны и Yjj равны сумме проводимостей ветвей, подключенных к j-му узлу.
2. Внедиагональные элементы матрицы Yy отрицательны и Yjk равны сумме проводимостей ветвей, включенных между j-м и k-м узлами.
3. Произвольный элемент вектора тока Jy с номером j Jj равны сумме узловых токов, втекающих в j-узел.
Тогда l-я ветвь, направленная от узла j к узлу k, приводит к следующему вкладу в матрицы Yy и Jy:
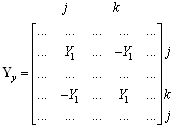
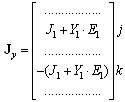
Так составляются уравнения по методу узловых потенциалов последовательным перебором топологического списка ветвей схемы.
Потенциалы узлов jkравны напряжениям Vk между q-1 узлом и опорным узлом.
3.5 Контурные уравнения
Уравнения на основе второго закона Кирхгофа
CU=CE,
уравнение закона Ома
U=Z×I
и соотношение
![]()
подставим в контурное уравнение и получим:
![]() .
.
Токи в обобщенных ветвях определим через контурные токи:
![]() .
.
Так получаются контурные уравнения:
![]() . (3.15)
. (3.15)
Если ввести обозначения
Zk=СZ×СT – матрица контурных сопротивлений,
Ek= СE-СZ×J – матрица контурных ЭДС, то контурные уравнения запишутся в виде:
![]() . (3.15а)
. (3.15а)
В матричной форме решения для контурных токов
![]() (3.16)
(3.16)
выражают принцип наложения.
3.6 Независимые токи и напряжения
Запишем уравнения ЗКТ, используя матрицу главных сечений:
D×I=0,
где I – вектор токов ветвей.
Разделив матрицу на блоки, получим: 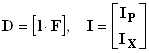

или
IP= – F×IX.(3.17)
Токи ребер графа выражаются через токи хорд:
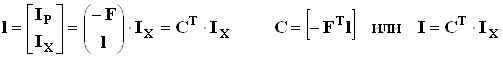 (3.17а)
(3.17а)
Токи хорд можно рассматривать как независимые переменные.
Уравнения, составленные по ЗКН,
CU=0,
где U – вектор напряжений на всех ветвях, использовав блочное представление матрицы С, запишем:
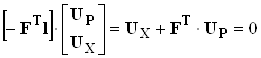 .
.
Напряжение на ветвях хорд выражаются через напряжения на ветвях ребер:
UX=FT×UP. (3.18)
Напряжение на ветвях можно представить:
 .
.
Из последнего, с учетом D=[l×F], следует:
U = DT×UP. (3.18а)
Напряжения, соответствующие ребрам графа, можно рассматривать как независимые переменные.
3.7 Типы ветвей
Y-ветвью называют ветвь, представленную проводимостью и описываемую компонентными уравнениями для токов. Ветвь включает проводимости, ветвь ИТУН, ветвь ИТУТ, независимые источники тока (рис. 3.10).
![]() ,
,
где ![]()
![]() - коэффициент передачи по току;
- коэффициент передачи по току;
gij – передаточная проводимость.
В матричной форме уравнения для Y ветвей:
![]() . (3.19)
. (3.19)
В матрицу проводимостей Y включены проводимости ветвей и и передаточные проводимости. К этим уравнениям присоединяются уравнения многополюсников в Y-форме.
IM=YM×UM.
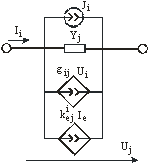
Рис. 3.10.
Z-ветви характеризуются сопротивлениями и описываются напряжениями.
Обобщенная 2-полюсная Z-ветвь показана на рис. 3.11:
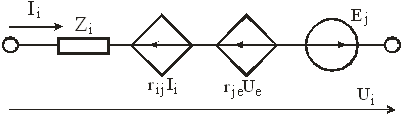
Рис. 3.11.
![]() ,
,
где rji – передаточное сопротивление;
![]() – коэффициент передачи по напряжению.
– коэффициент передачи по напряжению.
Уравнение Z-ветвей в матричной форме имеет вид:
UZ=Z×IZ+KU×UY-E. (3.20)
В Z матрицу входят сопротивления ветвей и передаточные сопротивления. Уравнения Z-ветвей дополняются уравнениями многополюсников в Z-форме.
UM=ZM×IM
Компонентные уравнения обобщенных ветвей:
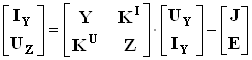 . (3.21)
. (3.21)
Похожие работы
... колебаний Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Гц - линейная частота с. - текущее время с. - текущее время Рад - фаза 1.3 Описание работы электрической цепи В начальный момент времени ключ находится в положении . При этом цепь разомкнута, напряжение на конденсаторе и ток на катушке равны нулю . Происходит первое переключение ключа, ...
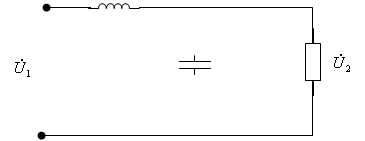
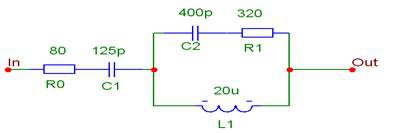
... хода 4х-П представляет собой частный случай входного сопротивления (1.5) при Сопротивление короткого замыкания получается из (1.5) при 1.4 Передаточная функция четырехполюсника При проектировании радиотехнических устройств широко применяются электрические фильтры, которые удобно рассматривать как 4х-П, предназначенные для передачи сигналов от входа к выходу с определенной ...
... - в группе переменных, «зажатых в кулак», но этот «кулак», как мы уже отмечали, легко разжать, выводя на дисплей найденные значения с «первородной» размерностью массы (kg), длины (m) и времени (sec): пакет MathCAD «разжимает» и сам вектор, м составные размерности, приписывая к числам комбинации основных физических единиц. Но не только этим хороша размерность в задачах. Главное то , что она ...
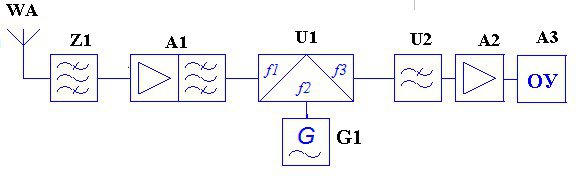
... полезных сигналов, а также динамический диапазон сигналов на выводе РПрУ не должно превышать 10 дБ. 4 Анализ и моделирование структуры РПУ Так как для общих характеристик радиоприемного устройства исходными данными для расчета являются не только диапазон рабочих частот, но и параметры приемной антенны, такие как емкость, индуктивность, активное сопротивлении и тд. Следовательно будем ...
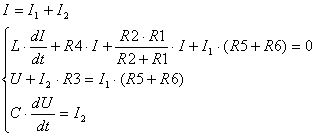





0 комментариев