Навигация
3.2.3 Матрица контуров
Матрица контуров С – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа (ЗКН). Строки матрицы С соответствуют контурам, столбцы – ветвям.
Элементы сij матрицы С=[сij] определяются следующим образом:
сij=1, если ветвь j содержится в контуре i и направление ветви совпадает с направлением обхода контура;
сij=-1, если ветвь j содержится в контуре i и направление ветви противоположно направлению обхода контура;
сij= 0, если ветвь j не содержится в контуре i.
Матрицу С, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура.
Второй закон Кирхгофа для напряжений в матричной форме записывают следующим образом (ЗКН):
(3.6)
Токи всех обобщенных ветвей могут быть выражены как линейные комбинации токов обобщенных ветвей связи (контурных токов)
(3.7)
где IК – столбовая матрица контурных токов.
Если ветвям дерева присвоены первые номера, то матрица главных контуров состоит из двух подматриц:
(3.8)
где F – подматрица матрицы сечений C, составленная на основании того же самого дерева;
1 – единичная подматрица порядка k=р-q+l.
Таким образом, в матричной форме могут быть записаны:
– первый закон Кирхгофа (ЗКТ):
(3.9)
– второй закон Кирхгофа (ЗКН):
3.3 Полная система уравнений электрических цепей
Законы Кирхгофа применительно к графу схемы или электрической цепи характеризуют систему в целом без учета характеристик ее элементов. Матричные уравнения
Ai=-AÁ (или Di=-DÁ) и Cu=Ce (3.10)
определяют систему из р отдельных уравнений. Такая система недостаточна для описания процессов в электрических цепях, так как не известны р токов и р напряжений.
Чтобы дополнить систему уравнений, необходимо определить (или задать) еще р уравнений. Эти уравнения должны отражать свойства элементов системы – ветвей электрической цепи. Очевидно, что такие связи должны быть записаны для р ветвей цепи. В матричной форме запишем эти уравнения в виде
i=f(u) или u=j(i),
т.е.
(3.11)
В зависимости от характера функций fk и jk (k=1…р) системы уравнений электрических цепей могут быть линейными – для линейных электрических цепей, т.е. для цепей, у которых r, L, С и М не зависят от значений и направлений токов и напряжений в цепи, и нелинейными – для нелинейных электрических цепей, т.е. для цепей, у которых r, L, С или М хотя бы одного из участков зависят от значений или от направлений токов и напряжений в этом участке цепи.
Каждая ветвь линейной цепи может содержать сопротивление, индуктивность, емкость, идеальный источник ЭДС и идеальный источник тока (рис. 3.9).
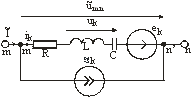
Рис. 3.9
Ток в сопротивлении ветви 
и падение напряжения ветви U связаны законом Ома.
U=Z×I,
где сопротивление ветви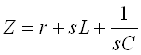 
. Эти соотношения для всех ветвей можно записать в матричной форме:
или кратко
U=Z×I, (3.12)
где Z – диагональная матрица сопротивлений ветвей;
U, I, J, E – соответственно векторы напряжений и токов ветвей, токов источников тока и ЭДС ветвей.
Это матричная форма закона Ома.
Замечание: Матрица Z диагональна лишь в случае, когда ток k-ой ветви создает напряжение на сопротивлении Z, k-ой ветви. В цепях со взаимной индукцией Z имеет элементы вне главной диагонали Zij=Zji=±sMij.
М-сопротивления индуктивной связи i-ой и j-ой ветвей. Они положительны (отрицательны), если ориентация i-ой и j-ой ветвей по отношению одноименных зажимов одинакова (противоположна).
Уравнения закона Ома можно представить в другой форме:
I=Y×U, (3.13)
где Y=Z-1 – матрица проводимостей, обратная матрице сопротивлений ветвей.
Если в функции fk и jk входят производные токов и напряжений, то процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных дифференциальных уравнений. При отсутствии производных в функциях fk и jk процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных алгебраических уравнений.
Система из 2 р уравнений, включающая в себя уравнения, записанные согласно законам Кирхгофа, и уравнения, характеризующие связи между токами и напряжениями элементов электрической цепи, и есть полная система уравнений электрической цепи, или полная математическая модель этой цепи.
Похожие работы
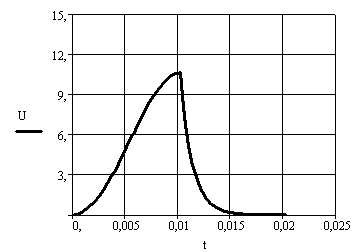
... колебаний Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Гц - линейная частота с. - текущее время с. - текущее время Рад - фаза 1.3 Описание работы электрической цепи В начальный момент времени ключ находится в положении . При этом цепь разомкнута, напряжение на конденсаторе и ток на катушке равны нулю . Происходит первое переключение ключа, ...
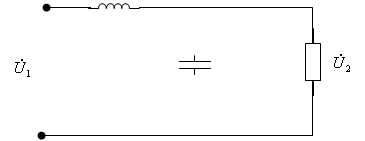
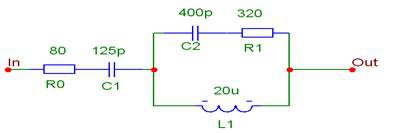
... хода 4х-П представляет собой частный случай входного сопротивления (1.5) при Сопротивление короткого замыкания получается из (1.5) при 1.4 Передаточная функция четырехполюсника При проектировании радиотехнических устройств широко применяются электрические фильтры, которые удобно рассматривать как 4х-П, предназначенные для передачи сигналов от входа к выходу с определенной ...
... - в группе переменных, «зажатых в кулак», но этот «кулак», как мы уже отмечали, легко разжать, выводя на дисплей найденные значения с «первородной» размерностью массы (kg), длины (m) и времени (sec): пакет MathCAD «разжимает» и сам вектор, м составные размерности, приписывая к числам комбинации основных физических единиц. Но не только этим хороша размерность в задачах. Главное то , что она ...
... полезных сигналов, а также динамический диапазон сигналов на выводе РПрУ не должно превышать 10 дБ. 4 Анализ и моделирование структуры РПУ Так как для общих характеристик радиоприемного устройства исходными данными для расчета являются не только диапазон рабочих частот, но и параметры приемной антенны, такие как емкость, индуктивность, активное сопротивлении и тд. Следовательно будем ...
0 комментариев