Навигация
Формирование уравнений цепи на основе теории графов
3. Формирование уравнений цепи на основе теории графов
3.1 Граф схемы и некоторые его подграфы
При разработке машинных методов анализа электрических цепей можно определить некоторые их свойства, рассматривая только структуры цепи. Теория графов является для этого удобным средством.
Для описания топологии (структуры) цепи заменим каждую ветвь схемы отрезком линии, называемым ветвью графа, а узлы точками – узлами (вершинами) графа.
Эта совокупность ветвей и узлов, представляющая топологию цепи, называется графом.
Графы называют изоморфными, если их топологические свойства одинаковы.
Графы, у которых все ветви ориентированы, называют ориентированными. В противном случае граф считают неориентированным. Планарным называют граф, который в результате изоморфных преобразований может быть изображен на плоскости без пересечения ветвей. Планарной электрической схеме соответствует планарный граф. На рис. 3.1 показана схема электрической цепи (а) и ее ориентированный граф (б):
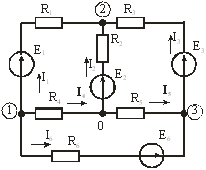
(а) (б)
Рис. 3.1
Подграфом графа называют часть графа. Подграфом может быть одна ветвь, узел или множество ветвей и узлов, содержащееся в данном графе.
Путь – упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются в этом пути только один раз (4–2–3).
Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути (1–2–4). На рис. 3.1 один из контуров содержит ветви 1, 2, 4.
Если между любой парой узлов графа существует путь, то граф называют связным.
Деревом связного графа называют связный подграф, содержащий все узлы графа, но не содержащий ни одного контура.
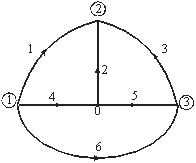
Примеры деревьев графа на рис. 3.1, б приведены на рис. 3.2:
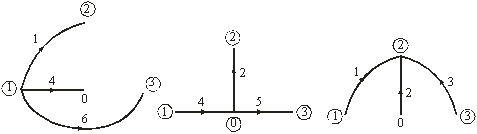
Рис. 3.2
Ветви графа, которые дополняют дерево до исходного графа, называют ветвями связи (хордами). Ветви графа, входящие в дерево, называют ребрами. Если граф содержит р ветвей и q узлов, то число ветвей любого дерева d=q-1, а число ветвей связи k=p-q+1.
Ветви связи деревьев графа на рис. 3.1, б приведены на рис. 3.3: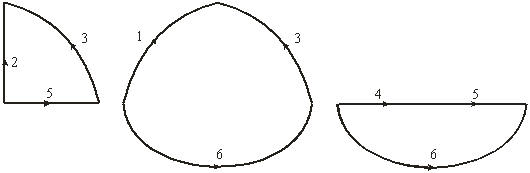
Рис. 3.3
Сечением графа называют множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых в частном случае может быть изолированным узлом.
Например, ветви графа 1–4–6, 3–2–4–6, 3–5–6 образуют сечения (рис. 3.4):
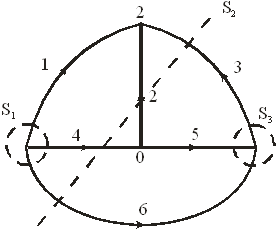
Рис. 3.4
Главным контуром называют контур, состоящий из ветвей дерева и только одной ветви связи. Другими словами, при соединении любой ветви связи с деревом образуется главный контур. Главным сечением считается сечение, состоящее из ветвей связи и только одной ветви дерева. Каждая ветвь дерева позволяет образовать одно сечение.
На рис. 3.5 показаны главные сечения, главные контуры для выделенного дерева графа (рис. 3.1, б):
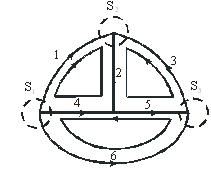
Рис. 3.5
3.2 Топологические матрицы графа
3.2.1 Матрица соединений
Матрица соединений (инциденций) А – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа (ЗКТ) для узлов.
Строки этой матрицы соответствуют узлам, столбцы – ветвям. Элементы аij матрицы А определяются следующим образом:
aij=1, если ветвь j соединена с узлом i и направлена от узла;
aij=-1, если ветвь j соединена с узлом i и направлена к узлу;
aij=0, если ветвь j не соединена с узлом i.
Число строк матрицы А равно числу независимых узлов g=q-1.
3.2.2 Матрица сечений
Матрица сечений D – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа (ЗКТ) для сечений. Строки матрицы D соответствуют сечениям, столбцы – ветвям.
Элемент dij матрицы D=[dij] определяется следующим образом:
dij=1, если ветвь j содержится в сечении i и направлена согласно с направлением сечения;
dij=-1, если ветвь j содержится в сечении i и направлена противоположно направлению сечения;
dij= 0, если ветвь j не содержится в сечении i.
Если матрица D составлена для главных сечений, то ее называют матрицей главных сечений. При этом за положительное направление сечения обычно принимают направление ветви дерева данного сечения. Число строк матрицы D равно числу независимых сечений g.
Закон Кирхгофа для сечений в матричной форме записывают следующим образом (ЗКТ):
![]() (3.3)
(3.3)
Если матрицу напряжений ветвей дерева (ребер) обозначить через Ug, то
![]() , (3.4)
, (3.4)
т.е. напряжения ветвей схемы, определяют через напряжения ветвей дерева (ребер).
Если ветвям дерева присвоены первые номера, то матрица главных сечений может быть разложена на две подматрицы:
D=[1 F], (3.5)
где 1 – единичная подматрица порядка q-1, столбцы которой соответствуют ребрам;
F – подматрица, столбцы которой соответствуют ветвям связи (хордам).
Похожие работы
... колебаний Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Гц - линейная частота с. - текущее время с. - текущее время Рад - фаза 1.3 Описание работы электрической цепи В начальный момент времени ключ находится в положении . При этом цепь разомкнута, напряжение на конденсаторе и ток на катушке равны нулю . Происходит первое переключение ключа, ...
... хода 4х-П представляет собой частный случай входного сопротивления (1.5) при Сопротивление короткого замыкания получается из (1.5) при 1.4 Передаточная функция четырехполюсника При проектировании радиотехнических устройств широко применяются электрические фильтры, которые удобно рассматривать как 4х-П, предназначенные для передачи сигналов от входа к выходу с определенной ...
... - в группе переменных, «зажатых в кулак», но этот «кулак», как мы уже отмечали, легко разжать, выводя на дисплей найденные значения с «первородной» размерностью массы (kg), длины (m) и времени (sec): пакет MathCAD «разжимает» и сам вектор, м составные размерности, приписывая к числам комбинации основных физических единиц. Но не только этим хороша размерность в задачах. Главное то , что она ...
... полезных сигналов, а также динамический диапазон сигналов на выводе РПрУ не должно превышать 10 дБ. 4 Анализ и моделирование структуры РПУ Так как для общих характеристик радиоприемного устройства исходными данными для расчета являются не только диапазон рабочих частот, но и параметры приемной антенны, такие как емкость, индуктивность, активное сопротивлении и тд. Следовательно будем ...





0 комментариев