Сеточная область

1.1 Сеточная область

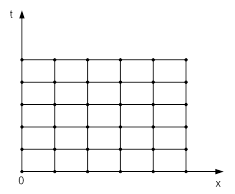
Для построения разностной схемы необходимо построить сетку G_h-конечное множество точек, принадлежащих G, плотность распределения которых характеризуется параметрами h-шагом сетки. Пусть область изменения аргумента x есть отрезок G={0≤x≤1}. Разобьем этот отрезок точками x_i=i∙h, i=0,n на n равных частей длины h=1/n каждая. Множество точек x_i=i∙h, называется равномерной сеткой на отрезке 0≤x≤1 и обозначим ={x_i=i∙h, i=0,n} , а число h-расстояние между точками (узлами) сетки называется шагом сетки. Разбиение отрезка 0≤x≤1 точками x_i, i=0,n можно производить произвольным образом - 0<x₁<…<x_n-1<1. Тогда получаем сетку ={x_i, i=0,n, x₀=0, x_n=1} c шагами h_i=x_i-x_i-1, которое зависит от номера узла сетки. Если h_i≠h_i+1 хотя бы в одной точке, то сетка называется неравномерной и такую сетку обозначают ŵ. Точки x₀ и x_n назовем граничными узлами и обозначим их г_h. Остальные узлы назовем внутренними и обозначим их w_h. Узлы соседние с граничащими назовем приграничными. Тогда имеем

=w_hг_h.

1.2 Сеточная функция. Пространство сеточных функций. Нормы сеточных функций

Функция y=y(x_i) дискретного аргумента x_iназывается сеточной функцией, определенной на сетке . Сеточные функции можно рассматривать как функции целочисленного аргумента, являющегося номером узла сетки, т. е. y=y(x_i)=y(i). Далее мы будем писать y(x_i)=y_i.

Сеточная область w_h зависит от параметра h. При различных значениях параметра h имеем различные сеточные области. Поэтому и сеточные функции y_h(x) зависят от параметра h.

Функции u(x) непрерывного аргумента являются элементами функционального пространства H. Множество сеточных функций y_h(x) образует пространство H_h. Таким образом, в методе сеток пространство H, заменяется пространством H_h сеточных функций y_h(x).

Так как рассматривается множество сеток {w_h}, то мы получаем множество {H_h} пространств сеточных функций, определенных на {w_h}.

Пусть u(x) - решение исходной непрерывной задачи

Lu(x)=f(x), (1)

; y_h- решение разностной задачи, . Для теории приближенных вычислений представляет большой интерес оценка близости u(x) и y_h(x), но u(x) и y_h(x) являются элементами из различных пространств. Пространство H отображается на пространство H_h. Каждой функции  ставится в соответствие сеточная функция y_h(x), x w_h, так что y_h=P_hu H_h, где P_h- линейный оператор из H в H_h. Это соответствие можно осуществить различными способами, т. е. зависит от выбора оператора P_h. Теперь, имея сеточную функцию u_h, образуем разность y_h-u_h, которая является вектором пространства H_h. Близость y_h и u_h характеризуется числом y_h-u_hHh , где _Hh – норма на H_h.

Соответствие функций u(x) и u_h можно установить различными способами, например,

u_h=u(x), x  w_h.

В дальнейшем мы будем пользоваться этим способом соответствия.

В линейном пространстве H_h введем норму _Hh, которая является аналогом нормы _Н в исходном пространстве Н. Обычно принято выбирать норму в пространстве H_h так, чтобы при стремлении к нулю h она переходила в ту или иную норму функций, заданных на всем отрезке, т.е. чтобы выполнялось условие

_Hh=_H, (2)

где _Н- норма в пространстве функций, определенных на отрезке, которому принадлежит решение.

Условие (2) называют условием согласования в пространствах H_h и Н.

Рассмотрим простейшие типы норм в H_h для случая сеток

w_h={x_i=i∙h} на отрезке 0≤x≤1.

1. Норма _Hh=

удовлетворяет условию (2), если в качестве Н рассматривать пространство непрерывных функций с нормой

_H=, H=[a,b],

а сеточную функцию определять в виде (2), т.е.

y_h(x)=u_h(x), x  w_h

2. Норма _Hh=

удовлетворяют условию (2), если за Н принять пространство непрерывных функций с нормой

_H=u²(x)dx, H=C[a,b] ,

а сеточную функцию определять в виде

y_h=u_h(x), x  w_h.

Похожие работы

Методы оценки температурного состояния

Скачать

59485

4

20

... на первой  и последующих  итерациях равна: ; (3.22) . (3.23) Критерием завершения итерационного процесса является условие: ,(3.24) где  - заданная точность расчета [4]. 4. Методы оценки термонапряженного состояния 4.1 Физические основы возникновения термических напряжений При изменении температуры происходит объемное расширение или сжатие твердого тела. Неравномерный нагрев ...

Численное исследование движения системы "газовая струя – жидкость"

Скачать

36871

3

34

... диаметрах критического сечения представлены на рисунке 2.24 Рисунок 2.24 - Зависимость оптимальной высоты поднятия фурмы от давления при различных диаметрах критического сечения сопла Лаваля 3. Численное исследование движения жидкости Приведены уравнения Навье - Стокса установившегося осесимметричного движения несжимаемой вязкой жидкости в переменных функция тока - вихрь. Проведено ...

Методы численного моделирования МДП-структур

Скачать

11306

2

0

... системы на ЭВМ, а так же требование его экономичности обуславливают применение регулярных сеток, расположение узлов в которых подчиняется определённым закономерностям. В практике численного моделирования микроэлектронных структур примеяются как непрерывные прямоугольные (неравномерные), так и треугольные сетки (рис.2.). Треугольная сетка позволяет с меньшим количеством дополнительных узлов сгущать ...

Нейрокомпьютерные системы

Скачать

243425

1

0

... . Реакции узлов более высокого уровня менее зависят от позиции и более устойчивы к искажениям. Структура Неокогнитрон имеет иерархическую структуру, ориен­тированную на моделирование зрительной системы челове­ка. Он состоит из последовательности обрабатывающих слоев, организованных в иерархическую структуру (рис. 10.8). Входной образ подается на первый слой и передается через плоскости, ...