Навигация
Неявные схемы
2.3 Неявные схемы
В отличие от явной схемы неявные схемы используются для задачи (1) – (3) во всех случаях 1) p0>0, pN>0; 2) p0<0, pN<0; 3) p0>0, pN<0; 4) p0<0, pN>0.
Рассмотрим 2 различные разностные схемы:
1) Центрально- разностная схема.
2) Трехточечная схема с весом.
Все эти схемы решаются методом прогонки и все эти разностные уравнения, т.е. полученные при аппроксимации схемы, вернее, уравнения сводятся к виду:

![]() (4)
(4)
Коэффициенты Ai, Bi, Ciдолжны удовлетворять условиям:
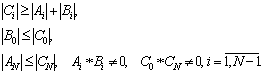 (5)
(5)
Коэффициенты B0 , C0 , F0, AN ,CN ,FN находятся из граничных условий. В данной задаче в зависимости от знака функции p(x,t) ставятся граничные условия и тем самым находятся наши коэффициенты. Рассмотрим все 4 случая:
1) p0>0, pN>0, u(l,t)=м2(t), (3′)
из уравнения (3′) ![]() AN ,CN ,FN .
AN ,CN ,FN .
B0 , C0 , F0 находятся из дополнительного условия, которая ставится на левом конце.
2) p0<0, pN<0, u(0,t)=м1(t), (3″) из уравнения (3″) ![]() B0 , C0 , F0.
B0 , C0 , F0.
AN ,CN ,FN находятся из дополнительного условия, которая ставится на правом конце.
3) p0<0, pN>0, u(0,t)=м1(t), u(l,t)=м2(t), (3″′)
из уравненя (3″′) ![]() B0 , C0 , F0
B0 , C0 , F0
![]() AN ,CN ,FN
AN ,CN ,FN
4) p0>0, pN<0, нет граничных условий.
Дополнительное условие ставится на левом и на правом концах. Находим B0, C0 , F0 , AN ,CN ,FN .
Алгоритм правой прогонки
![]()
![]() ,
, ![]() .
.
![]() ,
, ![]()
![]() .
.
При выполнении условий ![]() алгоритм правой прогонки устойчив.
алгоритм правой прогонки устойчив.
2.3.1 Центрально разностная схема
Разностная схема имеет вид (задачи (1)-(3)):
![]() ,
, ![]() .
.
![]()

1) P0>0, PN>0
![]()
![]() ,
, ![]() ,
, ![]() .
.

2) P0<0, PN<0
![]()
![]()
![]()
![]() .
.

3) P0<0, PN>0
![]() B0=0, C0=1, F0=
B0=0, C0=1, F0=![]() ,
,
![]() → AN=0, CN=1,
→ AN=0, CN=1, ![]() .
.
4) P0>0, PN<0
![]()
![]()
![]()
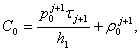
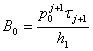 ,
, ![]()
![]()
![]()
![]()
Таблица 3. Численное решение уравнения переноса с переменными коэффициентами центральная разностная схема метод прогонки
| -------------kogda p0>0, pN>0------------ 50sloy | |||
| N priblijennoe tochnoe pogreshnosti | |||
| 0 | 0.18772094 | 0.18765555 | 0.00006539 |
| 1 | 0.18147920 | 0.18150347 | 0.00002427 |
| 2 | 0.17566576 | 0.17555308 | 0.00011268 |
| 3 | 0.16982701 | 0.16979776 | 0.00002924 |
| 4 | 0.16440069 | 0.16423113 | 0.00016956 |
| 5 | 0.15890974 | 0.15884699 | 0.00006275 |
| 6 | 0.15384782 | 0.15363937 | 0.00020845 |
| 7 | 0.14868453 | 0.14860247 | 0.00008206 |
| 8 | 0.14391438 | 0.14373070 | 0.00018368 |
| 9 | 0.13904086 | 0.13901865 | 0.00002221 |
| 10 | 0.13462315 | 0.13446108 | 0.00016208 |
| 11 | 0.13004378 | 0.13005292 | 0.00000914 |
| 12 | 0.12593278 | 0.12578928 | 0.00014351 |
| 13 | 0.12169429 | 0.12166541 | 0.00002888 |
| 14 | 0.11786577 | 0.11767675 | 0.00018903 |
| 15 | 0.11381884 | 0.11381884 | 0.00000000 |
Таблица 4. Численное решение уравнения переноса с переменными коэффициентами центральная разностная схема метод прогонки
| -------------kogda p0<0, pN<0-------------- 50sloy | |||
| N priblijennoe tochnoe pogreshnosti | |||
| 0 | 0.14715178 | 0.14715178 | 0.00000000 |
| 1 | 0.14240331 | 0.14232757 | 0.00007574 |
| 2 | 0.13769681 | 0.13766151 | 0.00003530 |
| 3 | 0.13325746 | 0.13314843 | 0.00010903 |
| 4 | 0.12885248 | 0.12878331 | 0.00006918 |
| 5 | 0.12470227 | 0.12456129 | 0.00014098 |
| 6 | 0.12057943 | 0.12047768 | 0.00010174 |
| 7 | 0.11669966 | 0.11652796 | 0.00017170 |
| 8 | 0.11284082 | 0.11270772 | 0.00013310 |
| 9 | 0.10921401 | 0.10901272 | 0.00020130 |
| 10 | 0.10560221 | 0.10543886 | 0.00016335 |
| 11 | 0.10221201 | 0.10198216 | 0.00022985 |
| 12 | 0.09883137 | 0.09863879 | 0.00019259 |
| 13 | 0.09566248 | 0.09540502 | 0.00025746 |
| 14 | 0.09249816 | 0.09227727 | 0.00022089 |
| 15 | 0.08953626 | 0.08925206 | 0.00028420 |
Таблица 5. Численное решение уравнения переноса с переменными коэффициентами центральная разностная схема метод прогонки
| -------------kogda p0<0, pN>0--------------50sloy | |||
| N priblijennoe tochnoe pogreshnosti | |||
| 0 | 0.03678794 | 0.03678794 | 0.00000000 |
| 1 | 0.03565917 | 0.03558189 | 0.00007728 |
| 2 | 0.03439784 | 0.03441538 | 0.00001754 |
| 3 | 0.03335557 | 0.03328711 | 0.00006846 |
| 4 | 0.03216179 | 0.03219583 | 0.00003404 |
| 5 | 0.03119895 | 0.03114032 | 0.00005863 |
| 6 | 0.03007027 | 0.03011942 | 0.00004915 |
| 7 | 0.02917987 | 0.02913199 | 0.00004788 |
| 8 | 0.02811435 | 0.02817693 | 0.00006258 |
| 9 | 0.02728957 | 0.02725318 | 0.00003639 |
| 10 | 0.02628567 | 0.02635971 | 0.00007405 |
| 11 | 0.02551993 | 0.02549554 | 0.00002439 |
| 12 | 0.02457633 | 0.02465970 | 0.00008337 |
| 13 | 0.02386341 | 0.02385126 | 0.00001215 |
| 14 | 0.02297890 | 0.02306932 | 0.00009042 |
| 15 | 0.02231302 | 0.02231302 | 0.00000000 |
Таблица 6. Численное решение уравнения переноса с переменными коэффициентами центральная разностная схема метод прогонки
| -------------kogda p0>0, pN<0--------------50sloy | |||
| N priblijennoe tochnoe pogreshnosti | |||
| 0 | 0.00379722 | 0.00375311 | 0.00004410 |
| 1 | 0.00328998 | 0.00328462 | 0.00000536 |
| 2 | 0.00291427 | 0.00287461 | 0.00003966 |
| 3 | 0.00250378 | 0.00251579 | 0.00001200 |
| 4 | 0.00225176 | 0.00220175 | 0.00005001 |
| 5 | 0.00190450 | 0.00192691 | 0.00002241 |
| 6 | 0.00172045 | 0.00168638 | 0.00003407 |
| 7 | 0.00145947 | 0.00147588 | 0.00001640 |
| 8 | 0.00129005 | 0.00129165 | 0.00000159 |
| 9 | 0.00109247 | 0.00113042 | 0.00003795 |
| 10 | 0.00092289 | 0.00098931 | 0.00006642 |
| 11 | 0.00074314 | 0.00086582 | 0.00012268 |
| 12 | 0.00056520 | 0.00075774 | 0.00019254 |
| 13 | 0.00038370 | 0.00066315 | 0.00027946 |
| 14 | 0.00020306 | 0.00058037 | 0.00037731 |
| 15 | 0.00002275 | 0.00050793 | 0.00048518 |
Текст программы смотри в приложении 2
Похожие работы
... на первой и последующих итерациях равна: ; (3.22) . (3.23) Критерием завершения итерационного процесса является условие: ,(3.24) где - заданная точность расчета [4]. 4. Методы оценки термонапряженного состояния 4.1 Физические основы возникновения термических напряжений При изменении температуры происходит объемное расширение или сжатие твердого тела. Неравномерный нагрев ...
... диаметрах критического сечения представлены на рисунке 2.24 Рисунок 2.24 - Зависимость оптимальной высоты поднятия фурмы от давления при различных диаметрах критического сечения сопла Лаваля 3. Численное исследование движения жидкости Приведены уравнения Навье - Стокса установившегося осесимметричного движения несжимаемой вязкой жидкости в переменных функция тока - вихрь. Проведено ...
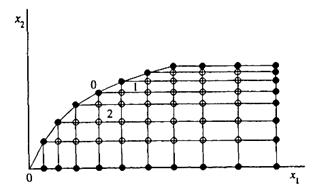
... системы на ЭВМ, а так же требование его экономичности обуславливают применение регулярных сеток, расположение узлов в которых подчиняется определённым закономерностям. В практике численного моделирования микроэлектронных структур примеяются как непрерывные прямоугольные (неравномерные), так и треугольные сетки (рис.2.). Треугольная сетка позволяет с меньшим количеством дополнительных узлов сгущать ...
... . Реакции узлов более высокого уровня менее зависят от позиции и более устойчивы к искажениям. Структура Неокогнитрон имеет иерархическую структуру, ориентированную на моделирование зрительной системы человека. Он состоит из последовательности обрабатывающих слоев, организованных в иерархическую структуру (рис. 10.8). Входной образ подается на первый слой и передается через плоскости, ...
0 комментариев