Навигация
Неравномерная сетка
1.7 Неравномерная сетка
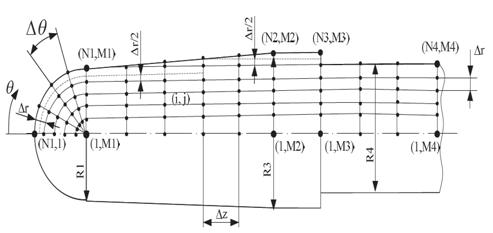
1.7.1 Построение сеточной области
Пусть исходная область ![]() ={
={![]() }. Ее аппроксимируем сеточной областью:
}. Ее аппроксимируем сеточной областью:
![]()
![]() ,
, ![]()
![]()
![]() - средний шаг}- сетка по х;
- средний шаг}- сетка по х;
![]()
![]() ,
, ![]()
![]()
![]() - средний шаг}- сетка по t;
- средний шаг}- сетка по t;
Тогда искомая сетка есть ![]() - неравномерная сетка.
- неравномерная сетка.
На этой сетке аппроксимируем дифференциальные операторы:
![]() - правая разностная производная по х; (1)
- правая разностная производная по х; (1)
![]() -сеточная функция;
-сеточная функция;
![]() - левая разностная производная по х; (2)
- левая разностная производная по х; (2)
![]() - центральная разностная производная по х; (3)
- центральная разностная производная по х; (3)
![]()
![]() - аппроксимация с весом
- аппроксимация с весом ![]() ; (4)
; (4)
![]() Аппроксимация первой производной по t имеет вид:
Аппроксимация первой производной по t имеет вид:
![]() - правая разностная производная по t; (5)
- правая разностная производная по t; (5)
![]() - левая разностная производная по t; (6)
- левая разностная производная по t; (6)
![]() - центральная разностная производная по t; (7)
- центральная разностная производная по t; (7)
Аппроксимация второй производной по х и по t имеет вид:
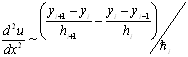 ; (8)
; (8)
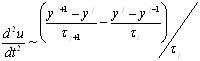 ; (9)
; (9)
Покажем погрешность аппроксимации первой производной по х.
Для этого введем функцию погрешности решения ![]() Найдем
Найдем ![]() и подставим в (1).
и подставим в (1).
Имеем ![]() =
=![]() ,
, ![]()
Функцию ![]() разложим по формуле Тейлора
разложим по формуле Тейлора
![]() ,
,
и подставим в ![]() Имеем
Имеем
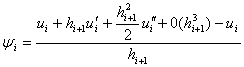
![]() ,
,
отсюда получаем аппроксимацию первого порядка ![]() .
.
1.7.2 Формирование сетки
I вариант
![]() ,
,![]() (1)
(1)
![]() , q>1-возраст.геометр.прогрессия
, q>1-возраст.геометр.прогрессия
![]() , q<1-убыв.геометр.прогрессия
, q<1-убыв.геометр.прогрессия
1) ![]() , (2)
, (2)
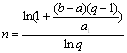 , q>1. (3)
, q>1. (3)
2) ![]() , (4)
, (4)
![]() , q<1. (5)
, q<1. (5)
![]() и
и ![]() - задаем сами.
- задаем сами.
Пример Пусть ![]()
![]()
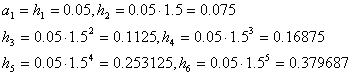
q>1 и по формуле (3) n![]()
![]()
Пример Пусть ![]()
вычисляем по формуле (5)
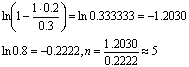
Действительно

II вариант
Можно использовать другой подход:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
a) ![]() , q<1 - убывающая геом. прогрессия n и q-задаем сами.
, q<1 - убывающая геом. прогрессия n и q-задаем сами.
в) ![]() , q>1 – возрастающая геом. прогрессия.
, q>1 – возрастающая геом. прогрессия.
Таким образом, можно рассматривать следующие модули сеток:
1) Равномерная сетка ![]() .
.
2) Квазиравномерная сетка (![]() …).
…).
3) Неравномерная по возрастающей геометрической прогрессии ![]() .
.
4) Неравномерная по убывающей геометрической прогрессии ![]() .
.
5) Среднеарифметический метод 3) и 4) ![]() .
.
Глава II. Одномерное уравнение переноса с переменными коэффициентами
Похожие работы
... на первой и последующих итерациях равна: ; (3.22) . (3.23) Критерием завершения итерационного процесса является условие: ,(3.24) где - заданная точность расчета [4]. 4. Методы оценки термонапряженного состояния 4.1 Физические основы возникновения термических напряжений При изменении температуры происходит объемное расширение или сжатие твердого тела. Неравномерный нагрев ...
... диаметрах критического сечения представлены на рисунке 2.24 Рисунок 2.24 - Зависимость оптимальной высоты поднятия фурмы от давления при различных диаметрах критического сечения сопла Лаваля 3. Численное исследование движения жидкости Приведены уравнения Навье - Стокса установившегося осесимметричного движения несжимаемой вязкой жидкости в переменных функция тока - вихрь. Проведено ...
... системы на ЭВМ, а так же требование его экономичности обуславливают применение регулярных сеток, расположение узлов в которых подчиняется определённым закономерностям. В практике численного моделирования микроэлектронных структур примеяются как непрерывные прямоугольные (неравномерные), так и треугольные сетки (рис.2.). Треугольная сетка позволяет с меньшим количеством дополнительных узлов сгущать ...
... . Реакции узлов более высокого уровня менее зависят от позиции и более устойчивы к искажениям. Структура Неокогнитрон имеет иерархическую структуру, ориентированную на моделирование зрительной системы человека. Он состоит из последовательности обрабатывающих слоев, организованных в иерархическую структуру (рис. 10.8). Входной образ подается на первый слой и передается через плоскости, ...
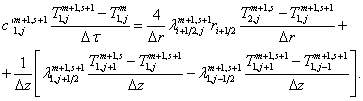
0 комментариев