Определение траектории выходного звена механизма сопла

3.4 Определение траектории выходного звена механизма сопла

Модернизированный механизм сопла автосъемника бобин представляет собой плоский кулачковый коромысловый механизм.

Очевидно, что для профилирования кулачка данного механизма необходимо определить: траекторию выходного звена механизма сопла и конструктивные параметры коромысла.

Выходное звено механизма сопла при своем движении должно пройти несколько характерных точек. Этими точками являются: 1 – исходная точка, находясь в которой сопло имеет возможность передвижения вдоль фронта машины; 2 – точка входа сопла в зону обрезки и захвата нити; 3 – точка, определяющая продолжительность выстоя сопла в зоне обрезки и захвата нити; 4 – крайняя верхняя точка сопряжения поверхности сопла с поверхностью рычага захвата и смены патронов при совместном движении механизма сопла с механизмом захвата и смены патронов; 5 – точка прохождения сопла около поверхности патрона, установленного в рычаги бобинодержателя, опускающего патрон на мотальный вал; 6 – точка, находящаяся в зоне захвата нити между мотальным валом и установленным парном; 7 – точка, совпадающая с характерной точкой 1.

Определим траекторию выходного звена механизма сопла. Между характерными точками 1 и 2 траектория определяется дугой окружности; между характерными точками 2 и 3 траектория определяется прямой линией; между характерными точками 3 и 4 траектория определяется дугой окружности; между характерными точками 4 и 5, 5 и 6, 6 и 7 траектории определяются кубическими сплайнами. Траектория выходного звена механизма сопла представлена на рис. 56 и определяется следующими уравнениями:

участок 1–2: ,

где  – координаты точки подвеса коромысла;  – максимальное расстояние от точки подвеса коромысла до крайней точки звена, равное:

,

где  – общая длина коромысла;  – длина сопла;  – угол наклона сопла;

участок 2–3: ,

где k и b – параметры прямой, определяемой конструктивным расположением направляющего бруса;

участок 3–4: ,

где ,  – координаты крайнего правого положения шарнира, установленного на конце коромысла;

участок 4–5: ,

где , , ,  – коэффициенты кубического сплайна;

участок 5–6: ,

где , , ,  – коэффициенты кубического сплайна;

участок 6–7: ,

где , , ,  – коэффициенты кубического сплайна.

Для определения коэффициентов , , ,  на всех n элементарных отрезках необходимо получить  уравнений. Часть из них вытекает из условий прохождения графика функции  через заданные точки, т.е. . Эти условия можно записать в виде:

,

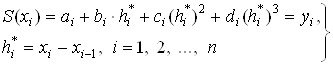
Вычислим производные кубического сплайна:

Приравнивая в каждом внутреннем узле  значения этих производных, вычисленные в левом и правом от узла интервалах, получаем  уравнений:

,

.

Недостающие два соотношения получаются из условий закрепления концов сплайна.

В частности, при свободном закреплении концов можно приравнять нулю кривизну линии в этих точках. Такая функция, называемая свободным кубическим сплайном, обладает свойством минимальной кривизны, т.е. она самая гладкая среди всех интерполяционных функций данного класса. Из условий нулевой кривизны на концах следуют равенства нулю вторых производных в этих точках:

, .

Уравнения … составляют систему линейных алгебраических уравнений для определения  коэффициентов , , , . Эту систему решаем методом Гаусса, изложенным в курсе программирования и имеющимся в банке стандартных программ, введенных в память ЭВМ.