Навигация
Вычисляем коэффициенты k и b, используя подпрограмму KOR
2. Вычисляем коэффициенты k и b, используя подпрограмму KOR.
3. Приравниваем ![]() ,
, ![]() .
.
4. Примем в качестве начального приближения координаты точки ![]() . Для вызова подпрограммы KOR примем:
. Для вызова подпрограммы KOR примем: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
5. Вычисляем коэффициенты k и b.
6. Приравняем ![]() ,
, ![]() .
.
7. Решаем систему уравнений двух прямых:
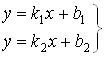 ,
,
откуда следует, что
![]() ,
, ![]()
и ![]() ,
, ![]()
где ![]() ,
, ![]() – координаты шарнира коромысла, на котором установлено сопло.
– координаты шарнира коромысла, на котором установлено сопло.
Тогда ![]() ,
,
![]() ,
,
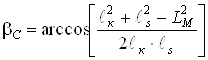 .
.
8. Выводим на печать ![]() .
.
9. Идем вдоль стороны AD, при этом значение x будет в пределах от ![]() до
до ![]() , шаг
, шаг ![]() , вычисляем значение
, вычисляем значение ![]() .
.
10. Вызываем подпрограмму KOR.
11. Доходим до вершины D, идем вдоль стороны BD, при этом значение x будет в пределах от ![]() до
до ![]() , вычисляем значение
, вычисляем значение ![]() .
.
12. Доходим до вершины B, идем вдоль стороны AB, при этом значение ![]() будет в пределах от
будет в пределах от ![]() до
до ![]() , вычисляем значение
, вычисляем значение ![]() .
.
Значения выходных параметров в точках A, B и D будут вычислены дважды.
Подпрограмма KOR решает задачу нахождения координат общей точки касательной и окружности, к которой она проведена.
Алгоритм решения данной задачи также представим словесно-формульным описанием:
1. Задается точка ![]() с координатами
с координатами ![]() и
и ![]() , из которой проводится касательная к окружности с радиусом
, из которой проводится касательная к окружности с радиусом ![]() , центр которой задан координатами
, центр которой задан координатами ![]() и
и ![]() .
.
2. Решаем систему уравнений двух окружностей:
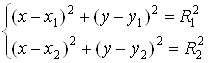 ,
,
где ![]() и
и ![]() ;
; ![]() – расстояние между точками
– расстояние между точками ![]() и
и ![]() ;
; ![]() – расстояние от точки
– расстояние от точки ![]() до точки касания прямой с окружностью;
до точки касания прямой с окружностью; ![]() и
и ![]() – координаты точки касания.
– координаты точки касания.
После преобразований получим:
![]() .
.
Пусть ![]() ,
,
![]() ,
, ![]() .
.
Тогда ![]() или
или ![]() ,
,
где ![]() ,
, ![]() .
.
После преобразований получим:
![]() ,
,
где 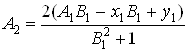 ,
,
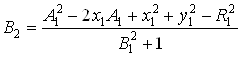 ,
,
 .
.
0 комментариев