Навигация
Оптимизация конструктивных параметров коромысла нового механизма сопла
3.5 Оптимизация конструктивных параметров коромысла нового механизма сопла
Вторая задача, а именно определение конструктивных параметров коромысла механизма сопла, заключается в выявлении общей длины ![]() коромысла, длины
коромысла, длины ![]() сопла и угла наклона
сопла и угла наклона ![]() сопла.
сопла.
Очевидно, что поставленная задача требует оптимизации вышеназванных параметров коромысла механизма сопла, которую необходимо провести с целью выбора наилучшего варианта. Выбор оптимального решения или сравнение двух альтернативных решений проведем с помощью некоторой целевой функции, определяемой проектными параметрами. В процессе решения задачи оптимизации должны быть найдены значения проектных параметров, при которых целевая функция имеет экстремум.
Целевую функцию оптимизации проектных параметров коромысла механизма сопла можно записать в виде:
![]() ,
,
где ![]() – наименьший угол между коромыслом и соплом в исходном положении механизма.
– наименьший угол между коромыслом и соплом в исходном положении механизма.
Поскольку число проектных параметров целевой функции равно трем, то графиком целевой функции будет являться поверхность в пространстве, но для наглядности выбора принимаемого решения будем строить график каждой переменной отдельно в виде кривой на плоскости. Задача оптимизации конструктивных параметров механизма сопла относится к задачам с ограничениями, т.е. имеется зависимость между проектными параметрами, которые должны учитываться при нахождении решения. Этой зависимостью является соотношение.
Таблица 7. Координаты точек траектории выходного звена механизма сопла на участке 4–5
|
| ||
|
| ||
| Порядковый номер точки траектории | Абсцисса x точки траектории, мм | Ордината y точки траектории, мм |
| 1 2 3 4 5 6 7 | 221 218 215 212 209 206 203 | -74,99999 -101,88160 -128,00979 -153,38510 -178,00825 -201,87970 -225,00001 |
Таблица 8. Координаты точек траектории выходного звена механизма сопла на участке 5–6
|
| ||
|
| ||
| Порядковый номер точки траектории | Абсцисса x точки траектории, мм | Ордината y точки траектории, мм |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | 203 200 197 194 191 188 185 182 179 176 173 170 167 164 161 158 | -225 -231,72336 -238,24891 -244,57649 -250,70592 -256,63701 -262,36959 -267,90347 -273,23849 -278,37446 -283,31121 -288,04854 -292,58630 -296,92430 -301,06236 -305,00030 |
При этом заданы длина звена ![]() , определяющая положение установки ролика на коромысле, и радиус
, определяющая положение установки ролика на коромысле, и радиус ![]() кулачка, определяющий минимальный угол отклонения коромысла. Кроме того, задана точка, определяющая центр положения патрона
кулачка, определяющий минимальный угол отклонения коромысла. Кроме того, задана точка, определяющая центр положения патрона ![]() при верхнем крайнем правом положении рычага захвата и смены патронов, а также задан радиус
при верхнем крайнем правом положении рычага захвата и смены патронов, а также задан радиус ![]() поверхности этого рычага, сопрягаемой с поверхностью сопла. Целевую функцию находим симплекс-методом, заключающимся в следующем: примем в качестве начального приближения координаты некоторой вершины многогранника допустимых решений и найдем все ребра, выходящие из этой вершины, двигаясь вдоль того ребра, по которому линейная целевая функция убывает, приходим в новую вершину. Находим все выходящие из нее ребра, двигаемся по одному из них и т.д. В конце концов придем в такую вершину, движение из которой вдоль любого ребра приводит к возрастанию целевой функции. Следовательно, минимум достигнут, и координаты этой последней вершины принимаются в качестве оптимальных значений рассматриваемых проектных параметров. Поскольку в нашем случае параметры
поверхности этого рычага, сопрягаемой с поверхностью сопла. Целевую функцию находим симплекс-методом, заключающимся в следующем: примем в качестве начального приближения координаты некоторой вершины многогранника допустимых решений и найдем все ребра, выходящие из этой вершины, двигаясь вдоль того ребра, по которому линейная целевая функция убывает, приходим в новую вершину. Находим все выходящие из нее ребра, двигаемся по одному из них и т.д. В конце концов придем в такую вершину, движение из которой вдоль любого ребра приводит к возрастанию целевой функции. Следовательно, минимум достигнут, и координаты этой последней вершины принимаются в качестве оптимальных значений рассматриваемых проектных параметров. Поскольку в нашем случае параметры ![]() зависят от угла наклона касательной к окружности, поэтому за многогранник допустимых решений примем треугольник ABD, вершины которого заданы координатами:
зависят от угла наклона касательной к окружности, поэтому за многогранник допустимых решений примем треугольник ABD, вершины которого заданы координатами: ![]() ,
, ![]() ,
, ![]() . Определим уравнение прямых, проходящих через две точки, а именно: через А и D, B и D и через А и B.
. Определим уравнение прямых, проходящих через две точки, а именно: через А и D, B и D и через А и B.
Таблица 9. Координаты точек траектории выходного звена механизма сопла на участке 6–7
|
| ||
|
| ||
| Порядковый номер точки траектории | Абсцисса x точки траектории, мм | Ордината y точки траектории, мм |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 158 155 152 149 146 143 140 137 134 131 128 125 122 119 116 | -305 -307,20940 -309,33684 -311,38208 -313,34496 -315,22521 -317,02267 -318,73710 -320,36830 -321,91605 -323,38016 -324,76040 -326,05656 -327,26845 -328,39583 |
Имеем следующие параметры прямых, проходящих через эти точки:
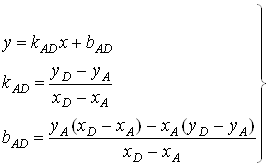 ,
,
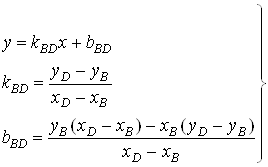 ,
,
 .
.
Алгоритм решения задачи представим словесно-формульным описанием:
1. Определим уравнение прямой, являющейся касательной к кулачку с радиусом ![]() . При этом известна точка вращения кулачка, радиус
. При этом известна точка вращения кулачка, радиус ![]() кулачка, точка подвеса коромысла и длина
кулачка, точка подвеса коромысла и длина ![]() , определяющая точку крепления ролика на коромысле. Для вызова подпрограммы KOR следует принять:
, определяющая точку крепления ролика на коромысле. Для вызова подпрограммы KOR следует принять: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
0 комментариев