Проверочный расчет передачи

2.3 Проверочный расчет передачи

Определяем контактные напряжения [5, с.6]

 (4)

где

KH = KHa · KHb · KHn

Для передач с круговыми зубьями [6]

KHa = 1 + 2,1 x 10-6 x  x V + 0,02 x (nст – 6)1,35 = 1,07365

KHn - определяем по табл. 10, KHn = 1,035

KH = 1,1112

Вычисляем sн по формуле (4)

604,911 МПа < 660 МПа

Определяем:

= 8,347 %

Допускаются превышения напряжений sн над sнр не более чем на 5%.

Если это условие не выполняется, то выбирают ближайшее стандартное значение dе2 и повторяют расчет. Если DН > 20%, то выбирают ближайшее меньшее стандартное значение dе2.

Проверяют зубья шестерни и колеса на выносливость по напряжениям изгиба, использую формулы [5, с.7]

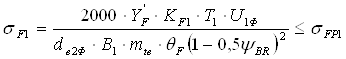 (5)

sF2 = sF1 · /  £ sFP2 ,

где для колес с круговыми зубьями q F принимают по табл.5.

q F = 0,85 + 0,043 · 3,55 = 1

Коэффициент нагрузки определяется по формуле: [5, с. 7]

KF = KFa · KFb · KFn = 1,04

где KFa для колес с круговыми зубьями определяется по формуле:

KFa = [4 + (ea - 1) · (nст - 5)] / (4 x ea) = 0,942

где ea - коэффициент перекрытия для передач с круговыми зубьями ea = 1,3;

KFb = 1 + 1,5 x (KНb -1) = 1

KFn находим по выражению:

KFn = 1 + dF · (KHn - 1) / dH = 1,105

Где dН и dF - коэффициенты, учитывающие влияние вида зубчатой передачи и модификацию профиля головок зубьев [4, с. 37], (табл. 11), dН = 0,002; dF = 0,006

Коэффициент формы зуба

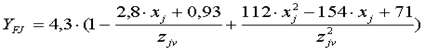
где Zjv - эквивалентное число зубьев, определяется по формуле

Zjv = Zj / (cos dj x cos3 bm)

Z1v = Z1 / (cos d1 · cos3 bm) = 34,3416

Z2v = Z2 / (cos d2 · cos3 bm) = 344,37

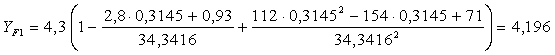
Определяем sF1 по формуле (5)

sF2 = 173,24 · 4,549 / 4,196 = 186 < 192 МПа

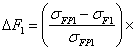100% = 27,5 %

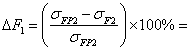3,13 %

Допускается превышение напряжений sFj над sFPj не более чем на 5%.

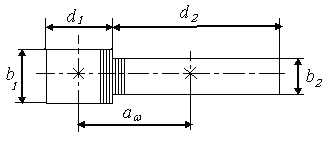
2.4 Определение геометрических размеров зубчатых колес

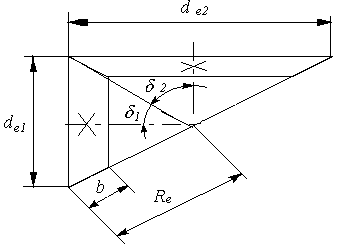
Диаметр внешней делительной окружности шестерни и колеса с точностью до 0,001 мм.

d e1 = z 1 · mte = 17 · 5,063825 = 86,085 мм

d e2 = z 2 · mte = 60 · 5,063825 = 303,8295 мм

Внешние диаметры вершин зубьев:

dаe1 = d e1 + 2·(1 + х1) mte · cos d1 · cosbm = 104,3635 мм

d аe2 = d e2 +2·(1 + х2) mte · cosd2 · cosbm = 309,0084 мм

Внешние высоты головок и ножек зубьев:

hаe1 = (1 + х1) mte · cosbm = 9,5 мм

hаe2 = (1 - х2) mte · cosbm = 6,438 мм

hfe1 = (1,2 + х1) mte · cosbm = 6,55 мм

hfe2 = (1,2 - х2) mte · cos bm = 4,15 мм

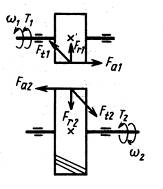
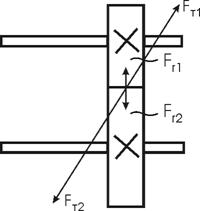
2.5 Определение сил в конической зубчатой передаче

Окружная сила на среднем диаметре:

Ft1 = 2T1 · 103 / dm1 = 6581,4 Н

Для передачи с круговыми зубьями осевая сила на шестерне при совпадении направления ее вращения с направлением наклона зуба шестерни определяется:

Fа1 = Ft1 · (0,44 · sind1 + 0,7 · cosd1) = 5222 Н

При противоположном направлении ее вращения:

Fа1¢ = Ft1 · (0,44 · sin d1 – 0,7 · cos d1) = - 3643 Н

Радиальная сила на шестерне для первого случая:

Fr1 = Ft1 · (0,44 · cosd1 – 0,7 · sind1) = 1530 Н

Для второго случая:

Fr1¢ = Ft1 · (0,44 ·cosd1 + 0,7 · sind1) = 4042 Н

Осевая и радиальная силы на колесе соответственно равны:

Fа2 = Fr1 = 1530 Н Fr2 = Fа1 = 5222 Н

Fа2¢ = Fr1¢ = 4042 НFr2¢ = Fа1¢ = -3643 Н

3. Расчет цилиндрической зубчатой передачи тихоходной ступени

3.1 Выбор материалов и допускаемые напряжения

Диаметры заготовок для шестерни и колеса косозубой передачи

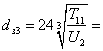 143,15 мм

dз4 = dз3 · U2 = 143,15 · 4,5 = 644,2 мм

Размеры характерных сечений заготовок:

Sc3 = 0,5 · dз3 = 0,5 · 143,15 = 71,58 мм

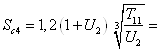
Для колес тихоходной передачи выбираем такие же материалы, как и для колес быстроходной передачи (см. п. 2.1).

В этом случае при расчете допускаемых контактных напряжений по формуле (1):

Для шестерни:

 1059 МПа

SH3 = SH1 = 1,2;

NНО3 = NНО1 = 8,69 · 107

Для колеса:

641 МПа

SH4 = SH2 = 1,1

NНО4 = NНО2 = 2,35 · 107

Определяем эквивалентное число циклов напряжений

NНЕj = Nåj · KНЕ ,

где KНЕ = 0,18 (см. п. 2.1).

Nåj = 60 · tå · n j ;

Nå3 = 60 · tå · n 11 = 60 · 10 000 · 207 = 124,2 · 106

Nå4 = 60 · tå · n 111 = 60 · 10 000 · 46 = 27,6 · 106

NНЕ3 = Nå3 · KНЕ = 124,2 · 106 · 0,18 = 25,356 · 106

NНЕ4 = Nå4 · KНЕ = 29,3 · 106 · 0,18 = 5,274 · 106

Находим коэффициент долговечности:

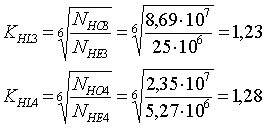
Определяем допускаемые контактные напряжения:

 1059 / 1,2 · 1,2 = 1085 МПа

 641 / 1,1 · 1,28 = 745,89 МПа

При расчете косозубых и шевронных передач sHP выбирается как наименьшее из двух, получаемых по формулам.

sHP = 0,45 · (sHP3 + sHP4 ) = 823,9 МПа

sHP = 1,23 · sHPj min = 1,23 · sHP4 = 917,44 МПа

Выбираем наименьшее из полученных значений sHP = 823,9 МПа

При расчете допускаемых напряжений изгиба по формуле (2):

для шестерни:

 600 МПа

SF3 = SF1 = 1,9

KFC3 = KFC1 = 0,75

KFE3 = KFE1 = 0,04

для колеса:

485 МПа

SF4 = SF2 = 1,65

KFC4 = KFC2 = 0,65

KFE4 = KFE2 = 0,06

Для определения коэффициента долговечности находим эквивалентное число циклов напряжений N FЕj :

NFЕ3 = Nå3 · KFЕ3 = 139,2 · 106 · 0,04 = 5,56 · 106

NFЕ4 = Nå4 · KFЕ4 = 29,3 · 106 · 0,06 = 1,758 · 106

При N FЕj ³ N FО = 4 · 106 принимаем КFL3 = 1, а

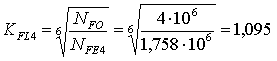
Определяем допускаемые напряжения изгиба по формуле (2)

 600 / 1,9 · 1 · 0,75 = 237 МПа

 485 / 1,65 · 1,095 · 0,65 = 209 МПа

3.2 Определение геометрических размеров передачи

Ориентировочно рассчитываем величину межосевого расстояния [6, с.3]

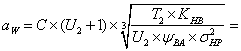240,76 мм

где с=430 для косозубых и шевронных передач;

yBA – коэффициент ширины венца по межосевому расстоянию, который выбирают из единого ряда, рекомендованного ГОСТ 2185-66 [7табл. 12] с учетом расположения опор относительно зубчатого венца [7 табл. 13], yBA =0,315

KHb - коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; для определения KHb можно воспользоваться зависимостью [6, с.3].

KHb = 1 + KHСb · (ybd )4/3 = 1 + 0,072 · 0,90564/3 = 1,063

Где

KHС =0,47 · gt / KСX

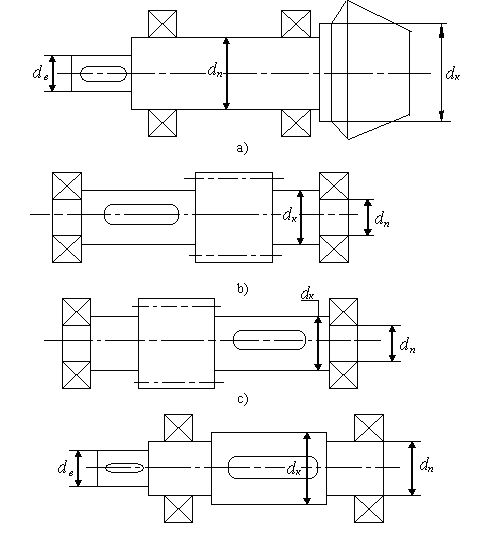
здесь KСX - коэффициент, зависящий от номера схемы (табл. 13);

KСX=6,5; КНС = 0,47 · 1 / 6,5 = 0,072

gt = 1 при твердости активной поверхности зубьев НВj min £ 350;

ybd - коэффициент ширины венца по диаметру;

ybd = 0,5 · ybа · (U2 + 1) = 0,5 · 0,315 · (4,5 + 1) = 0,866

Округляем aw до ближайшего стандартного значения по ГОСТ 2185-66 [7табл. 14], aw = 250 мм

Находим ориентировочную ширину колеса:

bw‘ = yba · aw = 0,315 · 250 = 78,75 мм

и ширину шестерни:

bw3‘ =1,1 · bw4‘ = 1,1 · 78,75 = 86,63 мм

Округляем их до ближайшего значения из ряда Rа 20 [7, табл.9], bw4 = 80 мм и bw3 = 85 мм

Определяем диаметры начальных окружностей шестерни и колеса:

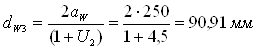
dw4 = dw3 · U2= 90,91 · 4,5 = 409,1 мм

Находим окружную скорость в зацеплении

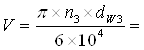3,14 · 232 · 69,5652 / 6 · 104 = 0,985 м/с

Степень точности цилиндрической передачи можно определить по формулам:

nст = 10,1 – 0,12 · V b > 0.

Если в результате расчета будет получено nст > 9, то нужно принять nст = 9.

Ориентировочно находим степень точности передачи

nст¢= 10,1 – 0,12 · V = 10,1 –0,12 · 0,985 = 9,982

принимаем nст = 9

Ориентировочно находим модуль передачи по формуле [6, с.6]

4400·955·(4,5+1)/250·85·237=4,588мм

km= 4400 для косозубых передач

Округляем mn‘ до ближайшего большего стандартного значения [7табл. 15], учитывая, что применение модуля меньше 2 мм для силовых передач нежелательно,

mn = 5

При выборе узла наклона зуба в косозубых передачах принимают во внимание ограничение по коэффициенту осевого перекрытия eb ³ 1,1, из которого следует

b‘ ³ bmin = arcsin · (1,1p · mn / bw4 )= arcsin · (1,1 · 3,14 · 5 / 80 )= =12,473º (7)

Угол наклона зуба в косозубых передачах выбирают в диапазоне 8°…16°. Если bmin попадает в указанный диапазон, следует принять предварительное значение угла наклона зуба b¢ = bmin , при bmin < 8° принимаем b‘= 16°, наконец, при bmin > 16° вместо первоначально выбранного значения yва принимают ближайшее большее стандартное значение yва и вновь проверяют условие (7).

Ориентировочно принимаем b‘= 15º

Рассчитываем ориентировочно суммарное число зубьев шестерни и колеса:

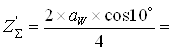 2 · 250 · cos(15) / 5 = 96,6 (8)

Округляем Zå' до ближайшего целого числа Zå = 97

Находим ориентировочно число зубьев шестерни:

Z3' = Zå /(U2 + 1) = 97/(4,5+1) = 17,63

Округляем Zå' до ближайшего целого числа Zå = 18

Определяем число зубьев колеса:

Z4 = Zå - Z3 = 97-18=79

Уточняем передаточное число:

U2Ф = Z4 / Z3 = 79/18 = 4,3888

Расхождение с принятым ранее номинальным передаточным числом не должно превышать ± 2,5% при U £ 4, и ± 4% при U > 4,5. Если это условие не выполняется, то при U > UФ увеличиваем Z4 и Z3 на единицу, оставляя неизменным Z3, а при U < UФ уменьшаем Z4 и Z3 на единицу.

Для нашего примера:

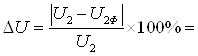2,469% < 2,5%

Уточняем значение угла наклона зуба

b = arccos [(zå · mn) /(2 · aw )] = arccos (97 · 5 / 2 · 250) = 14,07° = 14°4'11,52''