Навигация
Многофакторный корреляционно – регрессионный анализ безработицы
3.3. Многофакторный корреляционно – регрессионный анализ безработицы
Таблица 10. Исходные данные.
| год | Уровень безраб-цы | Индекс ВРП | Доход на душу насел-я | Доля пенсионеров |
| 1992 | 5,8 | 77,3 | 51,7 | 18,7 |
| 1993 | 5,9 | 93,3 | 137,4 | 19,6 |
| 1994 | 9,8 | 85,5 | 11,2 | 20,2 |
| 1995 | 12,7 | 86,2 | 83,7 | 20,9 |
| 1996 | 14,9 | 93,5 | 89,6 | 21,5 |
| 1997 | 21,3 | 102,2 | 130,5 | 22,1 |
| 1998 | 22,2 | 94,2 | 72,2 | 22,5 |
| 1999 | 17,3 | 108 | 99,9 | 22,8 |
| 2000 | 19,1 | 104,9 | 111,2 | 22,9 |
| 2001 | 18,4 | 106,4 | 110,2 | 23,2 |
| 2002 | 15,4 | 106,4 | 121,5 | 23,3 |
| 2003 | 16,8 | 106,7 | 104,5 | 23,3 |
| 2004 | 15,3 | 103,7 | 104,4 | 23,5 |
| 2005 | 12 | 104,8 | 111,3 | 23,8 |
| итого | 206,9 | 1373,1 | 1339,3 | 308,3 |
| средн | 14,779 | 98,079 | 95,664 | 22,0214 |
Для корреляционно-регрессионного анализа необходимо из нескольких факторов произвести предварительный отбор факторов для регрессионной модели. Сделаем это по итогам расчета коэффициента корреляции. А именно возьмем те факторы, связь которых с результативным признаком будет выражена в большей степени. Начнем наш анализ с рассмотрения следующих факторов:
- Индекс ВРП - x1 (%)
- Доход на душу населения – x2 (%)
- Доля пенсионеров - x3 (%)
Рассчитаем коэффициент корреляции для линейной связи и для имеющихся факторов - x1, x2 и x3. Коэффициент корреляции определяется по следующей формуле:
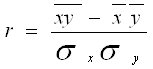
где: ![]() и
и ![]() – дисперсии факторного и результативного признака соответственно; xy – среднее значение суммы произведений значений факторного и результативного признака; x и y – средние значения факторного и результативного признака соответственно.
– дисперсии факторного и результативного признака соответственно; xy – среднее значение суммы произведений значений факторного и результативного признака; x и y – средние значения факторного и результативного признака соответственно.
Для фактора x1 получаем коэффициент корреляции r1: r1= 0,627
Для фактора x2 получаем коэффициент корреляции r2: r2 =0,295
Для фактора x3 получаем коэффициент корреляции r3: r3=0,717
По полученным данным можно сделать вывод о том, что:
1)Связь между x1 и y прямая (так как коэффициент корреляции положительный) и умеренно сильная. Поэтому, будем использовать фактор в дальнейших расчётах.
2)Связь между x2 и y прямая (так как коэффициент корреляции положительный) и умеренная, так как она находится между 0,21 и 0,30. Таким образом, возникает необходимость исключить данный фактор из дальнейших исследований.
3)Связь между x3 и y прямая (так как коэффициент корреляции положительный) и сильная. Также будем использовать данный фактор в дальнейших расчетах.
Таким образом, два наиболее влиятельных фактора - индекс ВРП и доля пенсионеров. Для имеющихся факторов x1 и x3 составим уравнение множественной регрессии. Для анализа воспользуемся линейной формой связи, т.е. составим линейное уравнение, т.к. линейное уравнение легче подвергать анализу, интерпретации.
Проверим факторы на мультиколлинеарность, для чего рассчитаем коэффициент корреляции rx1x3:
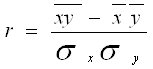
где: ![]() и
и ![]() – дисперсии факторного и результативного признака соответственно; x,y – среднее значение суммы произведений значений факторного и результативного признака; x и y – средние значения факторного и результативного признака соответственно.
– дисперсии факторного и результативного признака соответственно; x,y – среднее значение суммы произведений значений факторного и результативного признака; x и y – средние значения факторного и результативного признака соответственно.
Подставив имеющиеся данные (из таблицы 10) в формулу, имеем следующее значение: rx1x3=0,8998.Полученный коэффициент говорит об очень высокой связи, поэтому дальнейший анализ по обоим факторам вестись не может. Однако в учебных целях продолжим анализ.
Проводим оценку существенности связи с помощью коэффициента множественной корреляции:
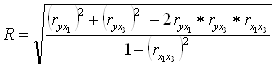
где: ryx1 – коэффициент корреляции между y и x1; ryx3 – коэффициент корреляции между y и x3; rx1x3 – коэффициент корреляции между x1 и x3.
Подставив имеющиеся данные в формулу и получим: R=0,717
Так как R < 0,8, то связь признаем не существенной, но, тем не менее, в учебных целях, проводим дальнейшее исследование.
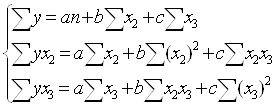 |
Уравнение прямой имеет следующий вид: ŷ = a + bx1 + cx3
Для определения параметров уравнения необходимо решить систему:
Решив систему, получим уравнение: Ŷ=14,72+0,00023 x1+0,00086x3
Для данного уравнения найдем ошибку аппроксимации:
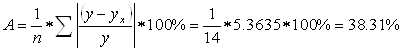
А> 5%, то данную модель нельзя использовать на практике.
Проведем оценку параметров на типичность. Рассчитаем значения величин:
S2=28,039
ma=1,415; mb=0,023; mс=0,8404;
ta=10,403; tb=0,01; tc=0,001.
Сравним полученные выше значения t для α = 0,05 и числа степеней свободы (n-2) с теоретическим значением t-критерия Стьюдента, который tтеор = 2,1788. Расчетные значения tbи tс < tтеор, значит данные параметры не значимы и данное уравнение не используется для прогнозирования.
Далее оценим существенность совокупного коэффициента множественной корреляции на основе F-критерия Фишера по формуле:
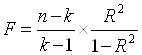
где: n – число уровней ряда; к – число параметров; R – коэффициент множественной корреляции.
После расчета получаем: F=5,819
Сравним Fрасч с Fтеор для числа степеней свободы U1 = 9 и U2 = 2, видим, что 0,045 < 19,40, то есть Fрасч < Fтеор - связь признаётся не существенной, то есть корреляция между факторами x1, x3 и у не существенна.
Похожие работы
... степень сбалансированности системы подготовки кадров с потребностью экономики в квалифицированных работниках. 6.2. Статистика занятости и безработицы Занятость - одна из важнейших социально-экономических проблем рыночной экономики. Ее статистическое отражение неоднократно обсуждалось на международных конференциях статистиков труда (1949, 1957, 1982, 1993 гг.), проводимых Международным бюро ...
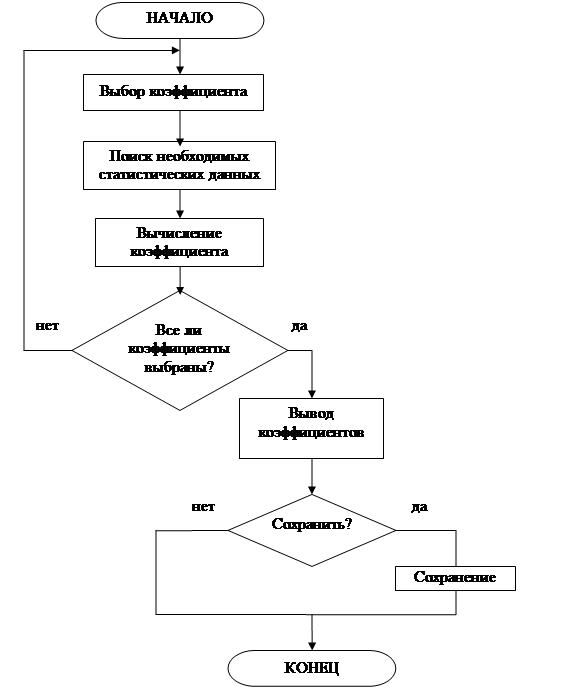
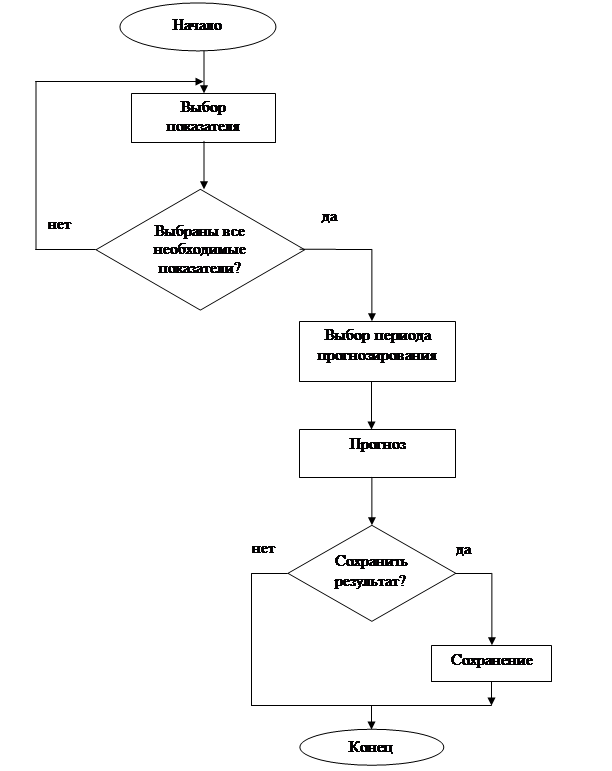
... с распространением явления неполная занятость: , (1.11) где ТНЗ– численность занятых неполное рабочее время [1]. 2 ПРОЕКТНАЯ ЧАСТЬ В курсовом проекте для проведения анализа и прогнозирования рынка труда применяются динамические ряды, тренды, а также алгоритмы и блок-схемы. Для начала необходимо провести анализ требований к данной модели. 2.1 Анализ ...
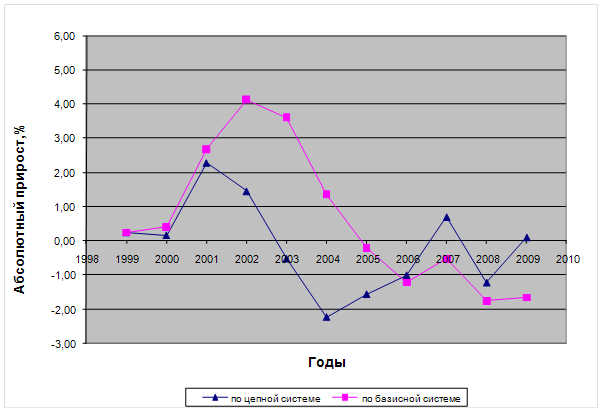
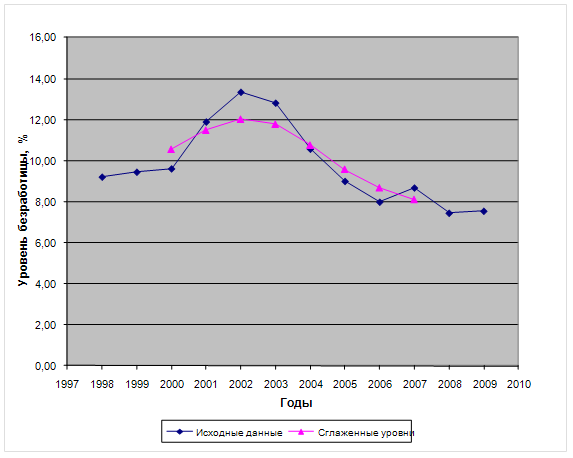
... и сельского хозяйства. Хотя и наблюдается рост средней продолжительности поисков работы, что 60-80 % трудоустраивающихся находят работу менее чем за 4 месяца 3 Статистический анализ занятости населения 3.1 Анализ динамики уровня безработицы Анализ динамики явления производится на основе рядов динамики. Ряд динамики, или временной ряд – это последовательность упорядоченных во времени ...
... полномочий; · методологическое и организационное обеспечение формирования показателей, характеризующих уровень достижения целей социально-экономического развития государства, и показателей деятельности федеральных органов исполнительной власти; · интеграцию статистических информационных ресурсов на основе методологической и технологической совместимости для эффективного их использования при ...






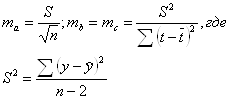
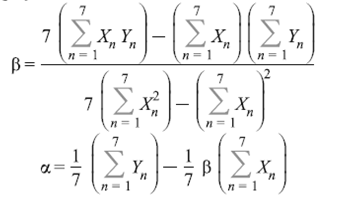
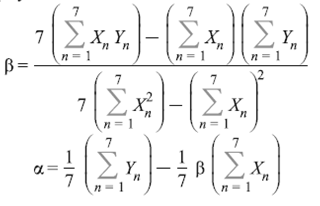
0 комментариев