Навигация
Выявление основной тенденции
4. Выявление основной тенденции.
Метод скользящей средней.
Сначала найдем скользящие средние путем суммирования уровней ряда за каждые 4 года и разделив полученные суммы на 4. Потом найдем центрированные скользящие средние, для чего найдем средние значения из 2 последовательных скользящих средних. И найдем оценки сезонной компоненты.
Таблица 6. Расчет оценок сезонной компоненты.
| Безраб-ных, тыс.чел. | Скольз. Средняя | Центр. Скол.сред | Оценка сезон комп S | |
| 1 | 48,03 | - | - | - |
| 2 | 60,06 | 67,685 | - | - |
| 3 | 66,39 | 79,075 | 73,38 | -6,99 |
| 4 | 96,26 | 85,245 | 82,16 | 14,1 |
| 5 | 93,59 | 91,875 | 88,56 | 5,03 |
| 6 | 84,74 | 88,125 | 90 | -5,26 |
| 7 | 92,91 | 82,16 | 85,143 | 7,7675 |
| 8 | 81,26 | 80,188 | 81,173 | 0,086 |
| 9 | 69,73 | 73,935 | 77,061 | -7,331 |
| 10 | 76,85 | 67,153 | 70,544 | 6,306 |
| 11 | 67,9 | - | - | - |
| 12 | 54,13 | - | - | - |
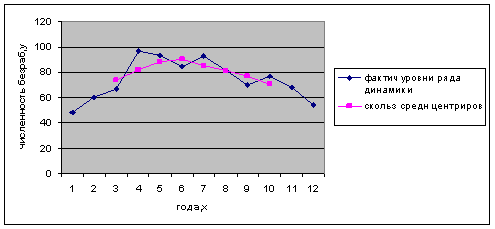
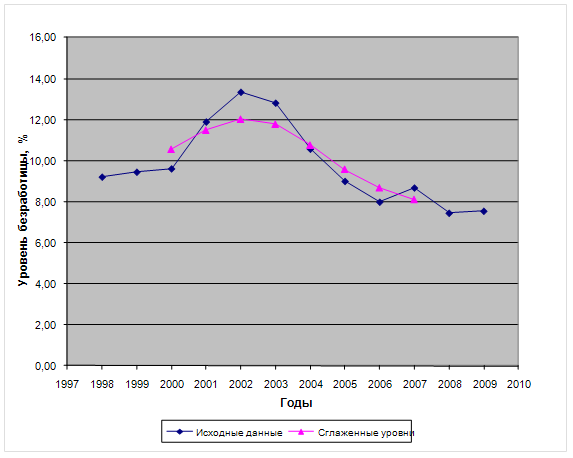
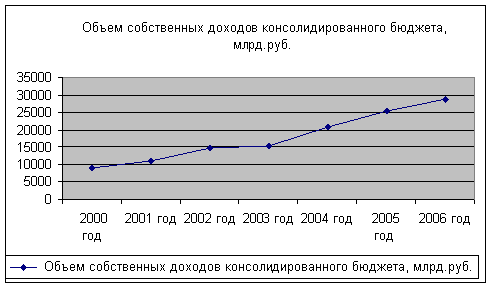
Рис. 1. Динамика численности безработных за 1994-2005гг.
Скользящая средняя дает более или менее плавное изменение уровней.
На графике не проявляется сильно выраженный недостаток скользящих средних. Но в начале и в конце динамического ряда отсутствуют данные, в результате чего становится не совсем ясна закономерность. Это и является минусом данного, наиболее простого из всех остальных метода. Для более точного анализа использую метод аналитического выравнивания.
Метод аналитического выравнивания и определение параметров.
Аналитическое выравнивание ряда динамики имеет задачу найти плановую линию развития (тренд) данного явления, характеризующую основную тенденцию её динамики.
Для отображения основной тенденции развития явления применяются полиномы разной степени, при которых оценка параметров производится по МНК. Так, для линейного тренда y=a+bt система уравнений следующая:
Таблица 7. Расчет параметров линейного тренда.
| год | тыс.чел. | t | t2 | уt |
| 1992 | 29,3 | 1 | 1 | 29,3 |
| 1993 | 29,25 | 2 | 4 | 58,5 |
| 1994 | 48,03 | 3 | 9 | 144,09 |
| 1995 | 60,06 | 4 | 16 | 240,24 |
| 1996 | 66,39 | 5 | 25 | 331,95 |
| 1997 | 96,26 | 6 | 36 | 577,56 |
| 1998 | 93,59 | 7 | 49 | 655,13 |
| 1999 | 84,74 | 8 | 64 | 677,92 |
| 2000 | 92,91 | 9 | 81 | 836,19 |
| 2001 | 81,26 | 10 | 100 | 812,6 |
| 2002 | 69,73 | 11 | 121 | 767,03 |
| 2003 | 76,85 | 12 | 144 | 922,2 |
| 2004 | 67,9 | 13 | 169 | 882,7 |
| 2005 | 54,13 | 14 | 196 | 757,82 |
| итого | 950,4 | 105 | 1015 | 7693,23 |
Из таблицы 7 подставим значения в систему и получим:
Уравнение "линейной" модели примет вид: ![]()
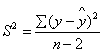 | |||||
Оценим параметры уравнения на типичность. Для расчёта используем следующие формулы:
где: S2- остаточная уточнённая дисперсия; mа, mв- ошибки по параметрам.
После подстановки значений получились следующие данные:
![]()
![]()

Оценим значимость параметров модели по критерию Стьюдента. Предположим, что параметры и коэффициент корреляции стат. значимы.
где: ta , tb- расчётное значение t-критерия Стьюдента для параметров.
После подстановки данных в формулы получим следующие значения:
![]()
![]()
![]()
Сравним полученное значение с табличным tтабличное при Р=0,05 (уровень значимости) и (n-2)= 2,1788. Так как tрасчётное > tтабличное , то параметры уравнения типичны (значимы) и данное уравнение используется в дальнейших расчетах.
Оценим уравнение в целом по критерию Фишера, выдвигаем гипотезу Н0: о том, что коэффициент регрессии равен нулю.
![]()
![]()
Fф=Dфакт/Dост=2410,54/405,25=5,95.
FT(v1=1;v2=12)=4,75.
Поскольку Fф > FT при 5%-ном уровне значимости гипотеза Н0 отвергается, уравнение в целом стат. значимо.
Из уравнения видно, что ежегодно численность безработных возрастала в среднем на 2,49%.
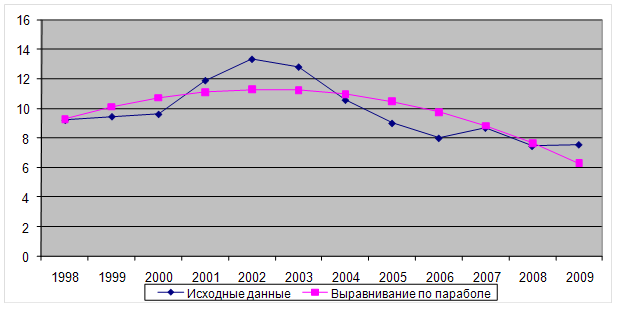
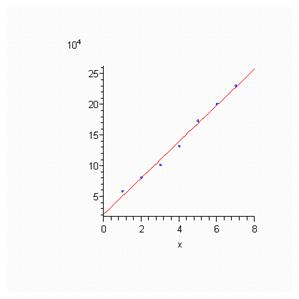
Построим график исходных данных.
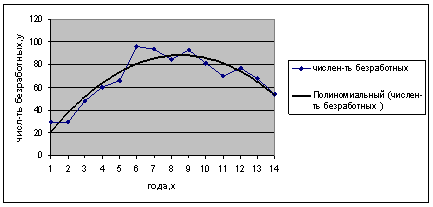
Рис. 2. График исходных данных.
По графику видно, что временной ряд характеризуется сначала тенденцией возрастания до 2000г., а затем убывания. Можно предположить, что данный ряд, вероятно, развивается согласно полиномиальной функции, которая описывается параболой второго порядка: ![]()
Система нормальных уравнений для расчета параметров параболы 2-ой степени составит:
год | тыс.чел. | t | t2 | t3 | t4 | yt | yt2 |
| 1992 | 29,3 | 1 | 1 | 1 | 1 | 29,3 | 29,3 |
| 1993 | 29,25 | 2 | 4 | 8 | 16 | 58,5 | 117 |
| 1994 | 48,03 | 3 | 9 | 27 | 81 | 144,09 | 432,27 |
| 1995 | 60,06 | 4 | 16 | 64 | 256 | 240,24 | 960,96 |
| 1996 | 66,39 | 5 | 25 | 125 | 625 | 331,95 | 1659,75 |
| 1997 | 96,26 | 6 | 36 | 216 | 1296 | 577,56 | 3465,36 |
| 1998 | 93,59 | 7 | 49 | 343 | 2401 | 655,13 | 4585,91 |
| 1999 | 84,74 | 8 | 64 | 512 | 4096 | 677,92 | 5423,36 |
| 2000 | 92,91 | 9 | 81 | 729 | 6561 | 836,19 | 7525,71 |
| 2001 | 81,26 | 10 | 100 | 1000 | 10000 | 812,6 | 8126 |
| 2002 | 69,73 | 11 | 121 | 1331 | 14641 | 767,03 | 8437,33 |
| 2003 | 76,85 | 12 | 144 | 1728 | 20736 | 922,2 | 11066,4 |
| 2004 | 67,9 | 13 | 169 | 2197 | 28561 | 882,7 | 11475,1 |
| 2005 | 54,13 | 14 | 196 | 2744 | 38416 | 757,82 | 10609,5 |
| итого | 950,4 | 105 | 1015 | 11025 | 127687 | 7693,23 | 73913,9 |
Решив систему, получим параметры уравнения тренда:
а=13,37; b=13,94; c=-1,0017.
Соответственно уравнение тренда составит: у =13,37+13,94t-1,0017t2
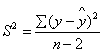 | |||||
Оценим параметры уравнения на типичность.
где: S2- остаточная уточнённая дисперсия; mа, mв, mr - ошибки по параметрам.
После подстановки значений получились следующие данные:
![]()
![]()
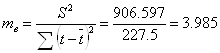
![]()
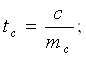 | |||||||
Оценим значимость параметров модели по критерию Стьюдента.
Предположим, что параметры и коэффициент корреляции стат.
значимы. Для расчёта использую следующие формулы:
где: ta , tb , tr - расчётное значение t-критерия Стьюдента для параметров.
После подстановки данных в формулы получил следующие значения:
![]()
![]()
![]()
![]()
Сравним полученное значение с табличным t-критерием Стьюдента. tтабличное при Р=0,05 и (n-2)= 2,1788. Так как tрасчётное > tтабличное , то параметры b и r уравнения типичны (значимы). Так как tрасчётное < tтабличное , то параметры с и а незначимы.
Оценим уравнение в целом по критерию Фишера, выдвигаем гипотезу Н0:о том, что коэффициент регрессии равен нулю.
Fф=Dфакт/Dост=10333,6/906,597=11,398.
FT(v1=1;v2=12)=4,75.
Т.к. Fф > FT при 5%-ном уровне значимости гипотеза Н0 отвергается, уравнение в целом стат. значимо.
Похожие работы
... степень сбалансированности системы подготовки кадров с потребностью экономики в квалифицированных работниках. 6.2. Статистика занятости и безработицы Занятость - одна из важнейших социально-экономических проблем рыночной экономики. Ее статистическое отражение неоднократно обсуждалось на международных конференциях статистиков труда (1949, 1957, 1982, 1993 гг.), проводимых Международным бюро ...
... с распространением явления неполная занятость: , (1.11) где ТНЗ– численность занятых неполное рабочее время [1]. 2 ПРОЕКТНАЯ ЧАСТЬ В курсовом проекте для проведения анализа и прогнозирования рынка труда применяются динамические ряды, тренды, а также алгоритмы и блок-схемы. Для начала необходимо провести анализ требований к данной модели. 2.1 Анализ ...
... и сельского хозяйства. Хотя и наблюдается рост средней продолжительности поисков работы, что 60-80 % трудоустраивающихся находят работу менее чем за 4 месяца 3 Статистический анализ занятости населения 3.1 Анализ динамики уровня безработицы Анализ динамики явления производится на основе рядов динамики. Ряд динамики, или временной ряд – это последовательность упорядоченных во времени ...
... полномочий; · методологическое и организационное обеспечение формирования показателей, характеризующих уровень достижения целей социально-экономического развития государства, и показателей деятельности федеральных органов исполнительной власти; · интеграцию статистических информационных ресурсов на основе методологической и технологической совместимости для эффективного их использования при ...






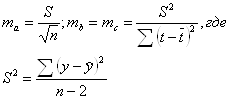
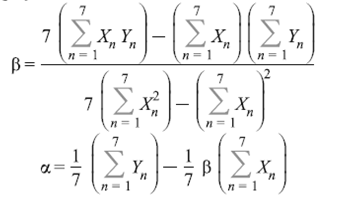
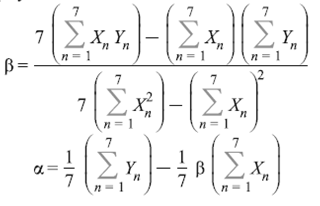
0 комментариев