Навигация
Линейные регрессионные модели
Используя данные Федеральной службы государственной статистики России (за двенадцать месяцев) из периода 2004 - 2005гг., следует:
1. Оценить влияние факторов (X1, X2, X3, X4, X5, X6, X7, X8) на изучаемый показатель (Y) и друг на друга с помощью коэффициентов линейной корреляцииТаблица 1.
| в% к предыдущему периоду | индексы цен платных услуг | индексы цен производителей | добыча полезных ископаемых | обрабатывающие производства | производство и распределение электроэнергии газа и воды | индексы тарифов на грузовые перевозки | железнодорожный транспорт | автомобильный транспорт | трубопроводный транспорт |
|
| Y | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 |
| ицпу | пр | дпи | оп | прэгв | гп | жт | ат | тт | |
| июл.04 | 101,3 | 101,2 | 102,9 | 100,7 | 100,1 | 102,1 | 100 | 101,3 | 105 |
| авг.04 | 101 | 101,8 | 103,9 | 101,4 | 100,2 | 100,2 | 100 | 100,4 | 100 |
| сен.04 | 100,6 | 103,1 | 105 | 103,1 | 100 | 100,3 | 100 | 101,9 | 100,6 |
| окт.04 | 101,2 | 101,8 | 103,6 | 101,4 | 99,9 | 95,4 | 100 | 101,5 | 87,4 |
| ноя.04 | 100,8 | 102 | 104,5 | 101,5 | 100 | 100,7 | 100 | 101,9 | 101,1 |
| дек.04 | 101 | 100,1 | 100,8 | 99,8 | 99,9 | 102,1 | 100 | 100,6 | 105,8 |
| янв.05 | 108,8 | 100,5 | 95,7 | 100,9 | 104,9 | 113,9 | 108,8 | 103,2 | 122,6 |
| фев.05 | 102,2 | 101,3 | 98,4 | 100,9 | 106,3 | 100,1 | 100 | 100,8 | 100,1 |
| мар.05 | 101,2 | 102,5 | 109,6 | 101 | 100,3 | 100 | 100 | 100,3 | 99,9 |
| апр.05 | 100,8 | 102,5 | 108,9 | 101,1 | 100,3 | 103,5 | 100 | 101 | 107,7 |
| май.05 | 100,8 | 102,7 | 109,7 | 101 | 100,1 | 100,3 | 100 | 100,5 | 100 |
| июн.05 | 100,9 | 100,1 | 99,3 | 100,3 | 100,1 | 101,7 | 100 | 100,6 | 103,7 |
Коэффициент линейной корреляции, с помощью которого можно оценить влияние факторов (X1, X2, X3, X4, X5, X6, X7, X8) на изучаемый показатель (Y) и друг на друга, вычисляется по формуле:
![]() ,
,
где ![]() - среднее квадратическое отклонение фактора
- среднее квадратическое отклонение фактора ![]() .
.
![]() - среднее квадратическое отклонение изучаемого показателя
- среднее квадратическое отклонение изучаемого показателя ![]() . Если
. Если ![]() =0, то факторы не могут влиять на изучаемый показатель, так как связь между ними будет отсутствовать. Чем ближе
=0, то факторы не могут влиять на изучаемый показатель, так как связь между ними будет отсутствовать. Чем ближе ![]() к 1, тем сильнее связь между факторами и изучаемым показателем. Рассмотрим сначала как влияет X1 на изучаемый показатель Y. Произведем предварительные расчеты в таблице:
к 1, тем сильнее связь между факторами и изучаемым показателем. Рассмотрим сначала как влияет X1 на изучаемый показатель Y. Произведем предварительные расчеты в таблице:
Таблица 2.
| |
|
|
|
| |
| июл.04 | 101,3 | 101,2 | 10251,56 | 10261,69 | 10241,44 |
| авг.04 | 101 | 101,8 | 10281,8 | 10201 | 10363,24 |
| сен.04 | 100,6 | 103,1 | 10371,86 | 10120,36 | 10629,61 |
| окт.04 | 101,2 | 101,8 | 10281,6 | 10241,44 | 10363,24 |
| ноя.04 | 100,8 | 102 | 10281,6 | 10160,64 | 10404 |
| дек.04 | 101 | 100,1 | 10110,1 | 10201 | 10020,01 |
| янв.05 | 108,8 | 100,5 | 10934,4 | 11837,44 | 10100,25 |
| фев.05 | 102,2 | 101,3 | 10352,86 | 10444,84 | 10261,69 |
| мар.05 | 101,2 | 102,5 | 10373 | 10241,44 | 10506,25 |
| апр.05 | 100,8 | 102,5 | 10332 | 10160,64 | 10506,25 |
| май.05 | 100,8 | 102,7 | 10352,16 | 10160,64 | 10547,29 |
| июн.05 | 100,9 | 100,1 | 10100,09 | 10180,81 | 10020,01 |
| Сумма | 1220,6 | 1219,6 | 124023,03 | 124211,94 | 123963,3 |
| Среднее значение | 101,71667 | 101,6333 | 10336,96666 | 10350,995 | 10330,27 |
![]()
Из таблицы находим среднее квадратическое отклонение фактора ![]() :
:
![]() =
=![]() =0,9679876;
=0,9679876;
среднее квадратическое отклонение изучаемого показателя ![]() :
:
![]() =
=![]() =2,1718655.
=2,1718655.
Полученные значения подставляем в формулу:
![]() =
=![]() =-0,41056
=-0,41056
Коэффициент линейной корреляции равен 0,3 ≤ ![]() =
=![]() ≤0,7. Это говорит о том, что связь между изучаемым показателем (Y) и фактором
≤0,7. Это говорит о том, что связь между изучаемым показателем (Y) и фактором ![]() умеренная.
умеренная.
Аналогично оценивается влияние остальных факторов на изучаемый показатель (Y).
![]() =
=![]()
Коэффициент линейной корреляции равен 0,3 ≤ ![]() =
=![]() ≤0,7. Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х2 умеренная.
≤0,7. Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х2 умеренная.
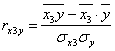 =
=![]()
![]()
Коэффициент линейной корреляции равен ![]() =
=![]() < 0,3. Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х3 слабая.
< 0,3. Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х3 слабая.
![]() =
=![]()
![]()
Коэффициент линейной корреляции равен 0,3 ≤ ![]() =
=![]() ≤0,7. Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х4 умеренная.
≤0,7. Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х4 умеренная.
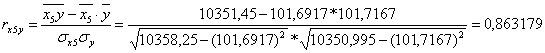
Коэффициент линейной корреляции равен 0,7 < ![]() =
=![]() Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х5 близка к линейной (тесная).
Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х5 близка к линейной (тесная).
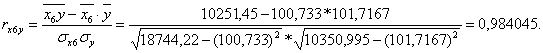
Коэффициент линейной корреляции равен 0,7 < ![]() =
=![]() Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х6 близка к линейной (тесная).
Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х6 близка к линейной (тесная).
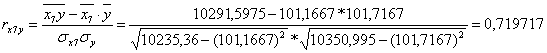
Коэффициент линейной корреляции равен 0,7 < ![]() =
=![]() Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х7 близка к линейной (тесная).
Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х7 близка к линейной (тесная).
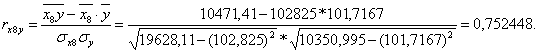
Коэффициент линейной корреляции равен 0,7 < ![]() =
=![]() Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х8 близка к линейной (тесная).
Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х8 близка к линейной (тесная).
Влияние факторов друг на друга рассчитывается аналогично. Все полученные данные представим в таблице.
Таблица 3.
| Y | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | |
| Y | 1 | ||||||||
| X1 | -0,41056 | 1 | |||||||
| X2 | -0,62049 | 0,817335 | 1 | ||||||
| X3 | -0,14167 | 0,750202 | 0,304572 | 1 | |||||
| X4 | 0,684791 | -0,31544 | -0,63666 | -0,13627 | 1 | ||||
| X5 | 0,863179 | -0,39974 | -0,4795 | -0,21126 | 0,494364 | 1 | |||
| X6 | 0,984045 | -0,36981 | -0,55741 | -0,09167 | 0,560132 | 0,89804 | 1 | ||
| X7 | 0,719717 | -0,08272 | -0,45151 | 0,36154 | 0,360766 | 0,610648 | 0,762909 | 1 | |
| X8 | 0,752448 | -0,40384 | -0,42926 | -0,26069 | 0,440197 | 0,978356 | 0,790727 | 0,493109 | 1 |
Из свойств корреляции известно, что если ![]() > 0, то связь прямая (
> 0, то связь прямая (![]() ); если
); если ![]() < 0, то связь обратная
< 0, то связь обратная ![]() ). Факторы (Х1), (Х3), (Х2) имеют обратную связь с ицпу, то есть если индекс цен платных услуг растет, они падают, и наоборот. Факторы (Х4), (Х5), (Х6), (Х7), (Х8) имеют прямую связь с индексом цен платных услуг (вместе с ним растут или падают).
). Факторы (Х1), (Х3), (Х2) имеют обратную связь с ицпу, то есть если индекс цен платных услуг растет, они падают, и наоборот. Факторы (Х4), (Х5), (Х6), (Х7), (Х8) имеют прямую связь с индексом цен платных услуг (вместе с ним растут или падают).
Самая сильная связь наблюдается между индексом цен платных услуг и железнодорожным транспортом. Самая слабая связь наблюдается между обрабатывающим производством и производством и распределением электроэнергии, газа и воды.
2. Используя процедуру выбора факторов, предложить и построить линейные регрессионные модели изучаемого показателя. Оценить качество моделей
При процедуре выбора факторов должны выполняться следующие условия:
Факторы должны быть количественно измеримы или допускать кодировку. В нашем случае это условие выполняется.
Факторы должны "объяснять" поведение изучаемого показателя согласно принятым положениям экономической теории. Это должно подтверждаться индексами корреляции факторов с показателями. Это условие тоже выполняется, так как для всех факторов индексы корреляции рассчитаны.
Факторы не должны находиться в точной функциональной связи (допустим, коллинеарной). Включение в модель факторов с индексами корреляции, близкими по модулю к единице может привести к нежелательным последствиям:
1) факторы будут дублировать друг друга, и будет затруднена экономическая интерпретация параметров модели;
2) система уравнений для определения параметров может оказаться плохо обусловленной и повлечь ненадежность полученных уравнений регрессии т нежелательность их использования для анализа и прогноза.
При наличии корреляции ≥0,7 между факторами один из них следует исключить. Оставить рекомендуется тот, который при достаточно тесной связи с показателем имеет более слабую связь с другими факторами.
Рассмотрим таблицу 3, используя метод исключения, отберем факторы для построения регрессионных моделей. Так как связь между факторами должна быть слабой, исключим все факторы, коэффициент корреляции которых больше или равен по модулю 0,3. Для построения модели оставляем факторы сильно или умеренно влияющие на данный показатель, то есть коэффициент корреляции должен быть больше или равен 0,3.
Следующее необходимое условие при построении регриссионных моделей: Число включаемых факторов должно в 6 раз меньше объема наблюдений, по которым строится регрессия. N-число наблюдений в нашем случае равно 12. Тогда m ≤ ![]() , то есть m=1 или m=2.
, то есть m=1 или m=2.
Число параметров при факторах в линейной модели совпадают с их количеством: m=p.
Итак, можно предложить следующие регрессионные модели:
1. ![]()
2. ![]() .
.
3. ![]() .
.
Используя инструмент РЕГРЕССИЯ, оценим 1 модель.
Похожие работы
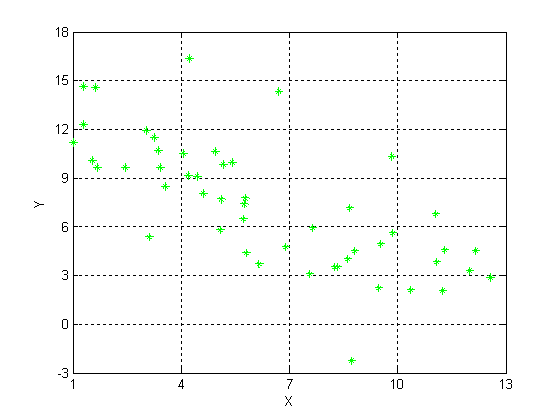
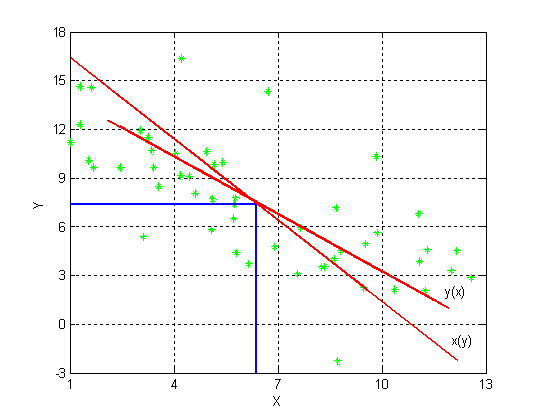
... , ; , , ; Случай группированных данных. Подставим найденные значения в уравнеиня линейной регрессии Y на x и X на y. Получим: y(x) = 17,14 – 1,4*x; x(y) = 10,83 – 0,54*y; Проверка: Задание 5 Для негруппированных данных нанести графики выборочных регрессионных прямых на диаграмму рассеивания. Задание 6 Для негруппированных данных по найденным оценкам параметров ...
... теперь на основе выше рассчитанного доверительный интервал: 3.Сравнительный анализ расчетов, произведенных с помощью формул Excel и с использованием «Пакета анализа» Если сравнивать между собой результаты, полученные при расчетах линейной и степенной регрессионной модели, то можно выделить следующее: 1. Значение b1 в линейной регрессионной модели < b1 в степенной регрессионной ...
... 9472;───────┴─────────┘ Реализация алгоритма многомерного регрессионного анализа начинается с расчета важнейших статистических характеристик исходной информации и матрицы выборочных парных коэффициентов корреляции. Рассмотрим более подробно вариационные характеристики переменной у: ...
... деле независимой постоянной составляющей в отклике нет (альтернатива – гипотеза Н1: a ¹ 0). Для проверки этой гипотезы, с заданным уровнем значимости g, рассчитывается t-статистика, для парной регрессии: Значение t-статистики сравнивается с табличным значением tg/2(n-1) - g/2-процентной точка распределения Стьюдента с (n-1) степенями свободы. Если |t| < tg/2(n-1) – гипотеза Н0 не ...
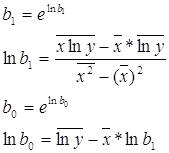
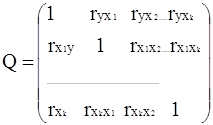
0 комментариев