Навигация
Этап. Оценка значимости модели в целом
1 этап. Оценка значимости модели в целом.
Таблица 7.
| ВЫВОД ИТОГОВ | |||||
| Регрессионная статистика | |||||
| Множественный R | 0,863178866 | ||||
| R-квадрат | 0,745077754 | ||||
| Нормированный R-квадрат | 0,71675306 | ||||
| Стандартная ошибка | 1,263784889 | ||||
| Наблюдения | 11 | ||||
| Дисперсионный анализ | |||||
|
| df | SS | MS | F | Значимость F |
| Регрессия | 1 | 42,01290252 | 42,0129 | 26,30488273 | 0,000620555 |
| Остаток | 9 | 14,37437021 | 1,597152 | ||
| Итого | 10 | 56,38727273 | |||
| Модель линейной регрессии с фактором X5 значима в целом согласно F-критерию (F=26,304) с приемлемым уровнем значимости 0,0000000468 ≤ 0,05 Итак, получаем модель
| |||||
|
| Коэф-ты | Станд. ошибка | t-стат. | P-Значение | Нижние 95% |
| Y-пересечение | 55,68196551 | 8,991138974 | 6, 192982 | 0,00016021 | 35,34258057 |
| Х5 | 0,453226954 | 0,088368512 | 5,128829 | 0,000620555 | 0,253323338 |
Согласно критерию Стьюдента 2 параметра модели a=55,68 и b=0,453 значимы с приемлемыми уровнями ![]() <0,05 и
<0,05 и ![]() <0,05.
<0,05.
Похожие работы
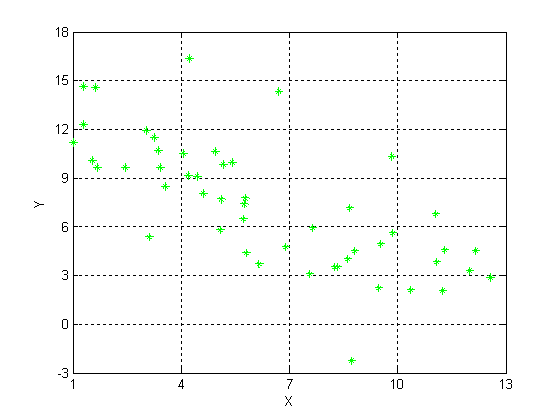
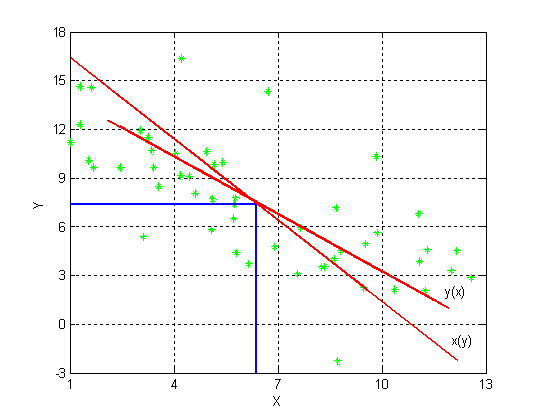
... , ; , , ; Случай группированных данных. Подставим найденные значения в уравнеиня линейной регрессии Y на x и X на y. Получим: y(x) = 17,14 – 1,4*x; x(y) = 10,83 – 0,54*y; Проверка: Задание 5 Для негруппированных данных нанести графики выборочных регрессионных прямых на диаграмму рассеивания. Задание 6 Для негруппированных данных по найденным оценкам параметров ...
... теперь на основе выше рассчитанного доверительный интервал: 3.Сравнительный анализ расчетов, произведенных с помощью формул Excel и с использованием «Пакета анализа» Если сравнивать между собой результаты, полученные при расчетах линейной и степенной регрессионной модели, то можно выделить следующее: 1. Значение b1 в линейной регрессионной модели < b1 в степенной регрессионной ...
... 9472;───────┴─────────┘ Реализация алгоритма многомерного регрессионного анализа начинается с расчета важнейших статистических характеристик исходной информации и матрицы выборочных парных коэффициентов корреляции. Рассмотрим более подробно вариационные характеристики переменной у: ...
... деле независимой постоянной составляющей в отклике нет (альтернатива – гипотеза Н1: a ¹ 0). Для проверки этой гипотезы, с заданным уровнем значимости g, рассчитывается t-статистика, для парной регрессии: Значение t-статистики сравнивается с табличным значением tg/2(n-1) - g/2-процентной точка распределения Стьюдента с (n-1) степенями свободы. Если |t| < tg/2(n-1) – гипотеза Н0 не ...
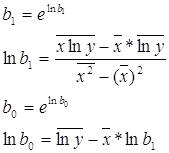
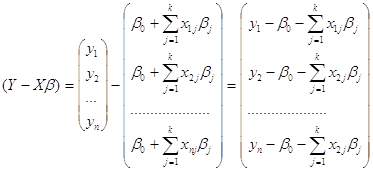
0 комментариев