Основные теоремы теории вероятностей
Локальная формула Муавра-Лапласа
Дисперсия ДСВ и ее свойства
Дифференциальная функция распределения и ее свойства
Математическое ожидание
Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции
Понятие и виды статистических гипотез
Особенности статистического анализа количественных и качественных показателей
Определение вариационных рядов. Графическое изображение вариационных рядов
Проверка адекватности модели регрессии
Концепция Data Mining
Понятие и модели дисперсионного анализа
Навигация
Проверка адекватности модели регрессии
О теории вероятностей
70295
знаков
2
таблицы
1
изображение
39. Проверка адекватности модели регрессии
После построения уровня регрессии возникает вопрос о качестве решения.
Пусть при исследовании n пар наблюдений (хi, уi) получено уравнение регрессии У на Х.
`yi = a + bxi
Рассмотрим тождество:
yi - `yi = yi - `yi – (`yi -`yi)
Если переписать это уравнение в виде
(yi-`y) = (`yi-`y) + (yi-`y)
возвести обе части в квадрат и просуммировать по i, то получим
S(yi-`y)2 =S (`yi-`y)2 + S(yi-`y)2 (*)
Уравнение (*) является основополагающим в дисперсионном анализе.
Для сумм обычно вводятся названия:
Syi2 – нескорректированная сумма квадратов У-ков;
- коррекция на среднее суммы квадратов У-ков.
-сумма квадратов отношений относительно среднего наблюдений.
S (`yi-`y)2- сумма квадратов относительно регрессии.
S(yi-`yi)2 – сумма квадратов обусловленная регрессией.
40. Интервальные оценки. Доверительная вероятность, доверительный интервал
Интервальной называют оценку, которая определяется 2 числами – границами интервала. Она позволяет ответить на вопрос: внутри какого интервала и с какой вероятностью находится неизвестное значение оцениваемого параметра генеральной совокупности. Пусть θ точечная оценка параметра θ. Чем меньше разность θ - θ , тем точнее и лучше оценка. Обычно говорят о доверительной вероятности p = 1-α, с которой θ будет находиться в интервале θ-Δ < θ < θ+Δ, где: Δ (Δ > 0) – предельная ошибка выборки, которая может быть либо задана наперед, либо вычислена; a - риск или уровень значимости (вероятность того, что неравенство будет неверным). В качестве 1-a принимают значения 0,90;0,95;0,99;0,999. Доверительная вероятность показывает, что в (1-a) 100% случаев оценка будет накрываться указанным интервалом. Для построения доверительного интервала параметра а – математического ожидания нормального распределения, составляют выборочную характеристику (статистику), функционально зависимую от наблюдений и связанную с а, например, для повторного отбора:
Статистика u распределена по нормальному закону распределения с математическим ожиданием а = 0 и средним квадратическим отклонением s = 1. Отсюда
P(|u|<u a/2)= 1-s или 2Ф(ua/2)=1-s,
где Ф-функция Лапласа, ua/2 – квантиль нормального закона распределения, соответствующая уровню значимости a.
Определение доверительного интервала для средней и доли при случайном обороте. Определение доверительного интервала для средней и доли при типическом обороте;. Определение необходимой численности выборки. Распространение данных выборки на генеральную совокупность).
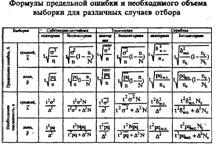
Где:
1) t— квантиль распределения соответствующая уровню значимости
:
а) при n 
30 t=
- квантиль нормального закона распре деления,
б) при n<30t - квантиль распределения Стьюдента с v=n-1 степенями свободы для двусторонней области;
2) 
- выборочная дисперсия:
а) при n30 можно считать, что
б) при n<30 вместо берут исправленную выборочную дисперсию
S2 (
)
далее везде рассматривается исправленная выборочная дисперсия S2;
З) рq — дисперсия относительной частоты в схеме повторных независимых испытаний;
4) N — объем генеральной совокупности;
5) n — объем выборки;
6) 
— средняя арифметическая групповых дисперсий (внутригрупповая дисперсия);
7) 
— средняя арифметическая дисперсий групповых долей,
8) 
— межсерийная дисперсия,
9) pqм.с. — межсерийная дисперсия доли;
10) Nc — число серий в генеральной совокупности;
11) nc — число отобранных серий (объем выборки);
12) 
— предельная ошибка выборки.
41. Статистические критерии проверки гипотез, уровень значимости и мощность критерия. Выбор м/у гипотезами Н0 и Н1 может сопровождаться ошибками 2 родов. Ошибка первого рода a означает вероятность принятия Н1, если верна гипотеза
Н0: a=Р(Н1/Н0)
Ошибка второго рода b означает вероятность принятия Н0 если верна гипотеза
Н1: b=Р(Н0/Н1)
Существует правильное решение двух видов
Р(Н0/Н0) = 1-a и Р(Н1/Н1)=1-b.
Правило, по которому принимается решение о том, что верна или неверна гипотеза Н0 называется критерием, где:
a=Р(Н1/Н0)
уровень значимости критерия;
М= Р(Н1/Н1)=1-b
мощность критерия. Статистический критерий К – случайная величина, с помощью которой принимают решение о принятии или отклонении Н0.
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...
0 комментариев