Навигация
Дифференциальная функция распределения и ее свойства
15. Дифференциальная функция распределения и ее свойства
СВ X непрерывна, если ее интегральная функция непрерывна на всей числовой оси. СВ X непрерывна и имеет дифференциальную функцию, если ее интегральная функция непрерывна и дифференцируема всюду, за исключением конечного числа точек на любом конечном промежутке.
Дифференциальной функцией (функцией плотности вероятности) СВ X называется производная ее функции распределения: f(x)=F'(x).
С помощью дифференциальной функции можно получить формулу вероятности попадания СВ X в заданный интервал:
![]()
Свойства дифференциальной функции:
). f(x)≥0;
![]()
![]()
16. Числовые характеристики непрерывных случайных величин
1) Математическое ожидание НСВ X определяется по формуле
М(Х)= ∫xf(x)dx. (2.7.1)
Если НСВ X определена на интервале (а; b), то
М(Х)= ∫xf(x)dx.
2) Мода НСВ X будет определяться как максимум ее дифференциальной функции: Мо(Х) = max f (x).
3) Медиана определяется как значение случайной величины, которое делит площадь под дифференциальной функцией на две равные части. Me(X): P(x<Me(X))=P(x>Me(X))=1/2.
4). Дисперсия НВС
![]()
Все св-ва дисперсии и мат-го ожидания, установленные для ДСВ, сохраняется для НСВ.
Замечание. Если распределение симметрично, то его мода, медиана и математическое ожидание совпадают.
5). Моменты случайных величин.
Кроме характеристик положения и рассеяния существует ряд других числовых характеристик распределения, например, моменты.
Начальным моментом порядка s называется математическое ожидание степени s CB X: αs=M(Xs).
Для ДСВ:
![]()
![]()
При s=l:α1, = M(X) = mx, то есть, первый начальный момент - это математическое ожидание СВ.
Отклонение СВ от ее математического ожидания называется центрированной СВ X: X = Х-mх.
Центральным моментом порядка s СВ X называется математическое ожидание степени s, соответствующей центрированной СВ: μs=μ(Xs)=M((x-M(X))s).
![]()
![]()
При вычислении центральных моментов пользуются формулами связи между центральными и начальными моментами:
μ1=0,
μ2=α2-m2x,
μ3=α3-3mxα2+2m3x,
μ4=α4-4mxα3+6m2xα2-3m4x.
Обычно рассматривают первые четыре центральных момента:
1). μ1=M(x-mx)=0 – мат-ое ожидание центрированной СВ равно нулю;
2). μ2= M(x-mx)2=D(X) – второй центральный момент – это дисперсия;
3). μ3= M(x-mx)3- третий центральный момент может служить для характеристики асимметрии, обычно рассматривают безразмерный коэффициент асимметрии
Sk=μ3/σ3.
4). Четвёртый центральный момент
μ4=M(x-mx)4,
может служить для характеристики “крутости” или островершинности распределения, описывающиеся с помощью эксцесса:
Ex=(μ4/σ4)-3.
Основным моментом порядка s называется нормированный центральный момент порядка s:
rs= μs/σs, то есть Sk=r3, Ex=r4-3
17. Равномерный закон распределения
СВ X распределена по равномерному (прямоугольному) закону, если все значения СВ лежат внутри некоторого интервала и все они равновероятны (точнее обладают одной плотностью вероятности).Например, если весы имеют точность 1г и полученное значение округляется до ближайшего целого числа k, то точный вес можно считать равномерно распределенной СВ на интервале (k-0,5; k+0,5).
Дифференциальная функция равномерного закона на интервале (α,β) (рис. 11):

Интегральная функция равномерного закона на интервале (α,β) (рис. 11):
![]()

Рис. Дифференциальная функция
2). Интегральная функция.
Основные числовые характеристики равномерного закона:
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...





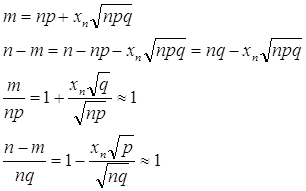
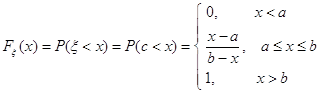
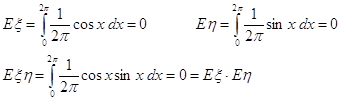
0 комментариев