Навигация
Определение вариационных рядов. Графическое изображение вариационных рядов
31. Определение вариационных рядов. Графическое изображение вариационных рядов
В реальных социально-экономических системах нельзя проводить эксперименты, поэтому данные обычно представляют собой пассивные наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений, в общем случае, ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжировать).
Операция, заключенная в расположении значений признака по не убыванию, называется ранжированием опытных данных.
После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (хi). Число элементов в каждой группе называется частотой варианта (ni).
Размахом выборки называется число
W=xmax- х min,
где xmax - наибольший вариант, х min - наименьший вариант.
Сумма всех частот равна определенному числу n, которое называется объемом совокупности:
![]()
Отношение частоты данного варианта к объему совокупности называется относительной частотой (pi) или частостью этого варианта: pi=ni/n.
![]()
Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация - изменение).
Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.
Построение дискретного вариационного ряда нецелесообразно, если число значений признака велико или признак является непрерывным, то есть может принимать любые значения в пределах некоторого интервала. В этом случае следует построить интервальный вариационный ряд. Для построения такого ряда промежуток изменения признака разбивается на ряд отдельных интервалов и подсчитывается количество значений величины в каждом из них.
Будем считать, что отдельные (частичные) интервалы имеют одну и ту же длину. Число интервалов (k), в случае нормально распределённой совокупности, можно определить по формуле Стерджесса k = l +3,3221g n. или приближённо: k [6;12]. Длина частичного интервала определяется по формуле
![]()
Графическое изображение вариационных рядов.
Вариационные ряды изображают графически с помощью полигона и гистограммы.
Полигон частот - это ломаная, отрезки которой соединяют точки (x1; n1), (x2;n2),... (хk;nk).
Полигон относительных частот - это ломаная, отрезки которой соединяют точки
![]()
Гистограммой частот называется фигура, состоящая из прямоугольников с основанием h и высотами ni. Для гистограммы относительных частот в качестве высоты рассматривают ni/n. Гистограмма относительных частот является аналогом дифференциальной функции случайной величины.

Рис. Гистограмма частот
32. Общие модели статистического анализа
Характеристика методов многомерного анализа, (компонентный анализ, факторный анализ, кластер-анализ(классификация без обучения). Дискриминантный анализ (классификация с обучением. Канонические корреляции. Множественный ковариационный анализ).
Реальные процессы зависят от параметров, их характеристик, поэтому возникает необходимость в применении мер, методов статистического анализа.
Методы МСА следует рассматривать, как логическое продолжение методов ТВ и МС. Принципиальное различие состоит в учете более 3-х факторов.
Методы МСА базируются на представлении информации в многомерном пространстве и позволяют определить латентные зак-ти, сущ-ие объективно.
Методы:
- моделирования и первичной обработки данных
- анализа и построения зависимости
- классификация и снижение зависимости размерности
33. Средняя арифметическая ряда
Вариационные ряды позволяют получить первое представление об изучаемом распределении. Далее необходимо исследовать числовые характеристики распределения (аналогичные характеристикам распределения теории вероятностей): характеристики положения (средняя арифметическая, мода, медиана); характеристики рассеяния (дисперсия, среднее квадратическое отклонение, коэффициент вариации); характеристики меры скошенности (коэффициент асимметрии) и островершинности (эксцесс) распределения.
Средней арифметической (х) дискретного вариационного ряда называется отношение суммы произведений вариантов на соответствующие частоты к объему совокупности:
![]() (3.2.1)
(3.2.1)
Модой (М*(Х)) дискретного вариационного ряда называется вариант, имеющий наибольшую частоту.
Медианой (М*(Х)) дискретного вариационного ряда называется вариант, делящий ряд на две равные части. Если дискретный вариационный ряд имеет 2n членов: x1, x2, ..., xn, xn+1, ... x2n, то
Ме*(Х)=(xn+xn+1)/2.
Если дискретный вариационный ряд имеет 2n+1 членов: x1, x2, ..., xn-1, xn, xn+1, ... x2n+1, то
М*e(Х)=xn+1.
Для интервальных вариационных рядов (с равными интервалами для медианы и моды) имеют место формулы: а) медианы
![]()
где хМе - начало медианного интервала, h - длина частичного интервала, n - объем совокупности, SMe-i, - накопленная частота интервала, предшествующего медианному, nМе -частота медианного интервала;
б) моды
![]()
где хМо- начало модального интервала, h -длина частичного интервала, nмо - частота модального интервала, nМо-1 -частота предмодального интервала, nМо+1 - частота послемодального интервала;
в) средней арифметической, совпадающей с формулой (3.2.1) для дискретного вариационного ряда, причем в качестве вариант хi принимаются середины соответствующих интервалов (интервалы могут иметь как одинаковую, так и разную длину).
Мода и медиана используются в качестве характеристики среднего положения в случае, если границы ряда нечеткие или если ряд не симметричен.
34. Проблема размерностей в многомерных методах исследования
Метод МСА базируется на представлении данных в многомерном признаковом пространстве размерностью, равной числу признака. При этом исследователь часто сталкивается с понятием размерности.
В общем случае изучается n-мерное эвклидово пространство. При n>3 все задачи решаются только логически и алгебраически (n>>m) (m=2-3). Для этого обычно стараются снизить размерность изучаемого пространства без видимых потерь информации.
Основные предпосылки перехода к производству меньшей размерности.
1. дублирование информации
2. ненормативность признаков
3. возможность агрегирования (простого или взвешенного суммирования)
Основной минус МСА: статистические методы оценивания и сравнения основываются только на многомерном нормальном законе раск-ния.
35. Введение в Excel
Табулирование – вычисление значений функций, при известных значениях аргумента.
БД – это фактически любой набор данных. Создание баз данных упрощает обработку данных и их анализ.
Группировка – разбиение на группы, удовлетворяющие определенным критериям
Можно для облегчения работы с данными использовать Пакет анализа содержащий 13 категорий функций:
Финансовые (51 функция)
Дата и время (19 функций)
Математические (60)
Пользовательские (11-при сложных вычислениях)
Логические (6)
Статистические (самая объемная - 78)
Ссылки и массивы
Информационные и тд.
36. Современные пакеты прикладных программ МС исследования. Пакет статистика. Стандарт качества ISO 9000. Система SEWS применение многомерных статистических методов в социально экономических исследованиях
За 200 лет математиками, экономистами, психологами был создан аппарат принятия решений, которых называется МС, а позже прикладной С или анализом данных
Широкому внедрению методов анализа данных в 60-70гг. способствовало появление компонентов, причем если до середины 80г. Эти методы рассматривались, как инструмент научных исследований, то теперь основными показателями стали компоненты организации и тд.
Пакет statistika версия stat 5.5 русскоязычная поддержка всех архитектур документация 3000с.
1. иногда слишком поверхностны
2. неудобный редактор отсчета
3. высокая стоимость
37. Дисперсия дискретного ряда
Дисперсия дискретного ряда распределения:
![]()
характеризует средний квадрат отклонения х от х---,
Среднее квадратическое отклонение дискретного ряда распределения:
![]()
выражается в тех же единицах, что и хi.
Коэффициент вариации:
![]()
характеризует относительное значение среднего квадратического отклонения и обычно служит для сравнения колеблемости несоизмеримых показателей.
Если объединяются несколько распределений в одно, то общая дисперсия σ0*2 нового распределения равна средней арифметической из дисперсий объединяемых распределений, сложенной с дисперсией частных средних относительно общей средней нового распределения:
![]()
где x0-- - средняя ариф-кая нового распределения, xi-- - средняя ариф-кая i–го частного распределения (I=1,…,k).
n - объем i-гo частного распределения, хij - j-й член i-го частного распределения (j=l,..., ni; i=l,2,..., к), δ*2 -
межгрупповая дисперсия, --σ*2 - внутригрупповая дисперсия, N=∑ni - объем нового распределения.
Значения --σ*2 и δ*2 определяются по формулам
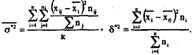
Дисперсия имеет важное свойство, заключающееся в том, что
D*=(∑(xi-d)2ni)/k принимает наименьшее значение при d=--x.
38. Моменты для вариационных рядов в математической статистике находятся по формулам, аналогичным формулам (2.7.6), (2.7.7)>(2.7.11), (2.10.3):
![]() - начальный момент s–го порядка,
- начальный момент s–го порядка,
![]() - центральный момент s–го порядка.
- центральный момент s–го порядка.
![]() - основной момент s-гo порядка
- основной момент s-гo порядка
![]() - основной момент порядка s, h.
- основной момент порядка s, h.
Соотношения между начальными и центральными моментами в математической статистике соответствуют формулам (2.7.8).
Коэффициент асимметрии
Sk*=![]()
![]()
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...





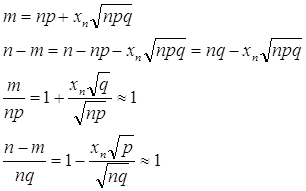
0 комментариев