Навигация
Дисперсия ДСВ и ее свойства
12. Дисперсия ДСВ и ее свойства
Математическое ожидание квадрата отклонения СВ от ее математического ожидания:
D(X) = M(x-M(X)2) = =(х1-М(Х))2р1+(х2-М(Х))2р2+....+(xn-М(Х))2рn .(2.3.2)
Свойства дисперсии:
1) D(С) = 0, где С=соnst;
2) D(CX)=C2D(X);
3) D(X)=M(X2)-(M(X))2, где М(Х2) = х21 р1 + x22 p2 + ...+ х2n рn;
4) Если СВ X и Y независимы, то D(X±Y)=D(X) + D(Y);
5) D(OX)=D(X);
6) Для любых СВ X и Y, D(X±Y)=D(X)+D(Y)±2cov(X,Y), где cov(X,Y)=M((X-mx)(Y-m )) - ковариация случайных величин X и Y (М(Х)= mx, M(Y)= m).
Дисперсия характеризует средний квадрат отклонения ДСВ, поэтому на практике часто используют в качестве характеристики разброса среднее квадратическое отклонение σ(Х)= √D(X) , которое имеет ту же размерность, что и СВ X.
Для биноминального закона
D(X)=npq, σ(X)=√npq;
для геометрического закона D(X)= q/p2;
для гипергеометрического D(X)=n(M/N)(1-M/N)(N-n)/(N-1);
для распределения Пуассона D(X)=λ.
Только для распределения Пуассона M(X)=D(X)= λ.
13. Показательное распределение.
НСВ X, принимающая неотрицательные значения, имеет показательное распределение, если ее дифференциальная функция имеет вид
![]()
где Я =const, Я >0.
Интегральная функция показательного закона с параметром λ:
![]()

Рис. Показательный закон
Если СВ X распределена по показательному закону, то:
1. Математическое ожидание М(Х) = 1/λ ;
2. Дисперсия D(X)=1/λ2, среднее квадратическое отклонение
σ(X)=√D=1/λ.
3. Вероятность попадания СВ X в заданный интервал определяется по формуле
Р(а≤х<b) = е-λа-е-λb.
Замечание. Показательное распределение играет большую роль в теории массового обслуживания (ТМО), теории надежности. В ТМО параметр X - среднее число событий, приходящихся на единицу времени. При определенных условиях число событий, произошедших за промежуток времени т, распределено по закону Пуассона с математическим ожиданием а =λτ. Длина промежутка t, между произвольными двумя соседними событиями, подчиняется показательному закону: P(T<t)=F(t)=l-eλt.
14. Закон распределения дискретной случайной величины
1. Биномиальный закон распределения. Случайная величина X принимает значения 0, 1, 2, 3, 4, 5,...,n, с вероятностью, определяемой по формуле Бернулли:
![]()
2. Закон распределения Пуассона. Случайная величина X принимает бесконечное счетное число значений: 0, 1, 2, 3, 4, 5,..., к,... , с вероятностью, определяющейся по формуле Пуассона:
![]()
где Х>0 - параметр распределения Пуассона.
![]()
При n→∞ и р→0 биномиальный закон приближается к закону распределения Пуассона, где λ, = np.
Геометрический закон распределения. Пусть Р(А)=р - вероятность наступления события А в каждом опыте, соответственно, q=l-p - вероятность не наступления события А.
Вероятность наступления события А в к-ом опыте определяется по формуле:
P(X=k)=p-qk-1. (2.2.2.)
Случайная величина X, распределенная по геометрическому закону принимает значения 1, 2,...,к,... , с вероятностью, определяемой по формуле (2.2.2):
![]()
4. Гипергеометрический закон распределения. Пусть в урне N-шаров, из них М белых, а остальные (N - М) черные. Найдем вероятность того, что из извлеченных n шаров m белых и (n-m) черных.
N= М + (N-M); n = m + (n-m);
СmM - число способов выбора m белых шаров из М;
Сn-mN-M- число способов выбора (n-m) черных шаров из (N-M).
По правилу произведения, число всех возможных наборов из m белых и (n-m) черных равно СmM Сn-mN-M;
CnN- общее число способов выбора из N шаров n.
Отсюда, по формуле классического определения вероятности, P(A)= (СmM Сn-mN-M)/ CnN
Ограничения на параметры: М≤N, m≤n; m = m0, m0 +1, m0+2,..., min(M,n), где m0=max{0, n-(N-M)}. Случайная величина Х, распределенная по гипергеометрическому закону распределения (при т=0,1,2,3,...,М), имеет вид:
![]()
Гипергеометрический закон определяется тремя параметрами N, М, n. При n<0,1N этот закон стремится к биномиальному.
Замечание.
1. В теории вероятностей различают две основные схемы: выбора элементов с возвращением каждый раз обратно и выбора без возвращения, которые описываются соответственно биномиальным и гипергеометрическим законами.
2. Геометрический закон описывает схему повторения опытов (в каждом из которых может наступить или не наступить событие А: Р(А)=р, q=l-p), до первого появления события А, то есть фактически это отрицательное биномиальное распределение при m=1.
16. Одинаково распределённые, взаимонезависимые дискретные случайные величины
СВ называют одинаково распределенными, если они имеют одинаковые законы распределения. Поэтому у них совпадают числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Пусть X1, Х2,..., Хn одинаково распределенные, взаимонезависимые ДСВ, тогда:
M(X1) = М(Х2) = ... = М(Хn) = М(Х), D(X1) = D(X2) = ...= D(Xn)=D(X).
Рассмотрим характеристики их средней арифметической X = (X1+X2+…+Xn)/n:

![]()
![]()
-стандартное отклонение СВ X.
Дисперсия относительной частоты (m/n) появления события А в n независимых испытаниях (в каждом из которых событие А появляется с вероятностью равной р, и не появляется с вероятностью q= 1-р; m-число появлений события А в серии из n испытаний), определяется по формуле
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...





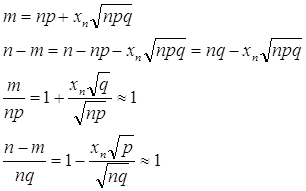
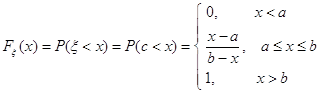
0 комментариев