Формула Симпсона

2.2 Формула Симпсона

Рассмотрим метод Ньютона-Котеса (т.е. ), в случае интерполяции подинтегральной функции квадратичными функциями на каждом интервале деления. В данном случае мы имеем дело с параболическим интерполированием, поэтому на каждом интервале , необходимо знание значения функции  в трёх точках (т.к.  имеет 3 неизвестных параметра – коэффициенты ). В качестве третьей точки на каждом отрезке  - выбирается середина этого отрезка, т.е. точка .

Вывод формулы Симпсона будем производить аналитически. Как и в предыдущем случае применяем интерполяционный многочлен Лагранжа, для интерполирования функции , на отрезке , при чём считаем, что нам известны значения . Тогда, очевидно, что многочлен Лагранжа имеет вид квадратичной функции:

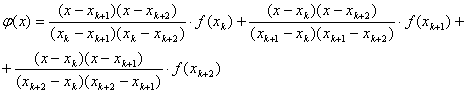 (15)

Интегрируя (15) на отрезке  будем иметь формулу:

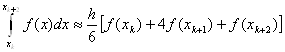(16)

используя свойство аддитивности интеграла, получаем:

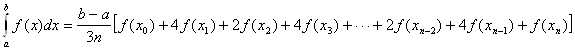(17)

где является четным числом (- число делений отрезка ,т.е. число равных отрезков разбиения).

Формула (17)-называется формулой Симпсона.

Приняв обозначения , получаем привычный вид квадратурных формул:

а) Формула трапеций:

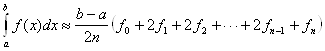(18)

б) Формула парабол (Симпсона) (при )

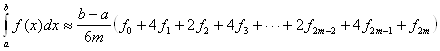(19)

2.3 Метод Ромберга

Пусть промежуток интегрирования разбит на  равных частей и для этого разбиения по формуле трапеции получено значение . Значение  - совпадает со значением вычисляемого интеграла, если интегрируемая функция  линейна, т.е. является многочленом первой степени. По формуле:

(20)

называемой формулой Ромберга, построим - схему:

(21)

Оказывается, что для интегрируемых по Риману функций, все столбцы и строки - схемы сходятся к исходному значению интеграла.

Пример: Выписать явные формулы для фрагмента - схемы:

Решение:

Пусть Тогда

Похожие работы

Метод наименьших квадратов в случае интегральной и дискретной нормы Гаусса

Скачать

7655

1

4

... отклонения Гаусса (10) по норме индуцированной скалярным произведением (15), действительно: (18) а дискретная норма Гаусса невязки имеет вид: (19) 2.2 Интегральное приближение функции  заданной аналитически   В предыдущем параграфе мы рассматривали приближение функции  методом наименьших квадратов, предполагая, что значения функции  заданы таблично, поэтому мы ...

Сущность метода Монте-Карло и моделирование случайных величин

Скачать

26423

6

2

... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...

Численное интегрирование определённых интегралов

Скачать

15012

2

23

... такое определённый интеграл. Возможны два различных подхода к определению определённого интеграла. ОПРЕДЕЛЕНИЕ 1: приращение F(b)-F(a) любой из преобразованных функций F(x)+c при изменении аргумента от x=a до x=b называют определённым интегралом от a до b функции f и обозначается . Причём функция F является первообразной для функции f на некотором промежутке D, а числа а и b принадлежат этому ...

Исследование точности численного интегрирования

Скачать

39882

6

11

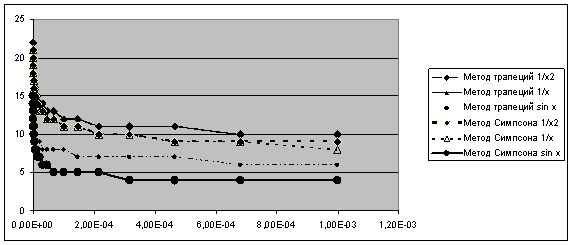
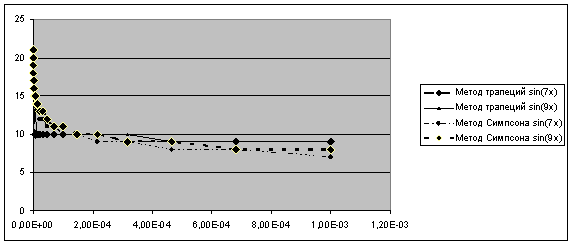
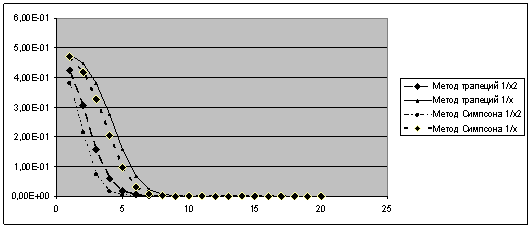
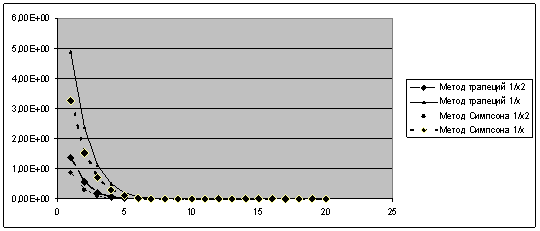
... и методика испытаний   5.1 Объект испытаний Объектом испытаний является программа, предназначенная для исследования внутренней сходимости численного интегрирования с помощью методов вычисления интегралов: методы трапеций и Симпсона.   5.2 Цель испытаний Целью испытаний является проверка точности работы программы для данной задачи.   5.3 Требования к программе Во время испытаний ...