Навигация
Квадратурные формулы Гаусса
3. Квадратурные формулы Гаусса
Во всех приведенных до сих пор формулах численного интегрирования Ньютона-Котеса и во всех формулах, получаемых методом Ромберга, используются равноотстоящие узлы. В случае квадратурных формул Гаусса это уже не так. Иначе говоря, смысл квадратурных формул Гаусса состоит в том, чтобы при наименьшем возможном числе узлов точно интегрировать многочлены наивысшей возможной степени. Можно показать, что при ![]() гауссовых узлах по полученной формуле можно точно интегрировать многочлены степени
гауссовых узлах по полученной формуле можно точно интегрировать многочлены степени ![]() .
.
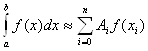 (22)
(22)
Для количества узлов и соответствующих значений ![]() и
и ![]() - составлены таблицы, которые позволяют вычислять интегралы по формуле (22).
- составлены таблицы, которые позволяют вычислять интегралы по формуле (22).
Для понимания сути этих таблиц рассмотрим пример.
Пример:
Пусть нам нужно составить квадратурную формулу с двумя узлами ![]() ,по которой точно интегрируются многочлены до
,по которой точно интегрируются многочлены до ![]() степень включительно.
степень включительно.
Решение: Искомая формула имеет вид:
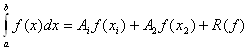 ,(23)
,(23)
где ![]() - остаток, который обращается в нуль, для
- остаток, который обращается в нуль, для
![]() , при
, при ![]() .
.
Тогда, подставляя в (23) имеем:
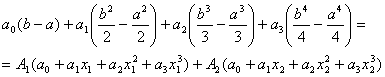 (24)
(24)
Отсюда, приравнивая коэффициенты при ![]()
![]() , справа и слева, получаем систему уравнений:
, справа и слева, получаем систему уравнений:
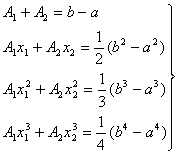 (25)
(25)
Ее решение имеет вид:
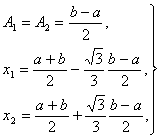 (26)
(26)
Следовательно, искомая квадратурная формула такова:
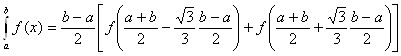 .(27)
.(27)
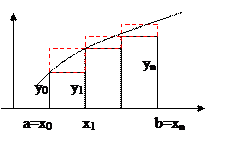
Ясно, что если нам нужно вычислить интеграл со многими узловыми точками, действуем следующим образом:
а) промежуток интегрирования ![]() делим на
делим на ![]() - равных промежутков и на каждом маленьком промежутке
- равных промежутков и на каждом маленьком промежутке ![]() применяем формулу Гаусса с неравноотстоящими узлами (27);
применяем формулу Гаусса с неравноотстоящими узлами (27);
б) полученные результаты складываем.
В случае, когда ![]() , оказывается, что узловыми точками при делении отрезка на
, оказывается, что узловыми точками при делении отрезка на ![]() - частей являются корни соответствующих многочленов Лежандра.
- частей являются корни соответствующих многочленов Лежандра.
Для вычисления кратных интегралов, их сводят обычно к повторным интегралам, а далее применяют те же самые кубатурные формулы для каждого значения узловых точек, что и в одномерном случае. Однако, надо иметь в виду, что кратные интегралы значительно сложнее вычислять с заданной точностью.
Точность произведённых вычислений зависит от точности аппроксимации подынтегральной функции многочленами.
4. Оценка интегралов
При численном интегрировании наряду с приближёнными формулами представляет также интерес нахождение нижних и верхних границ интегралов. Рассмотрим два метода оценки интегралов:
а) оценка интеграла в случае, когда подинтегральная функция ![]() , удовлетворяет условию:
, удовлетворяет условию:
![]() для
для ![]() (28)
(28)
б) общий случай.
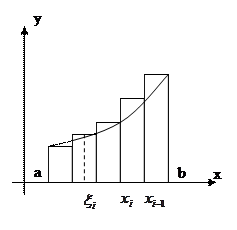
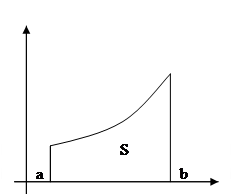
Рассмотрим интеграл:
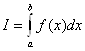 (29)
(29)
где ![]() ,
, ![]() . Не умоляя общность, будем считать, что
. Не умоляя общность, будем считать, что ![]() ,
, ![]() , тогда (Рис. 1) ясно, что
, тогда (Рис. 1) ясно, что
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
К Е
N
М
0 ![]()
![]()
![]()
![]()
Рис. 1
0 ![]()
![]()
![]()
![]()
Площадь криволинейной трапеции ![]() заключена между площадями aMNb и aKEb, т.е.
заключена между площадями aMNb и aKEb, т.е.
![]() (30)
(30)
Очевидно, что
![]() (31)
(31)
![]() (32)
(32)
Таким образом, для оценки интеграла в случае ![]() , имеем:
, имеем:
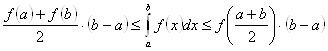 (33)
(33)
если же ![]() , неравенство (33) заменяется на обратное.
, неравенство (33) заменяется на обратное.
б) Другой принцип грубой, но зато общей оценки значения интеграла, основан на «монотонности» интеграла. При этом способе подынтегральную функцию приближают снизу и сверху интегрируемыми в замкнутом виде функциями ![]() и
и ![]() , т.е.
, т.е.
![]() ,
, ![]() (34)
(34)
Тогда
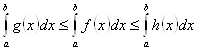 (35)
(35)
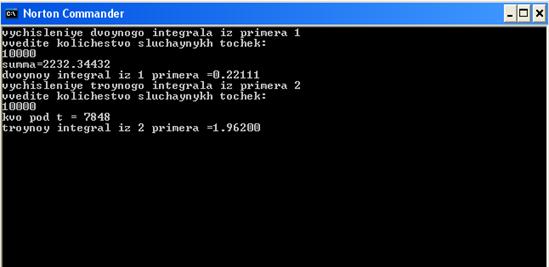
5. Вычисление интегралов методом Монте-Карло
Пусть нам нужно вычислить интеграл:
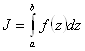 (36)
(36)
В случае, когда методы Ньютона-Котеса и Гаусса работают плохо, приходится обращаться к вероятностным методам случайного поиска. К таким методам относится метод Монте-Карло.
Для вычисления интеграла (36) методом Монте-Карло, заменим переменную интегрирования ![]() таким образом, чтобы пределы интегрирования
таким образом, чтобы пределы интегрирования ![]() отобразились соответственно в
отобразились соответственно в ![]() . Для этого нужно воспользоваться преобразованием:
. Для этого нужно воспользоваться преобразованием:
![]() (37)
(37)
тогда интеграл (36) принимает вид:
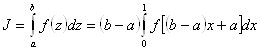 (38)
(38)
Для вычисления же интеграла на ![]() имеем формулу:
имеем формулу:
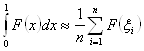 (39)
(39)
где ![]() - случайные числа, равномерно распределённые на
- случайные числа, равномерно распределённые на ![]() . Таким образом, по методу Монте-Карло, интеграл (36) считается по формуле:
. Таким образом, по методу Монте-Карло, интеграл (36) считается по формуле:
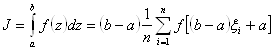 (40)
(40)
где ![]() - равномерно распределённые случайные числа из промежутка
- равномерно распределённые случайные числа из промежутка ![]() .
.
Аналогично, для кратных интегралов. Получаем:
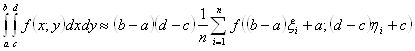 (41)
(41)
где ![]() - случайные точки, равномерно распределённые на квадрате
- случайные точки, равномерно распределённые на квадрате ![]() (Здесь знак «
(Здесь знак «![]() » означает декартовое произведение).
» означает декартовое произведение).
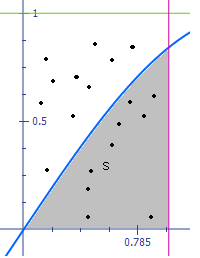
В случае, когда область интегрирования является сложным множеством ![]() (рис. 6), пользуемся прямоугольником
(рис. 6), пользуемся прямоугольником ![]() , который описывается вокруг множества
, который описывается вокруг множества ![]() . И интеграл по множеству
. И интеграл по множеству ![]() заменяем интегралом по прямоугольнику
заменяем интегралом по прямоугольнику ![]() , который уже умеем вычислять по формуле (41). Замена интеграла по множеству
, который уже умеем вычислять по формуле (41). Замена интеграла по множеству ![]() производится соотношением:
производится соотношением:
![]() (42)
(42)
где
![]() (43)
(43)
таким образом:
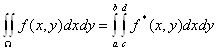 (44)
(44)
который легко рассчитывается по формуле (41).
Аналогично вычисляются и трёхкратные интегралы. Этот подход легко обобщается для n-кратных интегралов.
Литература
1. Р.В. Хемминг. Численные методы, Наука, М.,1998
2. Коллатц., Ю.Альбрехт. Задачи по прикладной математике. Мир, М.,1998.
3. Т.Шуп. Решение инженерных задач на ЭВМ. Мир, М., 1992.
4. К.Бреббия, Ж. Теллес, Л. Врубел.Методы граничных элементов. Мир, М.,1987.
5. И.С.Берехин., Н.П.Жидков. Методы вычислений, ч.1., М.,1982.
Похожие работы
... отклонения Гаусса (10) по норме индуцированной скалярным произведением (15), действительно: (18) а дискретная норма Гаусса невязки имеет вид: (19) 2.2 Интегральное приближение функции заданной аналитически В предыдущем параграфе мы рассматривали приближение функции методом наименьших квадратов, предполагая, что значения функции заданы таблично, поэтому мы ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...
... такое определённый интеграл. Возможны два различных подхода к определению определённого интеграла. ОПРЕДЕЛЕНИЕ 1: приращение F(b)-F(a) любой из преобразованных функций F(x)+c при изменении аргумента от x=a до x=b называют определённым интегралом от a до b функции f и обозначается . Причём функция F является первообразной для функции f на некотором промежутке D, а числа а и b принадлежат этому ...
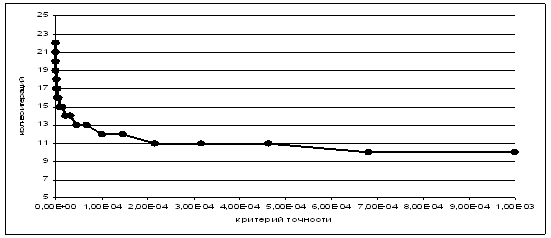
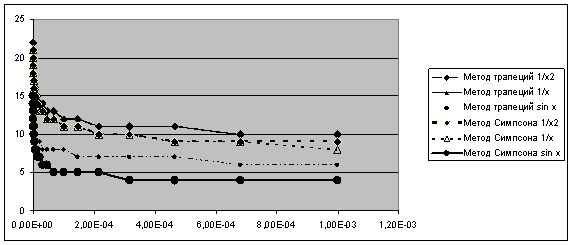
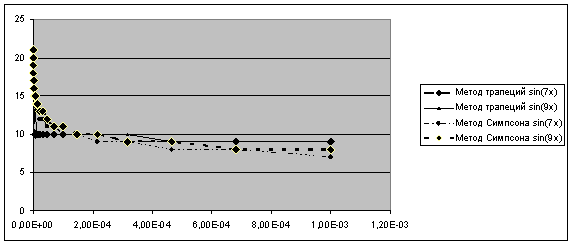
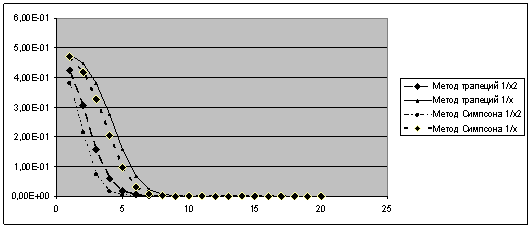
... и методика испытаний 5.1 Объект испытаний Объектом испытаний является программа, предназначенная для исследования внутренней сходимости численного интегрирования с помощью методов вычисления интегралов: методы трапеций и Симпсона. 5.2 Цель испытаний Целью испытаний является проверка точности работы программы для данной задачи. 5.3 Требования к программе Во время испытаний ...


0 комментариев