РОЗРОБКА МОДЕЛІ СИСТЕМИ КЕРУВАННЯ ЕЛЕКТРОПЕРЕДАЧІ ДИЗЕЛЬ-ПОТЯГУ

2. РОЗРОБКА МОДЕЛІ СИСТЕМИ КЕРУВАННЯ ЕЛЕКТРОПЕРЕДАЧІ ДИЗЕЛЬ-ПОТЯГУ

2.1. Моделювання тягових двигунів дизель-потягу

Даний розділ присвячено питанням розробки математичної моделі системи керування енергетичної системи дизель-потягу з тяговими асинхронними двигунами та їхній технічній реалізації з використанням комп’ютерних та інформаційних технологій. Серед розглянутих моделей приведені результати розробки моделей тягових двигунів з урахуванням їхнього використання для рішення задач синтезу регуляторів та дослідження об’єкту в цілому, моделей пристроїв формування керуючих впливів для випадків представлення ТАД у нерухомій двохфазній та трифазній системі координат, моделей регуляторів САК, системи керування та їхніх функціональних схем із врахуванням технічної реалізації, результати дослідження моделей та визначення адекватності.

У якості тягового асинхронного двигуна в системі, що моделюється, приймається ідеалізована машина з симетричною системою обмоток статора і ротора, гладким повітряним зазором, синусоїдальним розподілом магнітного потоку уздовж окружності статора і ротора, при роздільному обліку насичення по головному шляху магнітного потоку та по шляхам розсіювання, без урахування ефекту витіснення струму в обмотках ротора та втрат сталі [25].

Об’єкт дослідження в загальному вигляді може бути представлений системою диференційних рівнянь, що описують електромагнітні процеси ТАД як у прямокутній системі координат α, β, так і в природній (в осях a,b,0) [26].

Математична модель електроприводу у нерухомій прямокутній системі координат у осях α і β описується системою диференціальних рівнянь (2.1), що приведені нижче [26, 27].

 (2.1)

де , , , , ,  - відповідно проекції на вісі координат α і β потокозчеплення, напруги та струму обмоток статора;

, , ,  - відповідно проекції на вісі координат α і β потокозчеплення та струми обмоток ротора;

, , , , ,

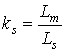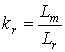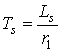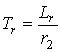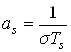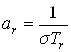,; , , , , ,  - постійні коефіцієнти для даного типу ТАД.

Струми , , ,  визначаються через потокозчеплення , , ,  наступним чином:

; ; ; .

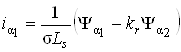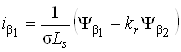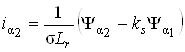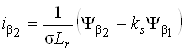Момент опору навантаження М_с у залежності від частоти  може бути представлений у вигляді лінійної залежності, що визначається виразом:

(2.2)

або нелінійної залежності:

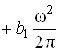 , (2.3)

де a₀, b₀, b₁ – постійні величини.

Використання рівнянь у нерухомій системі координат та врахування несинусоїдальної форми напруги живлення ТАД призводить до надмірної громіздкості рівнянь та складності математичної моделі, однак дозволяє проводити дослідження з урахуванням миттєвих значень змінних станів, що в ряді випадків є необхідним при дослідженні явищ, що притікають в системах електропривода. Тому для якісних досліджень на ПЕОМ доцільно використовувати метод огинаючої, запропонований О.О.Булгаковим [27, 28]. При цьому для запису рівнянь використовується система ортогональних осей X, Y, що обертаються синхронно зі швидкістю результуючого вектора напруги (струму) статора. Цей метод годиться для обмеженої області частот, коли пульсаціями швидкості двигуна, які зумовлені несинусоїдальністю напруги, можна знехтувати.

Рівняння асинхронного двигуна в синхронній системі координат X, Y мають вигляд [27, 26]:

(2.4)

де  - кутова частота напруги статора двигуна при p = 1;

, , , , ,  - відповідно проекції на осі X₁ та Y₁, X₂ та Y₂ потокозчеплень статора і ротора та напруги живлення; всі інші змінні були описані вище.

Напруги по осям X, Y (функції впливу) визначаються наступними рівняннями для випадку синусоїдальних напруг на статорі двигуна:

 = U_M cos [(W₀ – W_K)t + j_K],

 = U_M sin [(W₀ – W_K)t + j_K],

де U_М - амплітуда першої гармоніки фазної напруги на статорі двигуна;

 - кутова швидкість обертання осей координат;

 - довільна початкова фаза напруги обмотки А статора.

У випадку синхронних осів  за умови, що початкова фаза напруги , функції впливу – це постійна напруга, яка дорівнює U_M по осі X, та нульова напруга по осі Y.

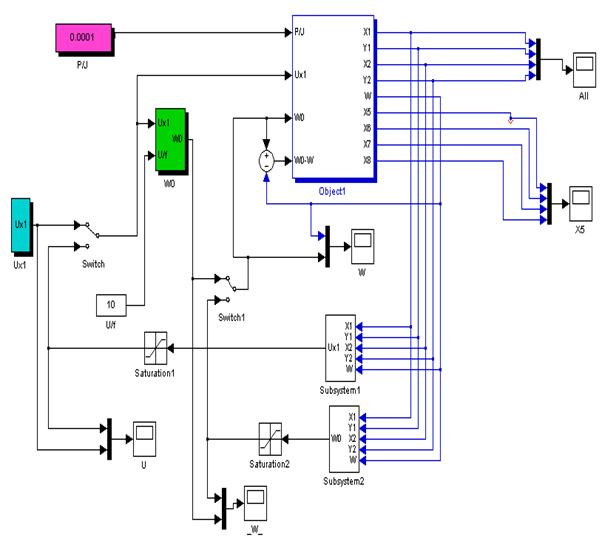
Рис.2.1. Структурна схема моделі в пакеті MatLab.

На рис. 2.1 приведена структурна схема моделі, що реалізує систему рівнянь (2.4) у пакеті MathLab. Вона складається з наступних частин: блока формування сигналів керування(функцій впливів) по амплітуді  (Subsystem1) та частоті w₀ (Subsystem2); блока інтегрування системи диференційних рівнянь (2.4) у вигляді субблока Object1; блока задавання похідних даних та параметрів ТАД; блока обмеження амплітуди та частоти напруги сигналу керування та ряду допоміжних блоків (перемикачів – Switch); блока, який задає певне співвідношення між амплітудою напруги та частотою (один з таких законів управління U/f = const); блоків відображення інформації.

Вхідними сигналами для субблока моделі Object1 є сигнали, пропорційні керуючим впливам  и w₀, а вихідними сигнали – потокозчеплення (X₁, Y₁, X₂, Y₂), струми (X₅ – X₈) ТАД та кутова швидкість крутіння ротора двигуна в залежності від моменту навантаження, що визначається моментом інерції J. У математичній та машинній моделях мають місце наступні відповідності:

 º X₁;  º Y₁;  º X₂;  º Y₂.

Змінні X₅ – X₈ - проекції струмів статорної та роторної обмоток ТАД на відповідні осі координат.

На рис. 2.2 і 2.3 приведені перехідні процеси у вигляді осцилограм, що демонструють роботу моделі при визначених початкових умовах у замкненій системі керування (сигнали керування формуються або згідно до певного закону, наприклад U/f = const, або згідно до заданого закону керування, синтезованого з використанням змінних стану об’єкту). На рис. 2.4 приведені процеси, відповідні сигналу задавання w₀ та сигналу w, відповідної швидкості обертання ротора ТАД при визначених заданих умовах розгону та відповідних параметрах ТАД, який являє собою деяку інтегральну характеристику розглянутого об’єкта керування.

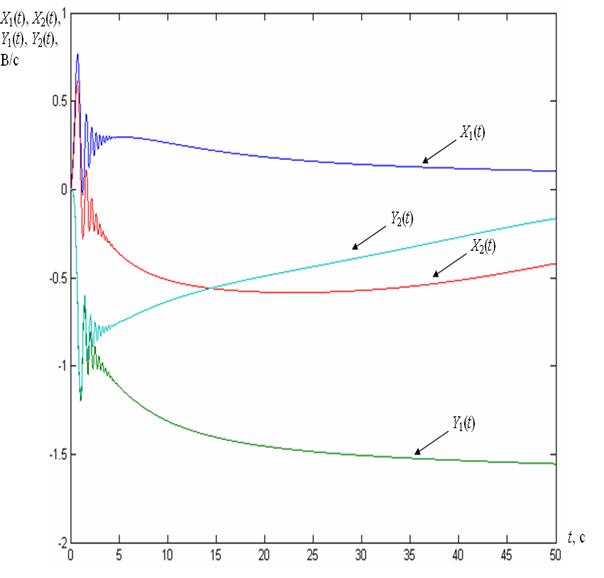
Рис. 2.2. Залежності X₁(t), Y₁(t), X₂(t), Y₂(t).

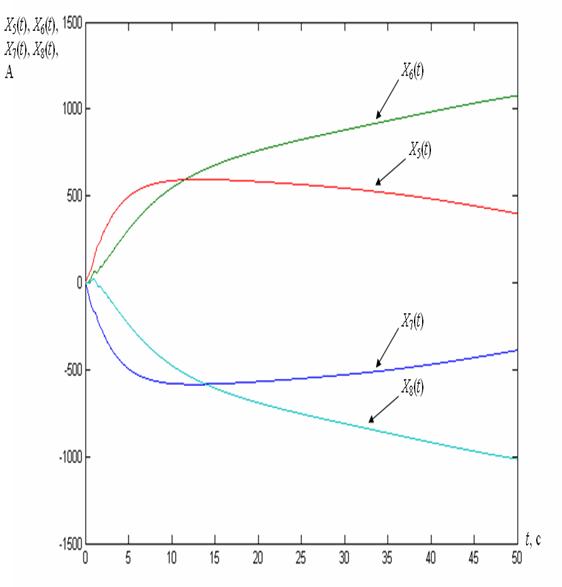
Рис. 2.3. Залежності X₅(t), X₆(t), X₇(t), X₈(t).

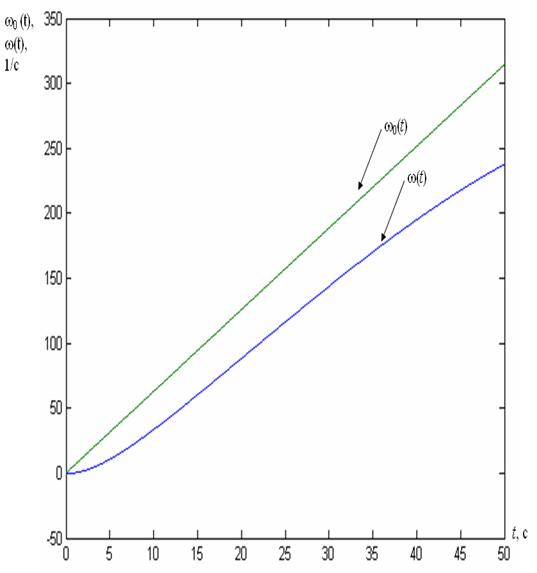
Рис. 2.4. Залежності w₀(t), w(t).

Ряд експериментів, проведених з моделлю, підтвердили її адекватність, що й дозволило зробити висновок про те, що запропонована модель в осях X, Y,0 може бути використана для проведення досліджень та синтезу керуючих впливів у вигляді амплітуди і частоти напруги живлення ТАД. Крім того, вона може бути використана для уточнення структур САК, що вже маються, та розробки структур САК на основі синтезованих законів керування згідно заданих критеріїв якості, а також визначення та уточнення параметрів САК по результатам досліджень. Особливо вона корисна для попередньої оцінки параметрів регуляторів, які синтезуються для системи керування.

Для проведення комплексних досліджень синтезованих систем управління може бути використана модель ТАД у фазних координатах a, b, 0 зі врахуванням насичення, яка представлена у вигляді системи рівнянь:

,

,

, (2.5) ,

де  – відповідно потокозчеплення, напруга та струм фаз a та b статора;

 – потокозчеплення та струм обмоток фаз a та b ротора;

 – модуль вектора струму, який намагнічує;

 –електромагнітний момент ТАД.

Відповідність вище приведених параметрів між собою має вигляд:

; ; ; ; ; ; ; ; ; ; ; ; ;

.

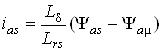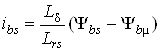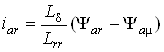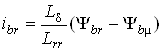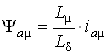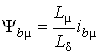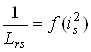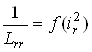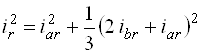Математична модель ТАД, що представлена у вигляді рівнянь (2.5), більш складна, ніж моделі вигляду (2.1) і (2.4), оскільки тут ряд параметрів є постійними величинами, як у попередніх моделях, а являють собою функції модуля вектору току, що намагнічує.

Аналіз моделей, що задані системами рівнянь (2.1) – (2.5), показує, що в залежності від мети досліджень, кожна з них може біти використана для визначення керуючих впливів.

Аналіз різних форм запису показує, що для моделювання безпосередньо двигуна та механізму, без урахування властивостей джерела живлення (приймаємо його джерелом ЕРС), найбільш проста модель виходить при запису рівнянь двигуна в рухомій системі координат в осях X,Y через потокозчеплення. Моделювання ТАД як у прямокутній системі координат a, b, так і у природній (в осях a,b,0) доцільно використовувати для дослідження об’єкту керування у замкненій системі регулювання з урахуванням протікання електромагнітних процесів.

Похожие работы

Системи підтримки прийняття рішень в економіці

Скачать

76071

1

6

... інші території. На додаток до цього моделі прогнозування в СППР та основані на реальних знаннях системи часто використовуються як настільні, розраховані на одного користувача системи. Системи підтримки прийняття рішень набули широкого застосування в економіках передових країн світу, причому їхня кількість постійно зростає. На рівні стратегічного управління використовується ряд СППР, зокрема для ...

Прогнозування розвитку динаміки України як господарської системи

Скачать

57417

2

12

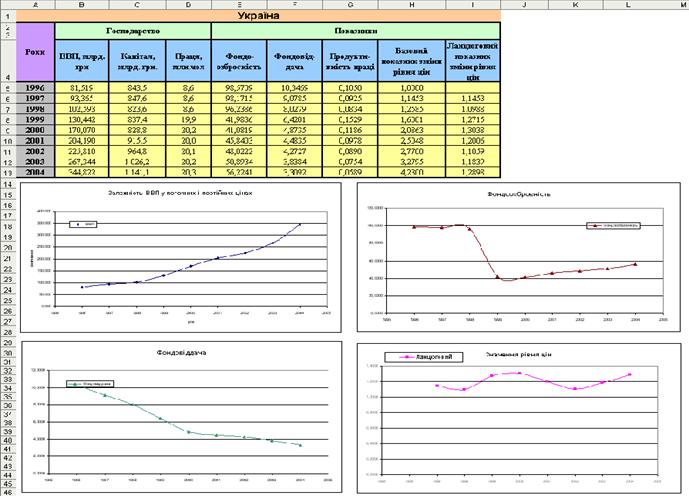
... періоді. Цей прогноз після Кабінету Міністрів України його головних показників є орієнтиром для підготовки пропозицій про визначення економічної політики на середньостроковий період. 3. ПРОГНОЗУВАННЯ РОЗВИТКУ ДИНАМІКИ УКРАЇНИ ЯК ГОСПОДАРСЬКОЇ СИСТЕМИ Порядок виконання роботи: а) Введення вихідних даних і одержання похідних рядів. Ввів в таблицю часові ряди, що відповідають вихідним даним ...

Дослідження надійності твердосплавних пластин для токарних різців з надтвердих матеріалів

Скачать

33705

0

0

... різця й шорсткості обробленої поверхні; - розробити методику оцінки й визначити ймовірність руйнування різців, які оснащені круглими алмазно-твердосплавними пластинами. Об'єкт досліджень – процес чистового та напівчистового точіння силумінів різцями, які оснащені АТП. Предмет досліджень – надійність інструментів з алмазних композиційних НТМ на прикладі АТП, реєстрація та аналіз сигналів АЕ. ...

Інформаційна система "Облік мобільних терміналів"

Скачать

67019

4

10

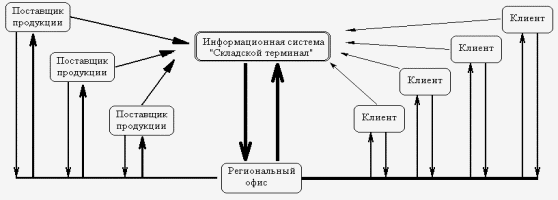
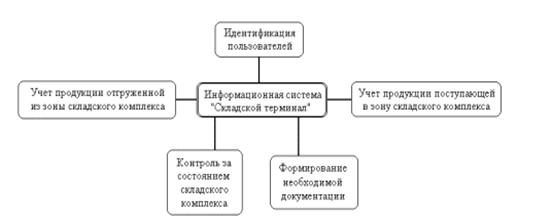
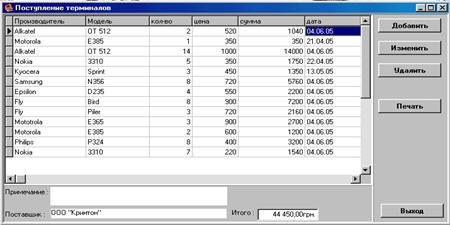
... , хоча воно й може змінюватися при зміні інформації, що зберігається в базі даних. 2.4 Опис програми, форм, звітів Файлом, що запускає інформаційну систему «Облік мобільних терміналів» є здійсненний файл PR.EXE. Розглянемо дії користувача при роботі з системою. Оператор системи обліку і аналізу розрахунків з постачальниками (менеджер) запускає програму на виконання (виконувальний файл PR.exe ...