Требования к содержанию программ элективных курсов
Учебное пособие для учащихся
Количество корней квадратного трехчлена
Организационный момент. Сообщение темы и целей занятия
Решение задач. Задание 1 решает один из учеников на доске. Затем ученики выполняют задания самостоятельно с последующей проверкой на доске
Выполнение заданий в парах
При каком значении параметра а корни трехчлена
Закрепление полученных знаний
Организационный момент
Закрепление полученных знаний
Решение отобранных учителем задач из №2 домашнего задания
Проверка уровня знаний, умений и уровня познавательной самостоятельности учащихся
Подведение итогов урока
Навигация
При каком значении параметра а корни трехчлена
Элективный курс по алгебре для 9-го класса на тему "Квадратные уравнения и неравенства с параметром"
87023
знака
7
таблиц
1
изображение
2. При каком значении параметра а корни трехчлена
3х2+(а
-4а)х+а-1 равны по модулю и противоположны по знаку?
3. Найти все значения а, при которых имеет корни уравнение
(2а+1)х-3(а+1)х+(а+1)=0.
4. При каком значении а уравнения х2+ах+1=0 и х2+х+а=0 имеют общий корень?
5. При каких значениях параметра р сумма квадратов корней уравнения х2+(р-1)х+р-1,5=0 наибольшая?
6. Найти наименьшее значение выражения х12 + х22, если х1 и х2 – корни уравнения х2 - 2ах + а + 6 = 0.
7. Корни х1и х2уравнения х2+рх+12=0 обладают свойством х2-х1=1. Найти р.
8. При каком значении а уравнение (а+4х-х-1)(а+1-
)=0 имеет 3 корня?
4. Подведение итогов занятия:
- Подсчет количества верно решенных заданий у каждой команды, начисление командам баллов.
- Определение уровня достижения целей урока и меру участия каждого учащегося в занятии, оценка работы школьников. В каждой группе заполняется таблица (Таблица 4), происходит распределение общего количества баллов между членами каждой команды.
5. Постановка домашнего задания:
Каждый ученик должен выполнить любые пять заданий из блоков 1 и 2, которые не решал на занятии.
Литература: [3], [4], [5], [8], [9], [12], [13], [16], [18], [25], [29], [32], [33].
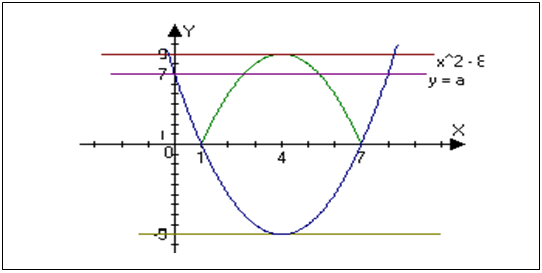
Занятие V. Расположение параболы относительно оси абсцисс
Цели: рассмотрение возможных случаев расположения параболы относительно оси абсцисс; использование графических представлений при решении задач; применение имеющихся знаний по решению квадратного уравнения.
Ход занятия:
1. Организационный момент.
2. Актуализация имеющихся знаний и мотивация изучения нового материала.
График квадратичной функции 
– парабола, вершина которой находится в точке с координатами (-B/(2A); -D/(4A)).
Ученикам дается задание самостоятельно изобразить все возможные случаи расположения параболы относительно оси Ох. Затем один из учеников изображает эти варианты на доске.
Возникают вопросы: Как задать нужное расположение параболы? Каким условиям должны удовлетворять коэффициенты параболы, чтобы она была определенным образом расположена относительно оси Ох?
3. Изучение нового материала.
Происходит беседа по изображенным рисункам, в результате которой составляется таблица (Таблица 5).
Таблица 5
| 1. |
| 2. |
| 3. |
|
| 4. |
| 5. |
| 6. |
|
Похожие работы
... -иллюстративного и репродуктивного метолов, а экономический профиль ориентирован на формирование прикладного стиля мышления. 2. Методика проведения элективных курсов по математике в профильной школе 2.1 Цели организации элективных курсов по математике Принципиальным положением организации школьного математического образования в настоящее время является дифференциация обучения ...
... на уроках алгебры и занятиях элективного курса по математике, участие проектной группы в городской конференции по данной теме в 2006 году. Объектом исследовательской работы было решение уравнений с параметрами, связанных со свойствами выше представленных функций. Структура данной работы включает в себя теорию, практическую часть, заключение, библиографический список. Решение уравнений с ...
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... Этим числам соответствуют три точки: A (), B () и C (). Они расположены на единичной окружности и делят ее на три равные части (рис. 18). Рис. 18. Задача 42. Изобразите на плоскости комплексные числа , удовлетворяющие условию: . Решение , значит, и . Получили две точки: B () и C () (рис. 19). Рис. 19. Задача 43. Изобразите множество точек комплексной плоскости, удовлетворяющих условию: ...
0 комментариев